Regressionsanalyse
_Statistik
TH Deggendorf
22.04.2025
Einleitung
Beispiele für lineare Beziehungen
Können wir uns die folgenden Je-Desto-Abängigkeiten vorstellen?
- Gewicht einer Person in Abhängigkeit von ihrer Größe
- Studienerfolg in Abhängigkeit von der Abiturnote
- Spritverbrauch eines PKW in Abhängigkeit von seiner Leistung
- Geschwindigkeit enzymatischer Reaktionen in Abhängigkeit von der Enzymkonzentration
- Bildungsstand einer Person in Abhängigkeit vom sozioökonomischen Status der Eltern
- Einkommen einer Person in Abhängigkeit von der Intelligenz
- Wohlgeschmack von Kaffee in Abhängigkeit von der Zuckerkonzentration
- Lebenszufriedenheit in Abhängigkeit vom Einkommen
Begriffe
- Einfaches lineares Regressionsmodell für einen Prädiktor: \(y = b_0 + b_1x_1 + \epsilon\)
- Multiples lineares Regressionsmodell für n Prädiktoren: \(y = b_0 + b_1x_1 + b_2x_2 + \dots +\,b_nx_n + \epsilon\)
- … für n Prädiktoren ohne Residuen: \(\hat{y} = b_0 + b_1x_1 + b_2x_2 + \dots +\,b_nx_n\)
- \(x\): Prädiktor, unabhängige Variable (UV), Regressor
- \(y\): Kriterium, abhängige Variable (AV), Regressand; tatsächliche Kriteriumswerte
- \(\hat{y}\): Schätzung/Vorhersage von \(y\) durch das Modell; geschätzte Kriteriumswerte
- \(\epsilon\): \((= y - \hat{y})\); Residuum/Residuen; d. h. Abweichung/en zwischen Modell(prognosen) und tatsächlichen Daten
- \(b_0, \dots, b_n\): Parameter des linearen Modells; Regressionsgewichte
- \(b_0\): Wert der AV, wenn alle UV = 0
Einfache lineare Regressionsanalyse, visueller Zugang
Zweidimensionale Daten \(y \sim x\)
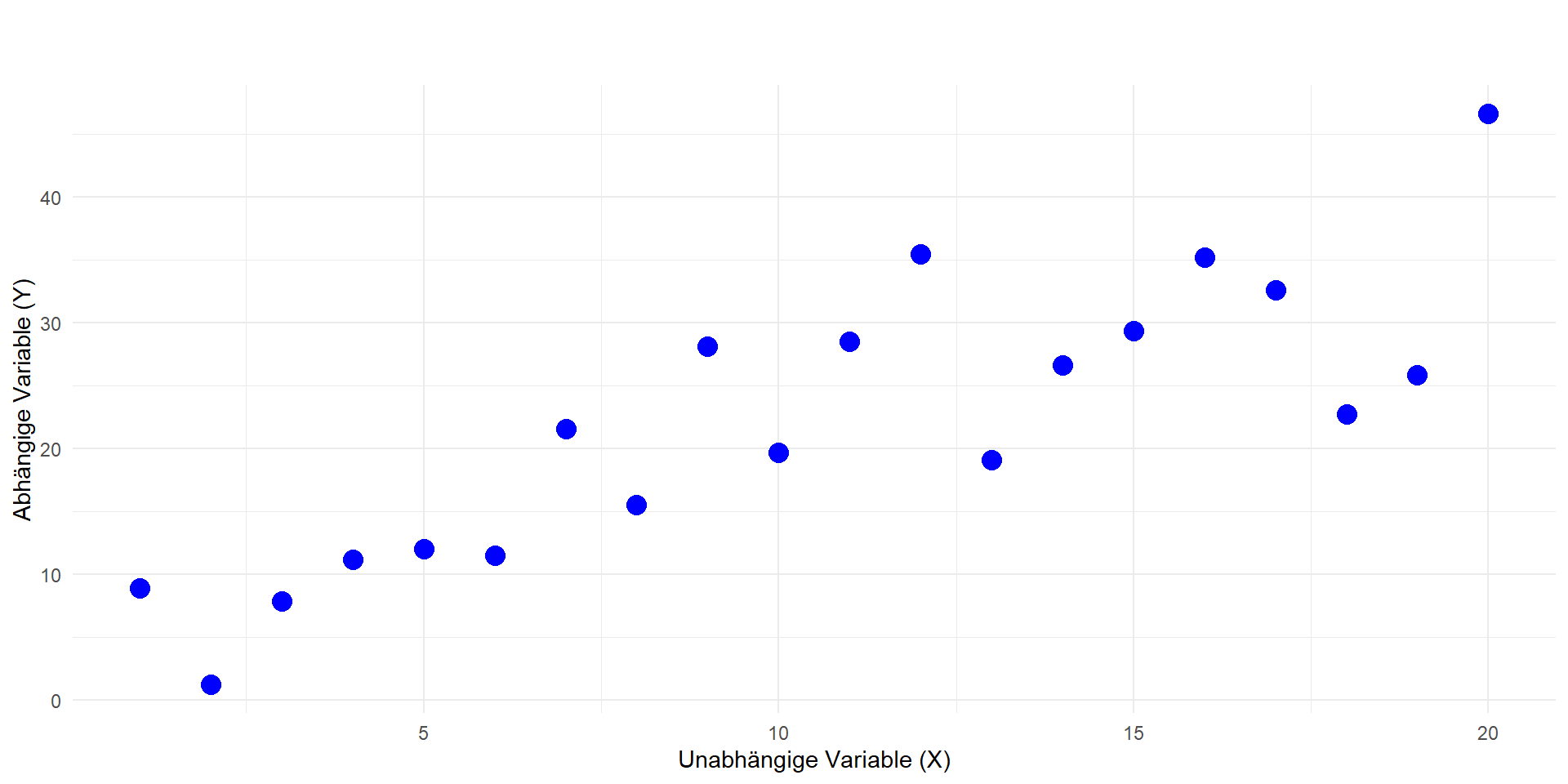
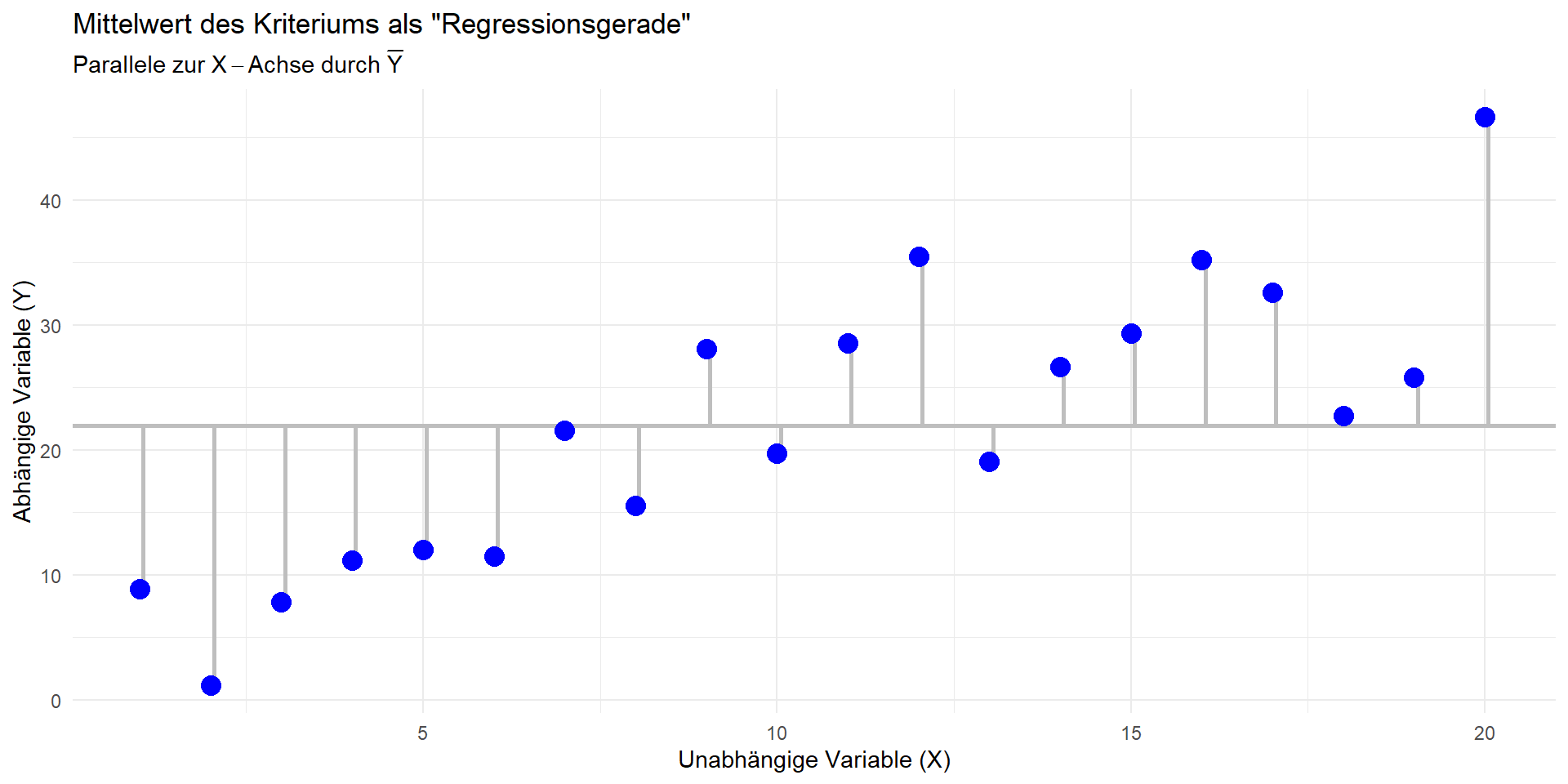
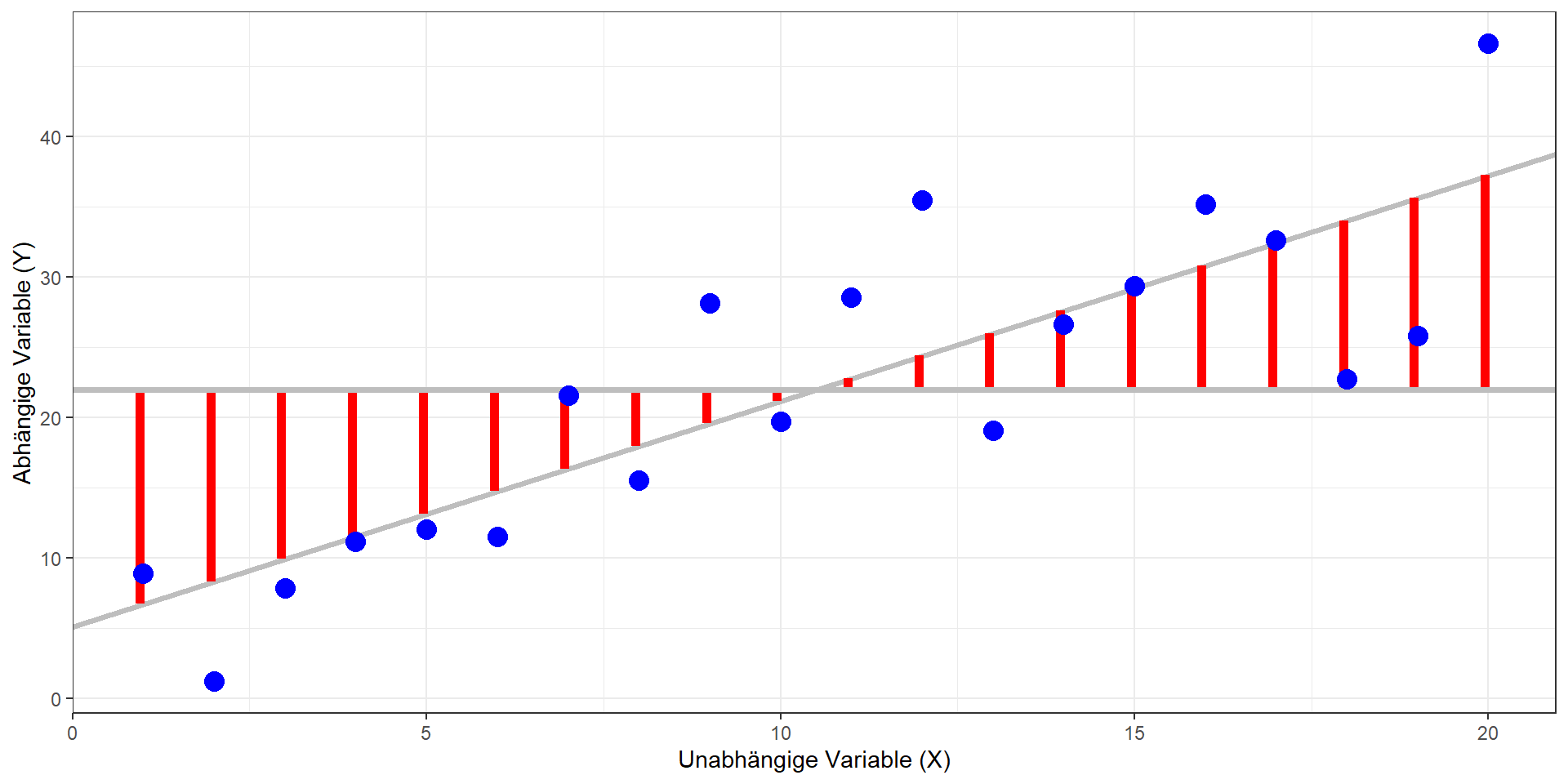
“Nullmodell”: \(b_1 = 0 \Rightarrow \hat{y}=\bar{y}\)
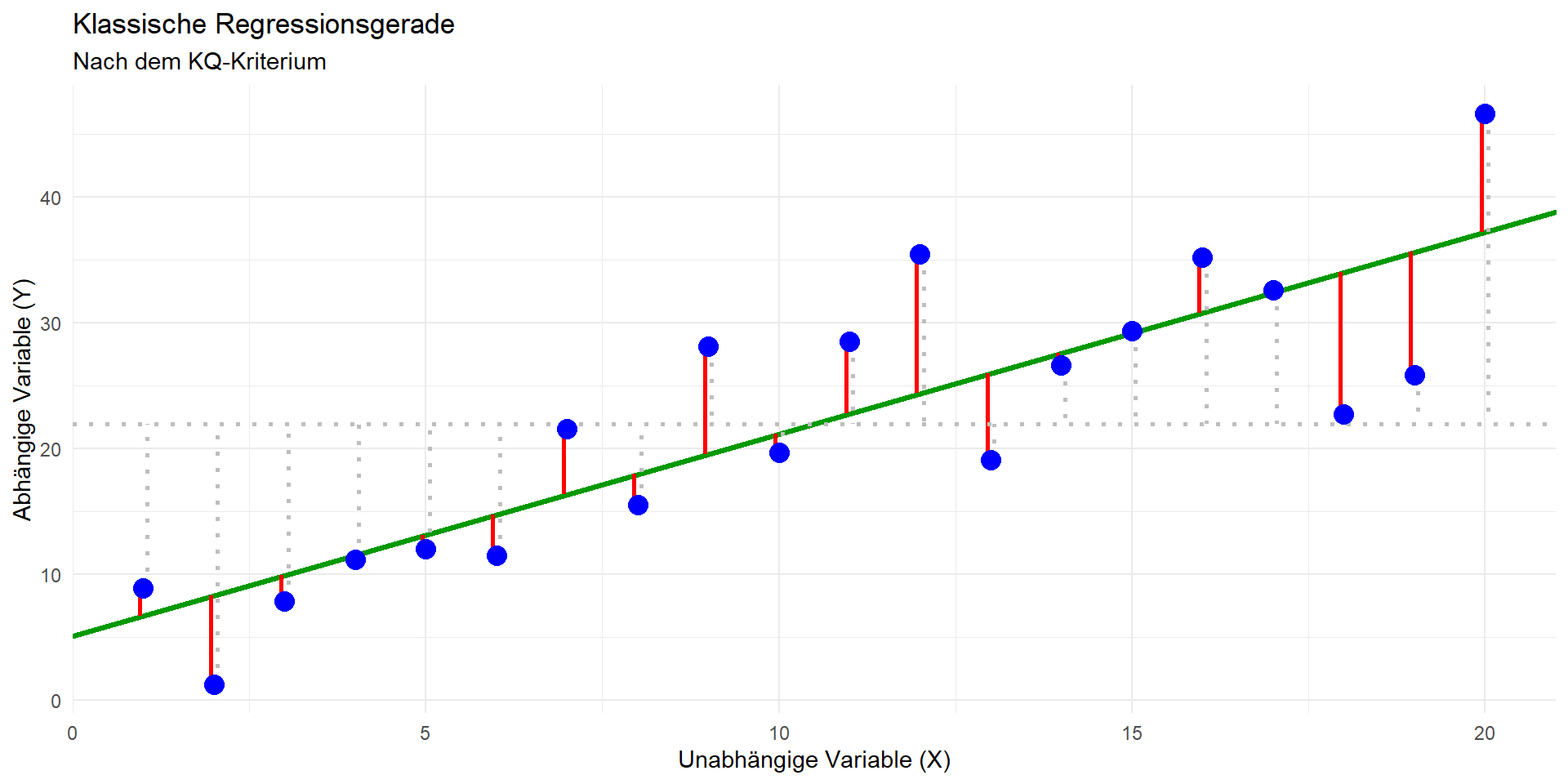
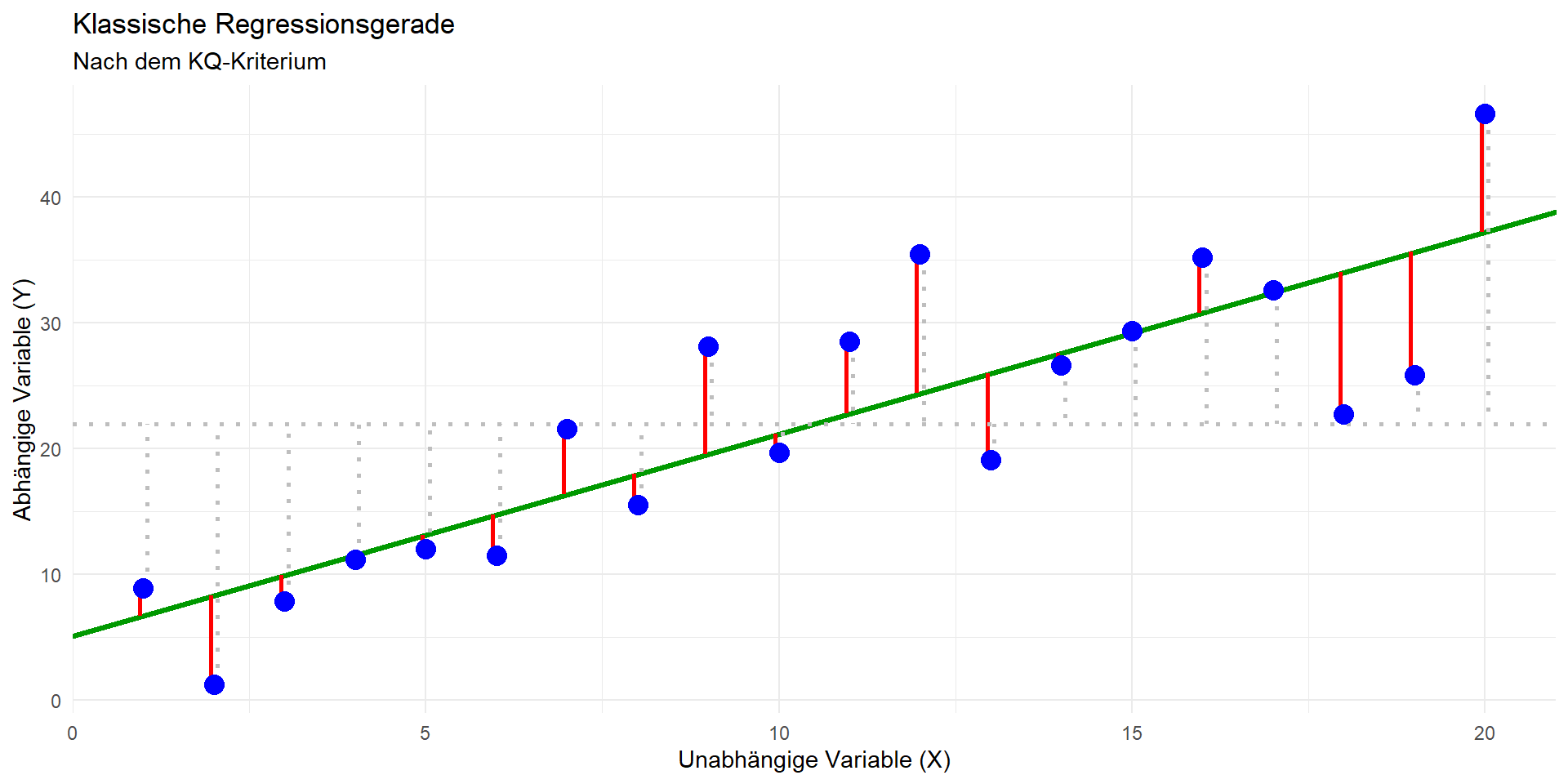
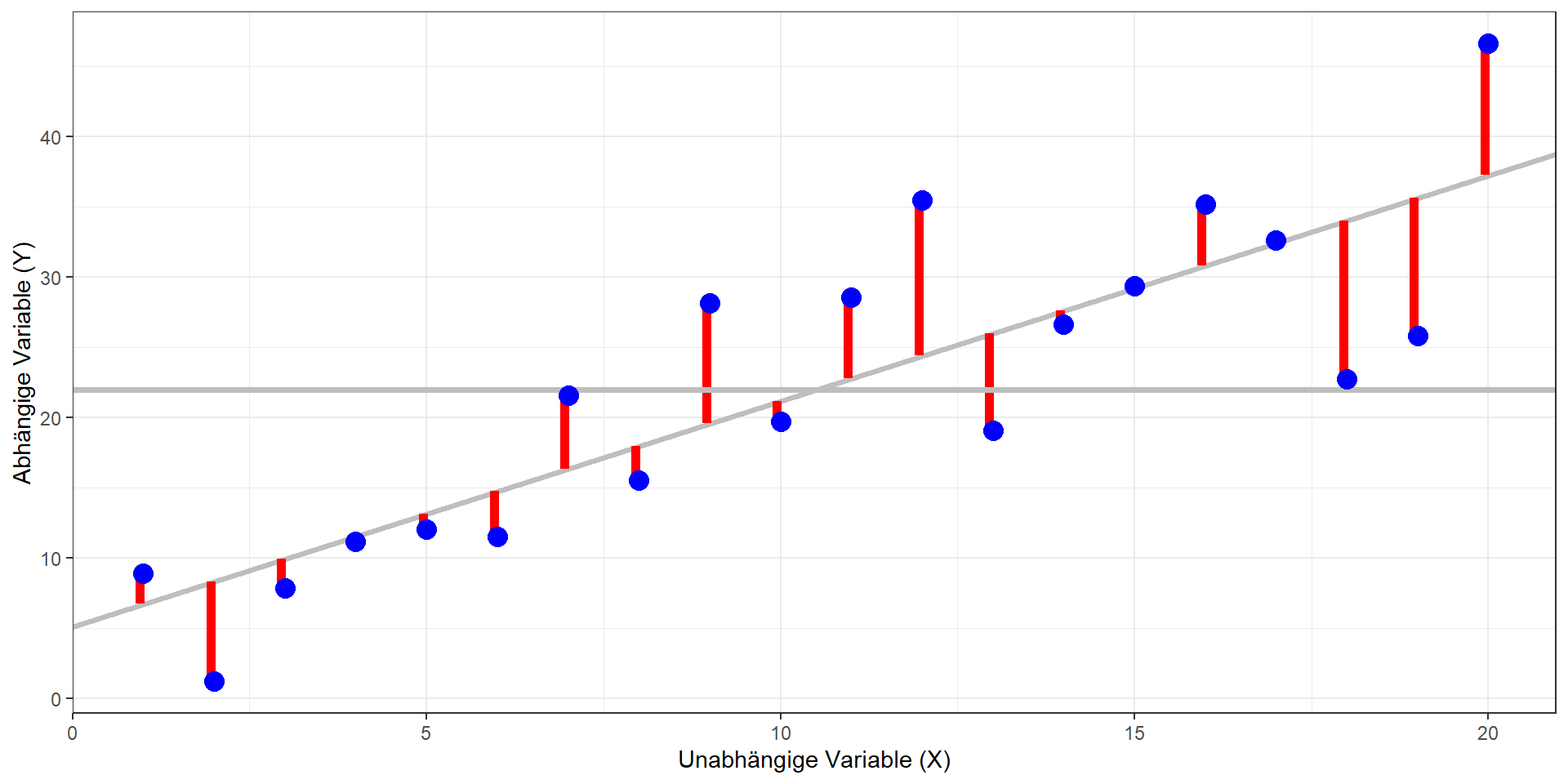
Regressionsmodell: \(\hat{y} = b_0 + b_1x_1\)
KQ, Quadratsummen & Signifikanztest
Methode der kleinsten Quadrate
- Modell: \(\hat{y} = b_0 + b_1x_1\)
- Ziel: Bestimmen einer Geraden, die die quadrierten vertikalen Abstände der Datenpunkte vom Modell minimiert (= Residuen; in der Grafik rechts die roten Linien)
- Bestimmung der Modellparameter:
- Geradensteigung \(b_1 = r \cdot \hat{\sigma}_y/\hat{\sigma}_x\)
- Achsenabschnitt \(b_0 = \bar{y} - \bar{x} \cdot b_1\)
Totale Quadratsumme: \(QS_{tot}\)
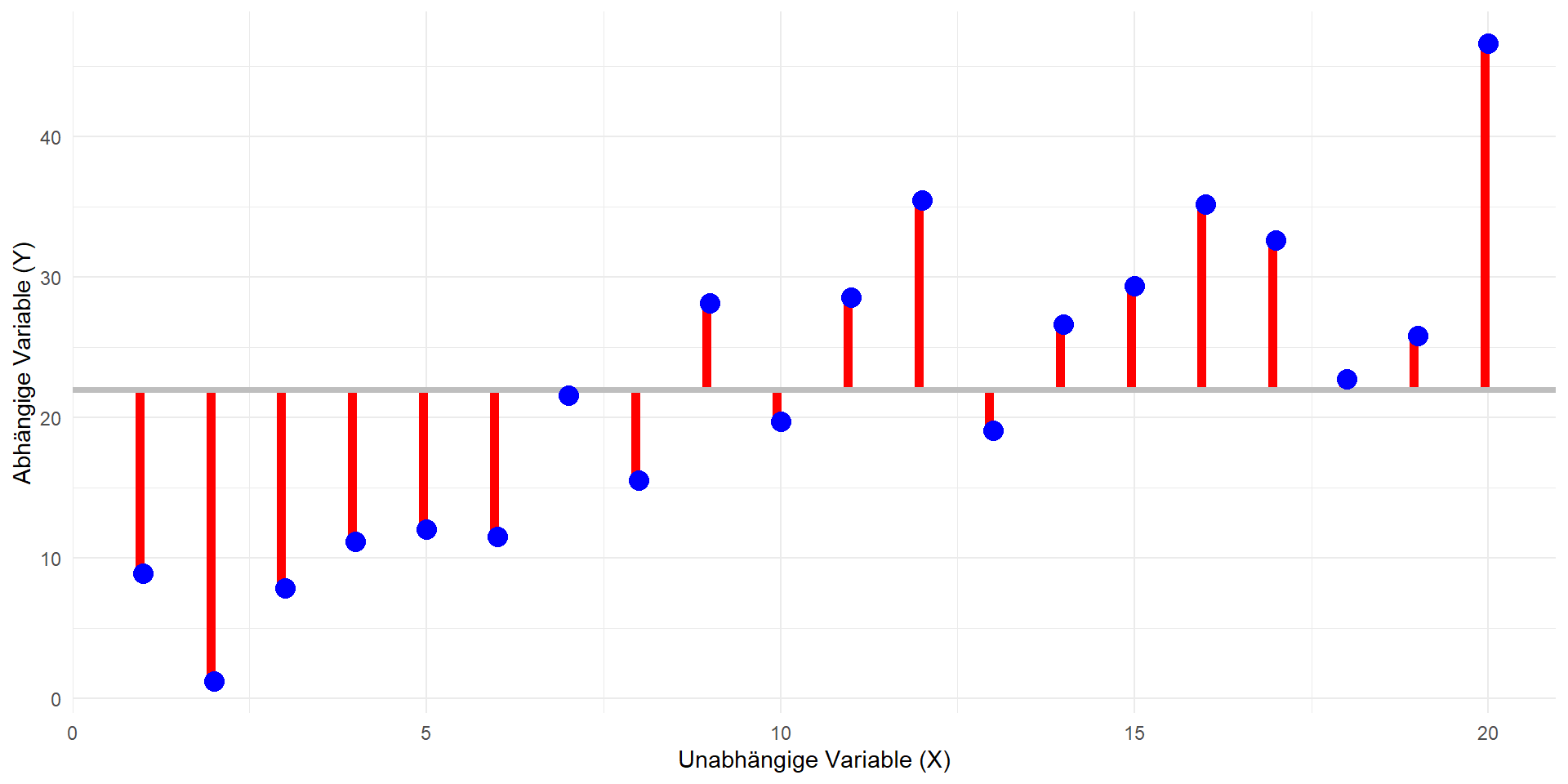
Modell-Quadratsumme: \(QS_{mod}\)
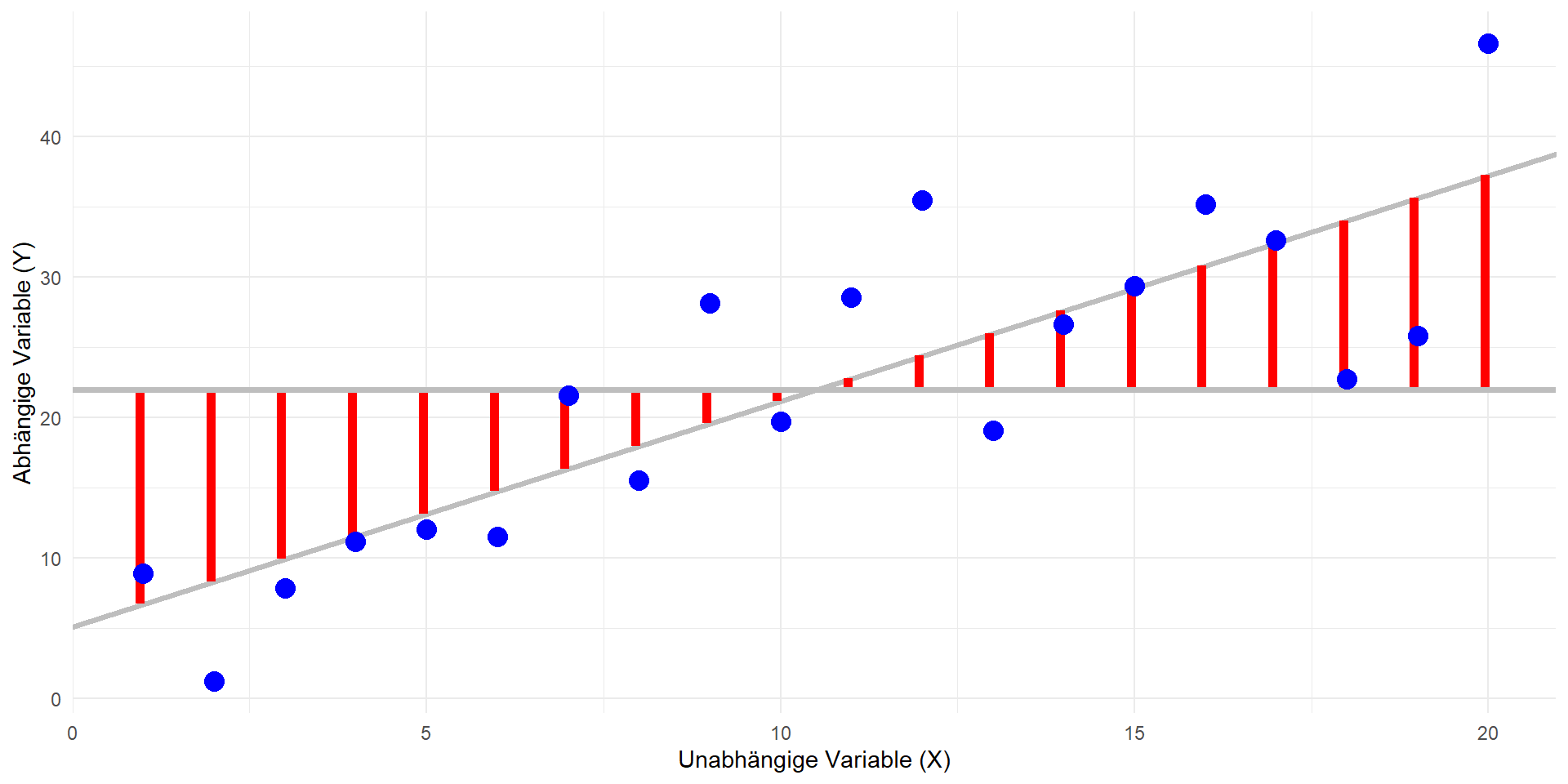
Residual-Quadratsumme: \(QS_{res}\)
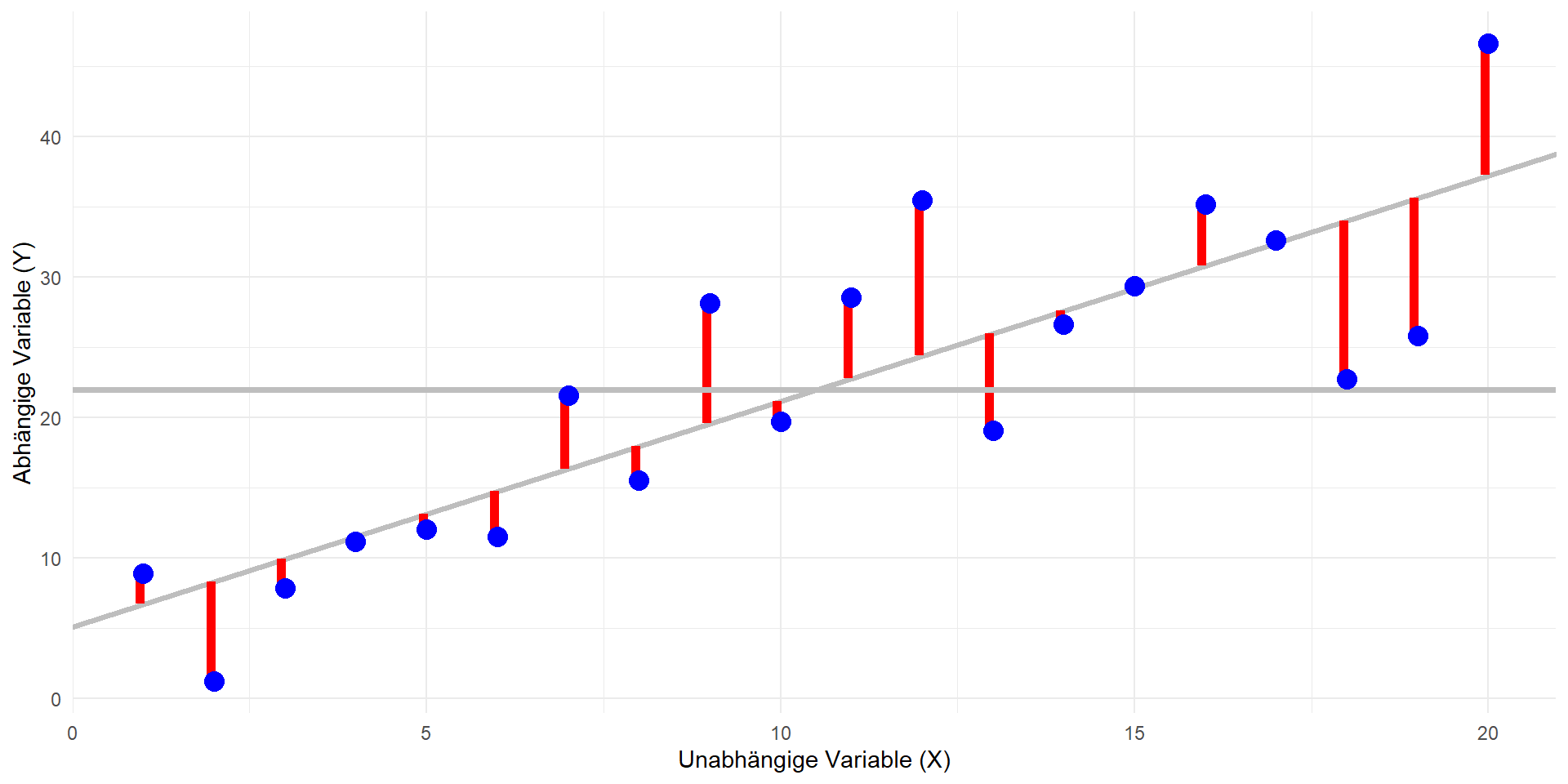
Quadratsummenzerlegung
\(QS_{tot} = QS_{mod} + QS_{res}\)
Formeln:
- \(QS_{tot} = \sum_{i}(y_i - \bar{y})^2\)
- \(QS_{res} = \sum_{i}(y_i - \hat{y_i})^2\)
- \(QS_{mod} = \sum_{i}(\hat{y_i} - \bar{y})^2\)
Hinweis: Bei allen Formeln wird über alle i summiert; d.h. jede Quadratsumme hat n Summanden.
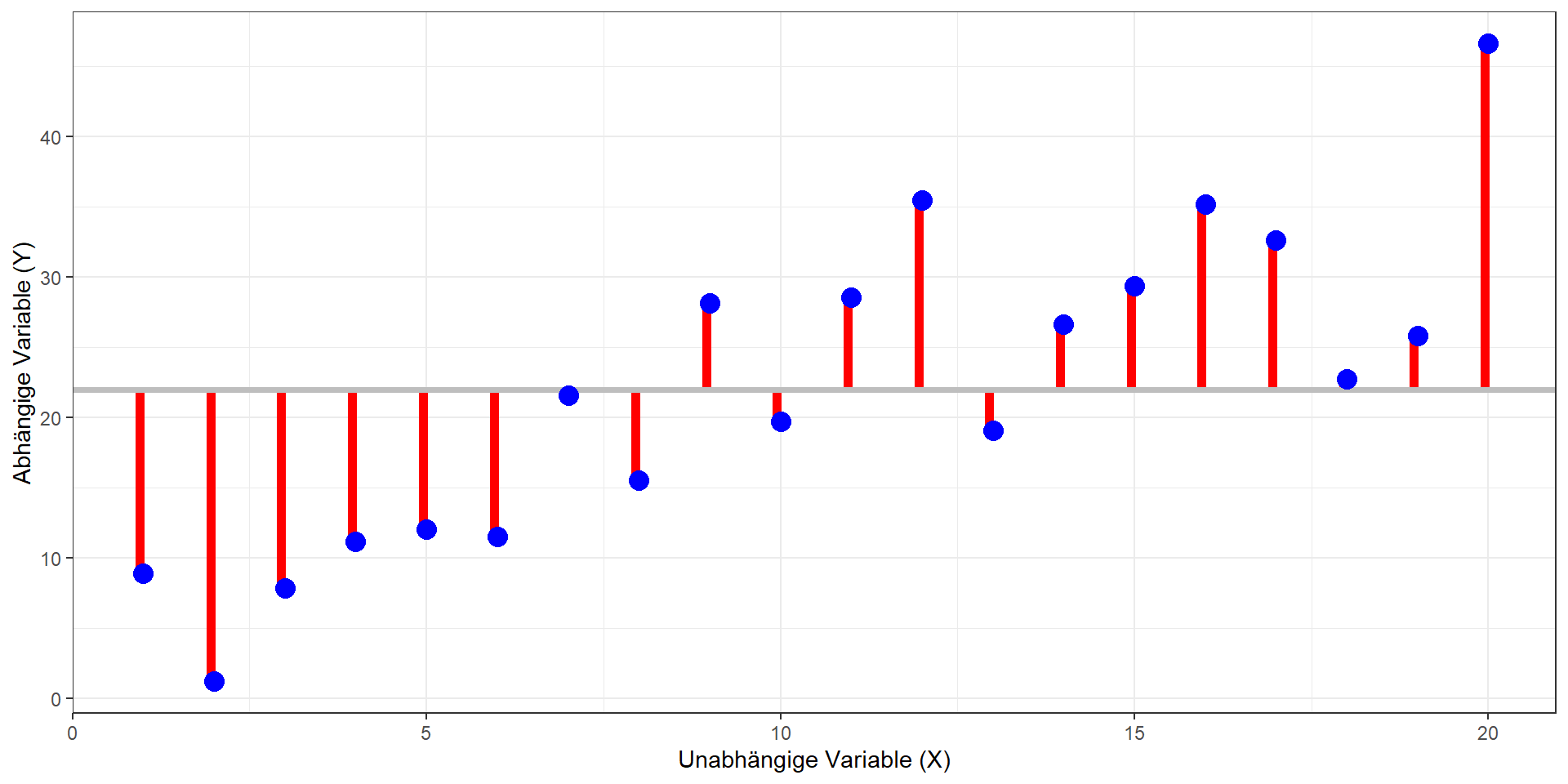
Modellgüte (einfach & multipel)
\(R^2\): Determinationskoeffizient, Bestimmtheitsmaß
Wie gut passt das Modell zu den Daten?
Maß der Varianzaufklärung (in Prozent) in der AV durch die UV
Berechnung: \(R^2 = QS_{mod}/QS_{tot}\)
Beispiele:
- \(R^2=0.6\): Varianzaufklärung = 60 %
- \(R^2=0.0\): Varianzaufklärung = 0 % (Unabhängigkeit)
- \(R^2=1.0\): Varianzaufklärung = 100 % (Determiniertheit)
Signifikanztest
Hypothesenpaar:
Einfache Regressionsanalyse
- \(H_0: b_1 = 0\) (also: keine Steigung der Regressionsgeraden; vgl. Nullmodell)
- \(H_1: b_1 ≠ 0\) (also: positive oder negative Steigung der Regressionsgeraden)
Multiple Regressionsanalyse
- \(H_0: b_1, b_2, ... b_n = 0\)
- \(H_1: b_j ≠ 0\) für mind. ein j = 1, 2, … n
Mittlere Quadratsummen & Freiheitsgrade:
- Freiheitsgrade des Modells: \(df_{mod}\) = Anzahl Prädiktoren
- Mittlere Modell-Quadratsumme: \(MQS_{mod} = QS_{mod}/df_{mod}\)
- Freiheitsgrade der Residuen: \(df_{res}\) = n - Anzahl Prädiktoren - 1
- Mittlere Residualquadratsumme: \(MQS_{res} = QS_{res}/df_{res}\)
Teststatistik:
- \(F = MQS_{mod}/MQS_{res}\)
- F-Verteilung (s. u.)
ANOVA-Tabelle
| Quelle | QS | df | MQS | F | p |
|---|---|---|---|---|---|
| Modell | QS\(_{mod}\) | df\(_{mod}\) | MQS\(_{mod}\) | F | p |
| Residuen | QS\(_{res}\) | df\(_{res}\) | MQS\(_{res}\) | ||
| Gesamt | QS\(_{tot}\) | df\(_{tot}\) | |||
Erläuterungen:
- QS\(_{tot}\) = QS\(_{mod}\) + QS\(_{res}\)
- df\(_{tot}\) = df\(_{mod}\) + df\(_{res}\)
- MQS\(_{mod}\) = QS\(_{mod}\)/df\(_{mod}\)
- MQS\(_{res}\) = QS\(_{res}\)/df\(_{res}\)
- F = MQS\(_{mod}\)/MQS\(_{res}\)
- p: p(F | H\(_0\))
F-Verteilung
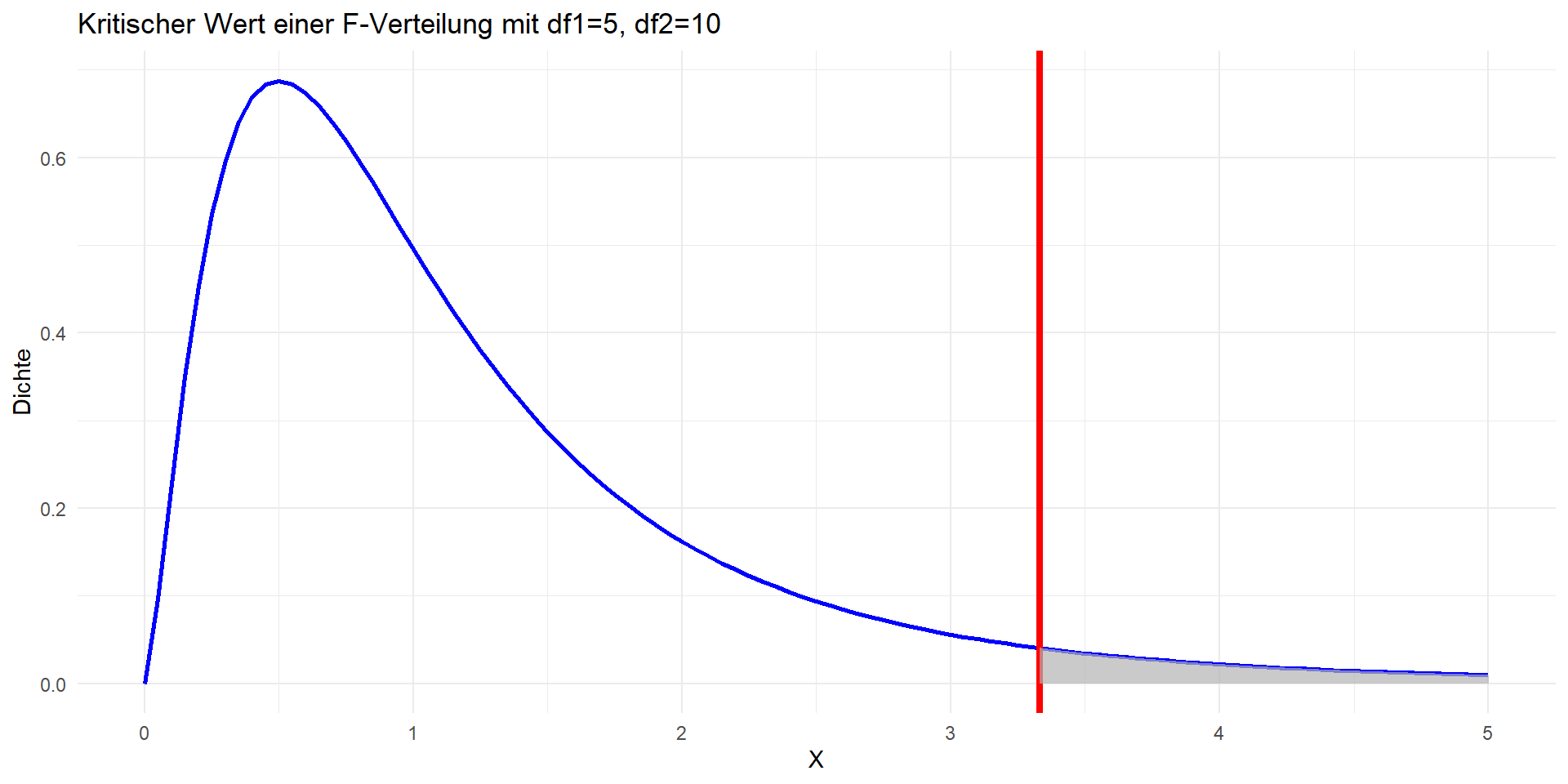
Kritische Werte der F-Verteilung
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 40 | 50 | 100 | Inf | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 161.45 | 199.50 | 215.71 | 224.58 | 230.16 | 233.99 | 236.77 | 238.88 | 240.54 | 241.88 | 242.98 | 243.91 | 244.69 | 245.36 | 245.95 | 246.46 | 246.92 | 247.32 | 247.69 | 248.01 | 248.31 | 248.58 | 248.83 | 249.05 | 249.26 | 249.45 | 249.63 | 249.80 | 249.95 | 250.10 | 251.14 | 251.77 | 253.04 | 254.31 |
| 2 | 18.51 | 19.00 | 19.16 | 19.25 | 19.30 | 19.33 | 19.35 | 19.37 | 19.38 | 19.40 | 19.40 | 19.41 | 19.42 | 19.42 | 19.43 | 19.43 | 19.44 | 19.44 | 19.44 | 19.45 | 19.45 | 19.45 | 19.45 | 19.45 | 19.46 | 19.46 | 19.46 | 19.46 | 19.46 | 19.46 | 19.47 | 19.48 | 19.49 | 19.50 |
| 3 | 10.13 | 9.55 | 9.28 | 9.12 | 9.01 | 8.94 | 8.89 | 8.85 | 8.81 | 8.79 | 8.76 | 8.74 | 8.73 | 8.71 | 8.70 | 8.69 | 8.68 | 8.67 | 8.67 | 8.66 | 8.65 | 8.65 | 8.64 | 8.64 | 8.63 | 8.63 | 8.63 | 8.62 | 8.62 | 8.62 | 8.59 | 8.58 | 8.55 | 8.53 |
| 4 | 7.71 | 6.94 | 6.59 | 6.39 | 6.26 | 6.16 | 6.09 | 6.04 | 6.00 | 5.96 | 5.94 | 5.91 | 5.89 | 5.87 | 5.86 | 5.84 | 5.83 | 5.82 | 5.81 | 5.80 | 5.79 | 5.79 | 5.78 | 5.77 | 5.77 | 5.76 | 5.76 | 5.75 | 5.75 | 5.75 | 5.72 | 5.70 | 5.66 | 5.63 |
| 5 | 6.61 | 5.79 | 5.41 | 5.19 | 5.05 | 4.95 | 4.88 | 4.82 | 4.77 | 4.74 | 4.70 | 4.68 | 4.66 | 4.64 | 4.62 | 4.60 | 4.59 | 4.58 | 4.57 | 4.56 | 4.55 | 4.54 | 4.53 | 4.53 | 4.52 | 4.52 | 4.51 | 4.50 | 4.50 | 4.50 | 4.46 | 4.44 | 4.41 | 4.36 |
| 6 | 5.99 | 5.14 | 4.76 | 4.53 | 4.39 | 4.28 | 4.21 | 4.15 | 4.10 | 4.06 | 4.03 | 4.00 | 3.98 | 3.96 | 3.94 | 3.92 | 3.91 | 3.90 | 3.88 | 3.87 | 3.86 | 3.86 | 3.85 | 3.84 | 3.83 | 3.83 | 3.82 | 3.82 | 3.81 | 3.81 | 3.77 | 3.75 | 3.71 | 3.67 |
| 7 | 5.59 | 4.74 | 4.35 | 4.12 | 3.97 | 3.87 | 3.79 | 3.73 | 3.68 | 3.64 | 3.60 | 3.57 | 3.55 | 3.53 | 3.51 | 3.49 | 3.48 | 3.47 | 3.46 | 3.44 | 3.43 | 3.43 | 3.42 | 3.41 | 3.40 | 3.40 | 3.39 | 3.39 | 3.38 | 3.38 | 3.34 | 3.32 | 3.27 | 3.23 |
| 8 | 5.32 | 4.46 | 4.07 | 3.84 | 3.69 | 3.58 | 3.50 | 3.44 | 3.39 | 3.35 | 3.31 | 3.28 | 3.26 | 3.24 | 3.22 | 3.20 | 3.19 | 3.17 | 3.16 | 3.15 | 3.14 | 3.13 | 3.12 | 3.12 | 3.11 | 3.10 | 3.10 | 3.09 | 3.08 | 3.08 | 3.04 | 3.02 | 2.97 | 2.93 |
| 9 | 5.12 | 4.26 | 3.86 | 3.63 | 3.48 | 3.37 | 3.29 | 3.23 | 3.18 | 3.14 | 3.10 | 3.07 | 3.05 | 3.03 | 3.01 | 2.99 | 2.97 | 2.96 | 2.95 | 2.94 | 2.93 | 2.92 | 2.91 | 2.90 | 2.89 | 2.89 | 2.88 | 2.87 | 2.87 | 2.86 | 2.83 | 2.80 | 2.76 | 2.71 |
| 10 | 4.96 | 4.10 | 3.71 | 3.48 | 3.33 | 3.22 | 3.14 | 3.07 | 3.02 | 2.98 | 2.94 | 2.91 | 2.89 | 2.86 | 2.85 | 2.83 | 2.81 | 2.80 | 2.79 | 2.77 | 2.76 | 2.75 | 2.75 | 2.74 | 2.73 | 2.72 | 2.72 | 2.71 | 2.70 | 2.70 | 2.66 | 2.64 | 2.59 | 2.54 |
| 11 | 4.84 | 3.98 | 3.59 | 3.36 | 3.20 | 3.09 | 3.01 | 2.95 | 2.90 | 2.85 | 2.82 | 2.79 | 2.76 | 2.74 | 2.72 | 2.70 | 2.69 | 2.67 | 2.66 | 2.65 | 2.64 | 2.63 | 2.62 | 2.61 | 2.60 | 2.59 | 2.59 | 2.58 | 2.58 | 2.57 | 2.53 | 2.51 | 2.46 | 2.40 |
| 12 | 4.75 | 3.89 | 3.49 | 3.26 | 3.11 | 3.00 | 2.91 | 2.85 | 2.80 | 2.75 | 2.72 | 2.69 | 2.66 | 2.64 | 2.62 | 2.60 | 2.58 | 2.57 | 2.56 | 2.54 | 2.53 | 2.52 | 2.51 | 2.51 | 2.50 | 2.49 | 2.48 | 2.48 | 2.47 | 2.47 | 2.43 | 2.40 | 2.35 | 2.30 |
| 13 | 4.67 | 3.81 | 3.41 | 3.18 | 3.03 | 2.92 | 2.83 | 2.77 | 2.71 | 2.67 | 2.63 | 2.60 | 2.58 | 2.55 | 2.53 | 2.51 | 2.50 | 2.48 | 2.47 | 2.46 | 2.45 | 2.44 | 2.43 | 2.42 | 2.41 | 2.41 | 2.40 | 2.39 | 2.39 | 2.38 | 2.34 | 2.31 | 2.26 | 2.21 |
| 14 | 4.60 | 3.74 | 3.34 | 3.11 | 2.96 | 2.85 | 2.76 | 2.70 | 2.65 | 2.60 | 2.57 | 2.53 | 2.51 | 2.48 | 2.46 | 2.44 | 2.43 | 2.41 | 2.40 | 2.39 | 2.38 | 2.37 | 2.36 | 2.35 | 2.34 | 2.33 | 2.33 | 2.32 | 2.31 | 2.31 | 2.27 | 2.24 | 2.19 | 2.13 |
| 15 | 4.54 | 3.68 | 3.29 | 3.06 | 2.90 | 2.79 | 2.71 | 2.64 | 2.59 | 2.54 | 2.51 | 2.48 | 2.45 | 2.42 | 2.40 | 2.38 | 2.37 | 2.35 | 2.34 | 2.33 | 2.32 | 2.31 | 2.30 | 2.29 | 2.28 | 2.27 | 2.27 | 2.26 | 2.25 | 2.25 | 2.20 | 2.18 | 2.12 | 2.07 |
| 16 | 4.49 | 3.63 | 3.24 | 3.01 | 2.85 | 2.74 | 2.66 | 2.59 | 2.54 | 2.49 | 2.46 | 2.42 | 2.40 | 2.37 | 2.35 | 2.33 | 2.32 | 2.30 | 2.29 | 2.28 | 2.26 | 2.25 | 2.24 | 2.24 | 2.23 | 2.22 | 2.21 | 2.21 | 2.20 | 2.19 | 2.15 | 2.12 | 2.07 | 2.01 |
| 17 | 4.45 | 3.59 | 3.20 | 2.96 | 2.81 | 2.70 | 2.61 | 2.55 | 2.49 | 2.45 | 2.41 | 2.38 | 2.35 | 2.33 | 2.31 | 2.29 | 2.27 | 2.26 | 2.24 | 2.23 | 2.22 | 2.21 | 2.20 | 2.19 | 2.18 | 2.17 | 2.17 | 2.16 | 2.15 | 2.15 | 2.10 | 2.08 | 2.02 | 1.96 |
| 18 | 4.41 | 3.55 | 3.16 | 2.93 | 2.77 | 2.66 | 2.58 | 2.51 | 2.46 | 2.41 | 2.37 | 2.34 | 2.31 | 2.29 | 2.27 | 2.25 | 2.23 | 2.22 | 2.20 | 2.19 | 2.18 | 2.17 | 2.16 | 2.15 | 2.14 | 2.13 | 2.13 | 2.12 | 2.11 | 2.11 | 2.06 | 2.04 | 1.98 | 1.92 |
| 19 | 4.38 | 3.52 | 3.13 | 2.90 | 2.74 | 2.63 | 2.54 | 2.48 | 2.42 | 2.38 | 2.34 | 2.31 | 2.28 | 2.26 | 2.23 | 2.21 | 2.20 | 2.18 | 2.17 | 2.16 | 2.14 | 2.13 | 2.12 | 2.11 | 2.11 | 2.10 | 2.09 | 2.08 | 2.08 | 2.07 | 2.03 | 2.00 | 1.94 | 1.88 |
| 20 | 4.35 | 3.49 | 3.10 | 2.87 | 2.71 | 2.60 | 2.51 | 2.45 | 2.39 | 2.35 | 2.31 | 2.28 | 2.25 | 2.22 | 2.20 | 2.18 | 2.17 | 2.15 | 2.14 | 2.12 | 2.11 | 2.10 | 2.09 | 2.08 | 2.07 | 2.07 | 2.06 | 2.05 | 2.05 | 2.04 | 1.99 | 1.97 | 1.91 | 1.84 |
| 21 | 4.32 | 3.47 | 3.07 | 2.84 | 2.68 | 2.57 | 2.49 | 2.42 | 2.37 | 2.32 | 2.28 | 2.25 | 2.22 | 2.20 | 2.18 | 2.16 | 2.14 | 2.12 | 2.11 | 2.10 | 2.08 | 2.07 | 2.06 | 2.05 | 2.05 | 2.04 | 2.03 | 2.02 | 2.02 | 2.01 | 1.96 | 1.94 | 1.88 | 1.81 |
| 22 | 4.30 | 3.44 | 3.05 | 2.82 | 2.66 | 2.55 | 2.46 | 2.40 | 2.34 | 2.30 | 2.26 | 2.23 | 2.20 | 2.17 | 2.15 | 2.13 | 2.11 | 2.10 | 2.08 | 2.07 | 2.06 | 2.05 | 2.04 | 2.03 | 2.02 | 2.01 | 2.00 | 2.00 | 1.99 | 1.98 | 1.94 | 1.91 | 1.85 | 1.78 |
| 23 | 4.28 | 3.42 | 3.03 | 2.80 | 2.64 | 2.53 | 2.44 | 2.37 | 2.32 | 2.27 | 2.24 | 2.20 | 2.18 | 2.15 | 2.13 | 2.11 | 2.09 | 2.08 | 2.06 | 2.05 | 2.04 | 2.02 | 2.01 | 2.01 | 2.00 | 1.99 | 1.98 | 1.97 | 1.97 | 1.96 | 1.91 | 1.88 | 1.82 | 1.76 |
| 24 | 4.26 | 3.40 | 3.01 | 2.78 | 2.62 | 2.51 | 2.42 | 2.36 | 2.30 | 2.25 | 2.22 | 2.18 | 2.15 | 2.13 | 2.11 | 2.09 | 2.07 | 2.05 | 2.04 | 2.03 | 2.01 | 2.00 | 1.99 | 1.98 | 1.97 | 1.97 | 1.96 | 1.95 | 1.95 | 1.94 | 1.89 | 1.86 | 1.80 | 1.73 |
| 25 | 4.24 | 3.39 | 2.99 | 2.76 | 2.60 | 2.49 | 2.40 | 2.34 | 2.28 | 2.24 | 2.20 | 2.16 | 2.14 | 2.11 | 2.09 | 2.07 | 2.05 | 2.04 | 2.02 | 2.01 | 2.00 | 1.98 | 1.97 | 1.96 | 1.96 | 1.95 | 1.94 | 1.93 | 1.93 | 1.92 | 1.87 | 1.84 | 1.78 | 1.71 |
| 26 | 4.23 | 3.37 | 2.98 | 2.74 | 2.59 | 2.47 | 2.39 | 2.32 | 2.27 | 2.22 | 2.18 | 2.15 | 2.12 | 2.09 | 2.07 | 2.05 | 2.03 | 2.02 | 2.00 | 1.99 | 1.98 | 1.97 | 1.96 | 1.95 | 1.94 | 1.93 | 1.92 | 1.91 | 1.91 | 1.90 | 1.85 | 1.82 | 1.76 | 1.69 |
| 27 | 4.21 | 3.35 | 2.96 | 2.73 | 2.57 | 2.46 | 2.37 | 2.31 | 2.25 | 2.20 | 2.17 | 2.13 | 2.10 | 2.08 | 2.06 | 2.04 | 2.02 | 2.00 | 1.99 | 1.97 | 1.96 | 1.95 | 1.94 | 1.93 | 1.92 | 1.91 | 1.90 | 1.90 | 1.89 | 1.88 | 1.84 | 1.81 | 1.74 | 1.67 |
| 28 | 4.20 | 3.34 | 2.95 | 2.71 | 2.56 | 2.45 | 2.36 | 2.29 | 2.24 | 2.19 | 2.15 | 2.12 | 2.09 | 2.06 | 2.04 | 2.02 | 2.00 | 1.99 | 1.97 | 1.96 | 1.95 | 1.93 | 1.92 | 1.91 | 1.91 | 1.90 | 1.89 | 1.88 | 1.88 | 1.87 | 1.82 | 1.79 | 1.73 | 1.65 |
| 29 | 4.18 | 3.33 | 2.93 | 2.70 | 2.55 | 2.43 | 2.35 | 2.28 | 2.22 | 2.18 | 2.14 | 2.10 | 2.08 | 2.05 | 2.03 | 2.01 | 1.99 | 1.97 | 1.96 | 1.94 | 1.93 | 1.92 | 1.91 | 1.90 | 1.89 | 1.88 | 1.88 | 1.87 | 1.86 | 1.85 | 1.81 | 1.77 | 1.71 | 1.64 |
| 30 | 4.17 | 3.32 | 2.92 | 2.69 | 2.53 | 2.42 | 2.33 | 2.27 | 2.21 | 2.16 | 2.13 | 2.09 | 2.06 | 2.04 | 2.01 | 1.99 | 1.98 | 1.96 | 1.95 | 1.93 | 1.92 | 1.91 | 1.90 | 1.89 | 1.88 | 1.87 | 1.86 | 1.85 | 1.85 | 1.84 | 1.79 | 1.76 | 1.70 | 1.62 |
| 40 | 4.08 | 3.23 | 2.84 | 2.61 | 2.45 | 2.34 | 2.25 | 2.18 | 2.12 | 2.08 | 2.04 | 2.00 | 1.97 | 1.95 | 1.92 | 1.90 | 1.89 | 1.87 | 1.85 | 1.84 | 1.83 | 1.81 | 1.80 | 1.79 | 1.78 | 1.77 | 1.77 | 1.76 | 1.75 | 1.74 | 1.69 | 1.66 | 1.59 | 1.51 |
| 50 | 4.03 | 3.18 | 2.79 | 2.56 | 2.40 | 2.29 | 2.20 | 2.13 | 2.07 | 2.03 | 1.99 | 1.95 | 1.92 | 1.89 | 1.87 | 1.85 | 1.83 | 1.81 | 1.80 | 1.78 | 1.77 | 1.76 | 1.75 | 1.74 | 1.73 | 1.72 | 1.71 | 1.70 | 1.69 | 1.69 | 1.63 | 1.60 | 1.52 | 1.44 |
| 100 | 3.94 | 3.09 | 2.70 | 2.46 | 2.31 | 2.19 | 2.10 | 2.03 | 1.97 | 1.93 | 1.89 | 1.85 | 1.82 | 1.79 | 1.77 | 1.75 | 1.73 | 1.71 | 1.69 | 1.68 | 1.66 | 1.65 | 1.64 | 1.63 | 1.62 | 1.61 | 1.60 | 1.59 | 1.58 | 1.57 | 1.52 | 1.48 | 1.39 | 1.28 |
| Inf | 3.84 | 3.00 | 2.60 | 2.37 | 2.21 | 2.10 | 2.01 | 1.94 | 1.88 | 1.83 | 1.79 | 1.75 | 1.72 | 1.69 | 1.67 | 1.64 | 1.62 | 1.60 | 1.59 | 1.57 | 1.56 | 1.54 | 1.53 | 1.52 | 1.51 | 1.50 | 1.49 | 1.48 | 1.47 | 1.46 | 1.39 | 1.35 | 1.24 | 1.00 |
Voraussetzungen, Stichprobenumfang & Effektstärke
Voraussetzungen
- Gültigkeit des linearen Modells
- Kriterium mind. intervallskaliert
- Prädiktor nominal-, intervall- oder verhältnisskaliert (nominal: Dummy-Codierung mit 0 und 1)
- Normalverteilung der Residuen
- Statistische Unabhängigkeit der Residuen voneinander (keine Autokorrelation)
- Homoskedastizität (Varianz der Residuen ist unabhängig vom X-Wert. Die Streuung nimmt nicht mit der Größe der X-Werte zu)
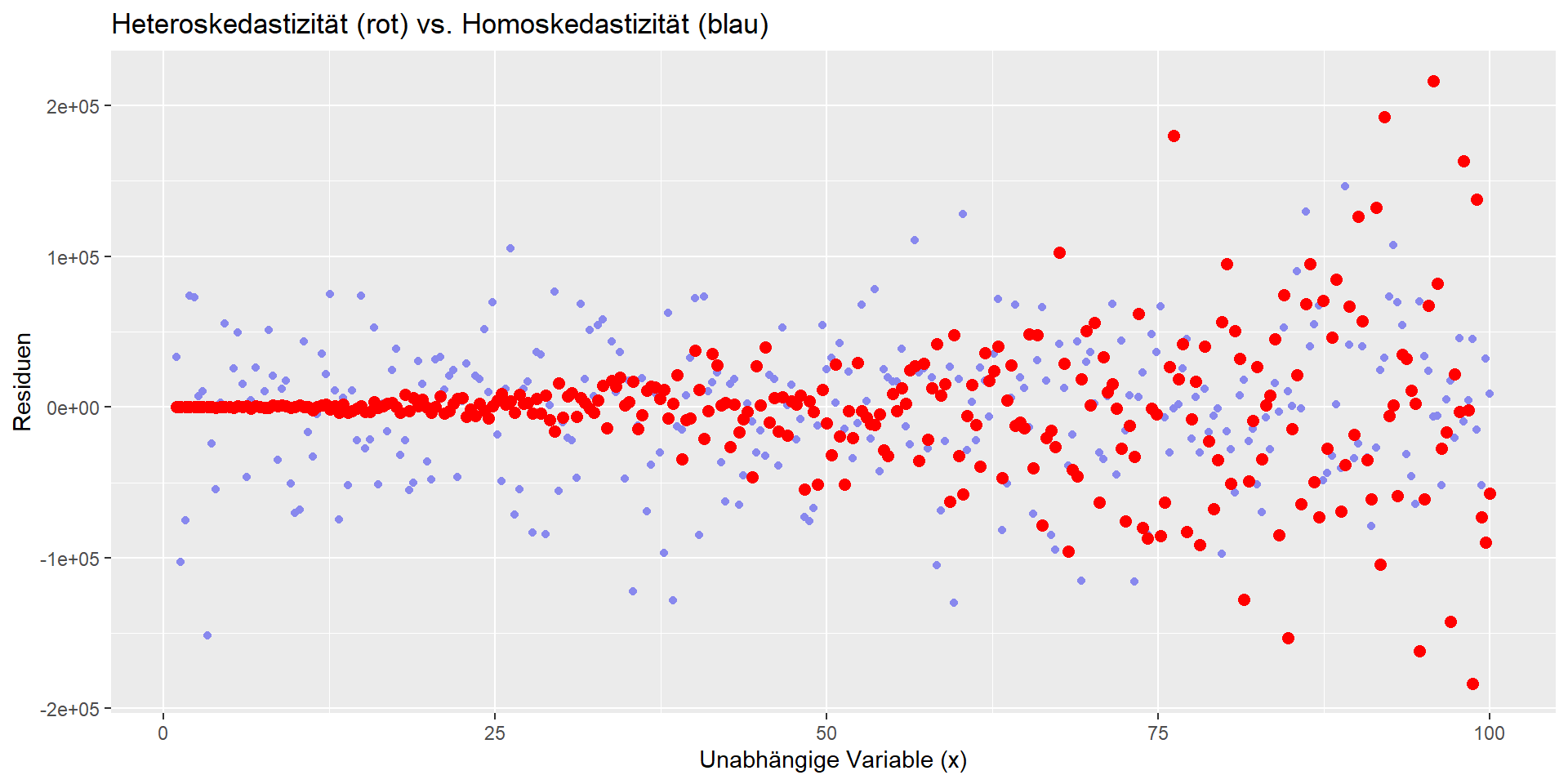
Homoskedastizität vs. Heteroskedastizität
- Homoskedastizität: Varianz der Residuen ist unabhängig vom X-Wert. Die Streuung nimmt nicht mit der Größe der X-Werte zu.
- Visuelles Kennzeichen: Strukturlose Punktewolke (i.G.z. Trichter-Form bei Heteroskedastizität)
Planung der Stichprobengröße
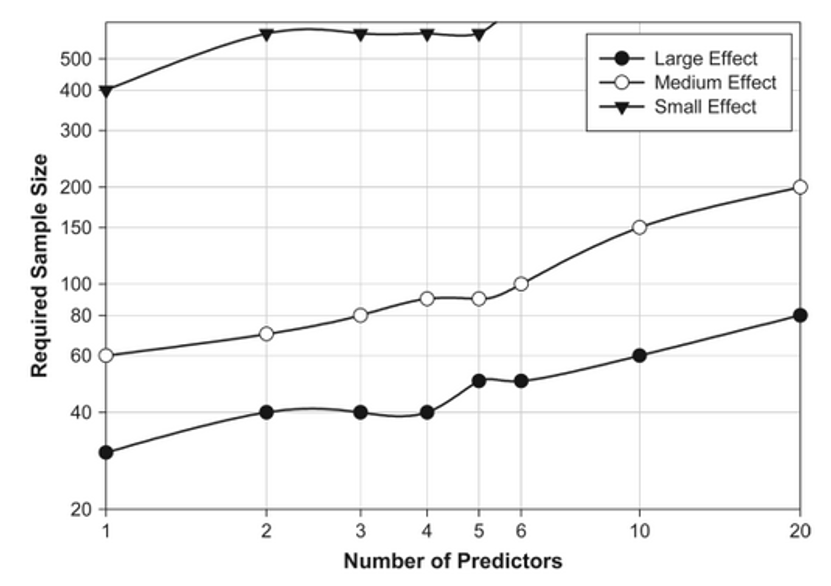
Beispiel PKW
| PKW.Name | Tueren | Plaetze | Laenge | Gewicht | Hubraum | Leistung | Vmax | Beschl. | Airbags | Verbrauch | Preis |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mercedes CL 500 | 2 | 5 | 499 | 1865 | 4966 | 225 | 250 | 6.5 | 4 | 12.5 | 155667 |
| Mercedes CLK 200 | 2 | 5 | 457 | 1375 | 1998 | 100 | 208 | 11.0 | 2 | 9.4 | 54673 |
| Mercedes E 200 | 4 | 5 | 480 | 1510 | 1998 | 100 | 209 | 9.3 | 6 | 9.3 | 53453 |
| Mercedes S 320 | 4 | 5 | 504 | 1770 | 3199 | 165 | 240 | 8.2 | 6 | 11.5 | 110664 |
| Mercedes SL 280 | 2 | 2 | 447 | 1810 | 2799 | 150 | 232 | 9.7 | 2 | 11.4 | 117206 |
| Mercedes SLK 200 | 2 | 2 | 401 | 1364 | 1998 | 120 | 223 | 8.2 | 4 | 9.6 | 50863 |
| Merzedes A 140 | 5 | 5 | 358 | 1095 | 1397 | 60 | 170 | 12.9 | 2 | 7.1 | 25414 |
Kann mit Hilfe der Leistung der Verbrauch vorhergesagt (= linear modelliert) werden?
Lineares Modell:
Verbrauch = 5.872 + 0.032\(\cdot\)Leistung
Determinationskoeffizient: 0.918
Teststatistik: F(1, 5) = 56.132
Kritischer F-Wert: 6.608
p-Wert: 0.0007
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.87152806 0.605748186 9.693018 0.0001984797
Leistung 0.03228185 0.004308753 7.492157 0.0006695017Analysis of Variance Table
Response: Verbrauch
Df Sum Sq Mean Sq F value Pr(>F)
Leistung 1 18.1701 18.1701 56.132 0.0006695 ***
Residuals 5 1.6185 0.3237
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1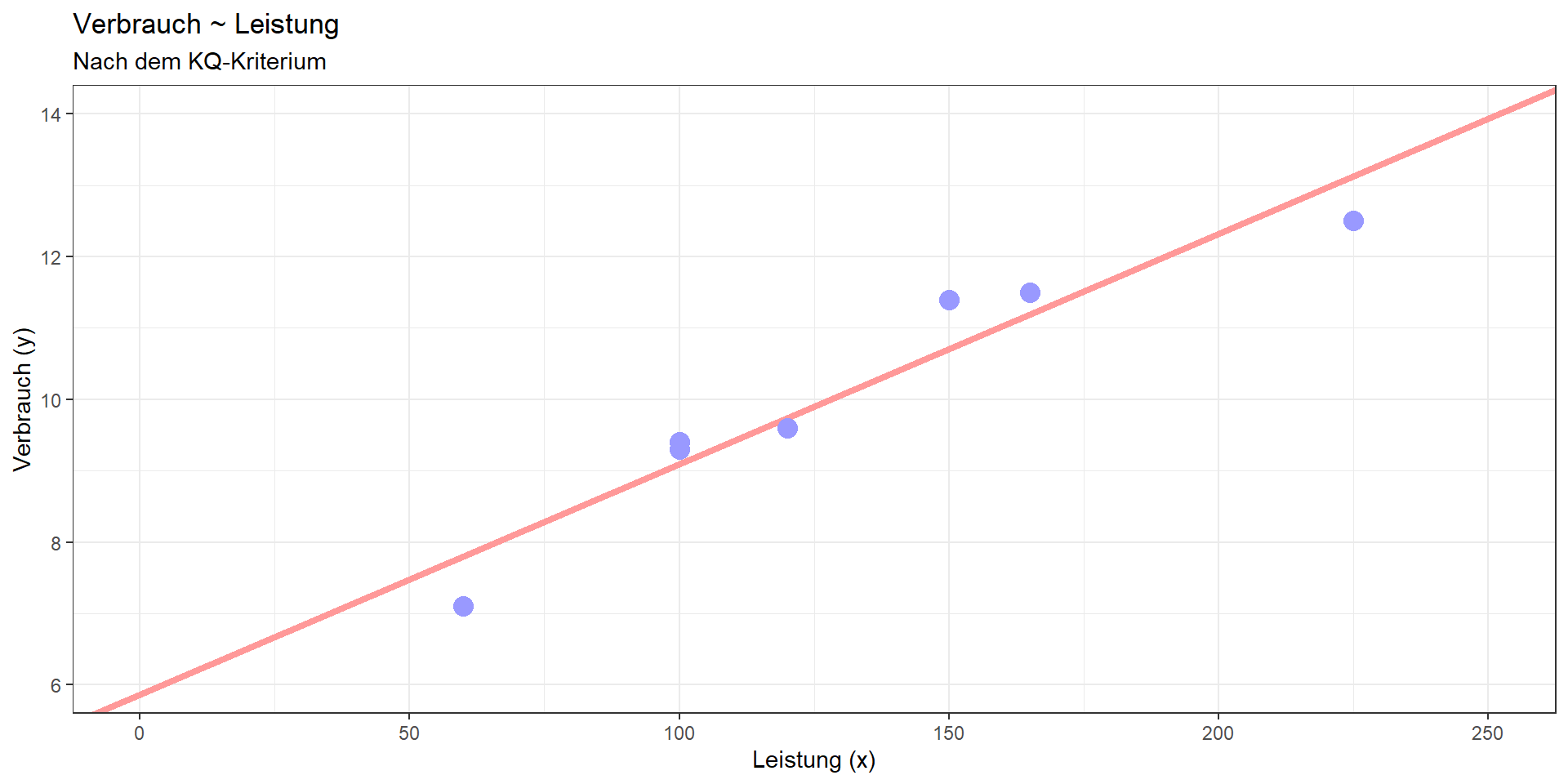
Beispiel PKW (2)
| PKW.Name | Leistung | Verbrauch | Modellvorhersage | QS_tot_values | QS_mod_values | QS_res_values |
|---|---|---|---|---|---|---|
| Mercedes CL 500 | 225 | 12.5 | 13.135 | 5.692 | 9.124 | 0.403 |
| Mercedes CLK 200 | 100 | 9.4 | 9.100 | 0.510 | 1.029 | 0.090 |
| Mercedes E 200 | 100 | 9.3 | 9.100 | 0.663 | 1.029 | 0.040 |
| Mercedes S 320 | 165 | 11.5 | 11.198 | 1.920 | 1.175 | 0.091 |
| Mercedes SL 280 | 150 | 11.4 | 10.714 | 1.653 | 0.359 | 0.471 |
| Mercedes SLK 200 | 120 | 9.6 | 9.745 | 0.264 | 0.136 | 0.021 |
| Merzedes A 140 | 60 | 7.1 | 7.808 | 9.086 | 5.317 | 0.502 |
Verbrauch = 5.872 + 0.032\(\cdot\)Leistung
Quadratsummen (QS\(_{tot}\) = QS\(_{mod}\) + QS\(_{res}\)):
- QS\(_{tot}\) = 19.788
- QS\(_{mod}\) = 18.169
- QS\(_{res}\) = 1.618
Mittlere Quadratsummen:
- MQS\(_{mod}\) = 18.169
- MQS\(_{res}\) = 0.3236
F(1, 5) = MQS\(_{mod}\)/MQS\(_{res}\) = 18.169/0.324 = 56.146
R² = QS\(_{mod}\)/QS\(_{tot}\) = 18.169/19.788 = 0.918
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.87152806 0.605748186 9.693018 0.0001984797
Leistung 0.03228185 0.004308753 7.492157 0.0006695017Analysis of Variance Table
Response: Verbrauch
Df Sum Sq Mean Sq F value Pr(>F)
Leistung 1 18.1701 18.1701 56.132 0.0006695 ***
Residuals 5 1.6185 0.3237
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1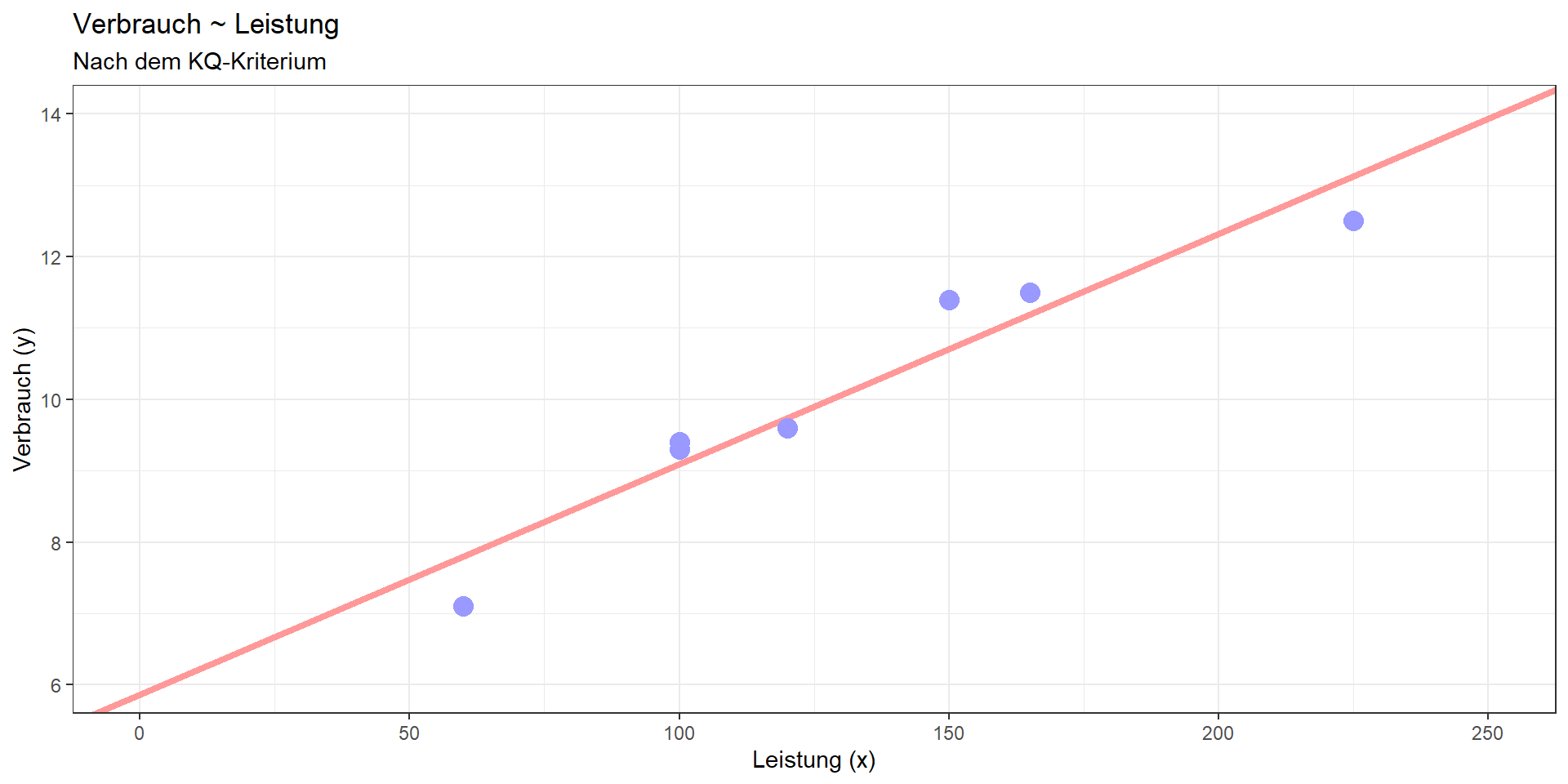
Effektstärke
Formel: \(f^2 = \frac{R^2}{1-R^2}\)
Interpretation für einen Prädiktor:
- f² = 0.01 \(\rightarrow\) kleiner Effekt
- f² = 0.10 \(\rightarrow\) mittlerer Effekt
- f² = 0.33 \(\rightarrow\) starker Effekt
Interpretation für mehrere Prädiktoren:
- f² = 0.02 \(\rightarrow\) kleiner Effekt
- f² = 0.15 \(\rightarrow\) mittlerer Effekt
- f² = 0.35 \(\rightarrow\) starker Effekt
Multiple lineare Regressionsanalyse
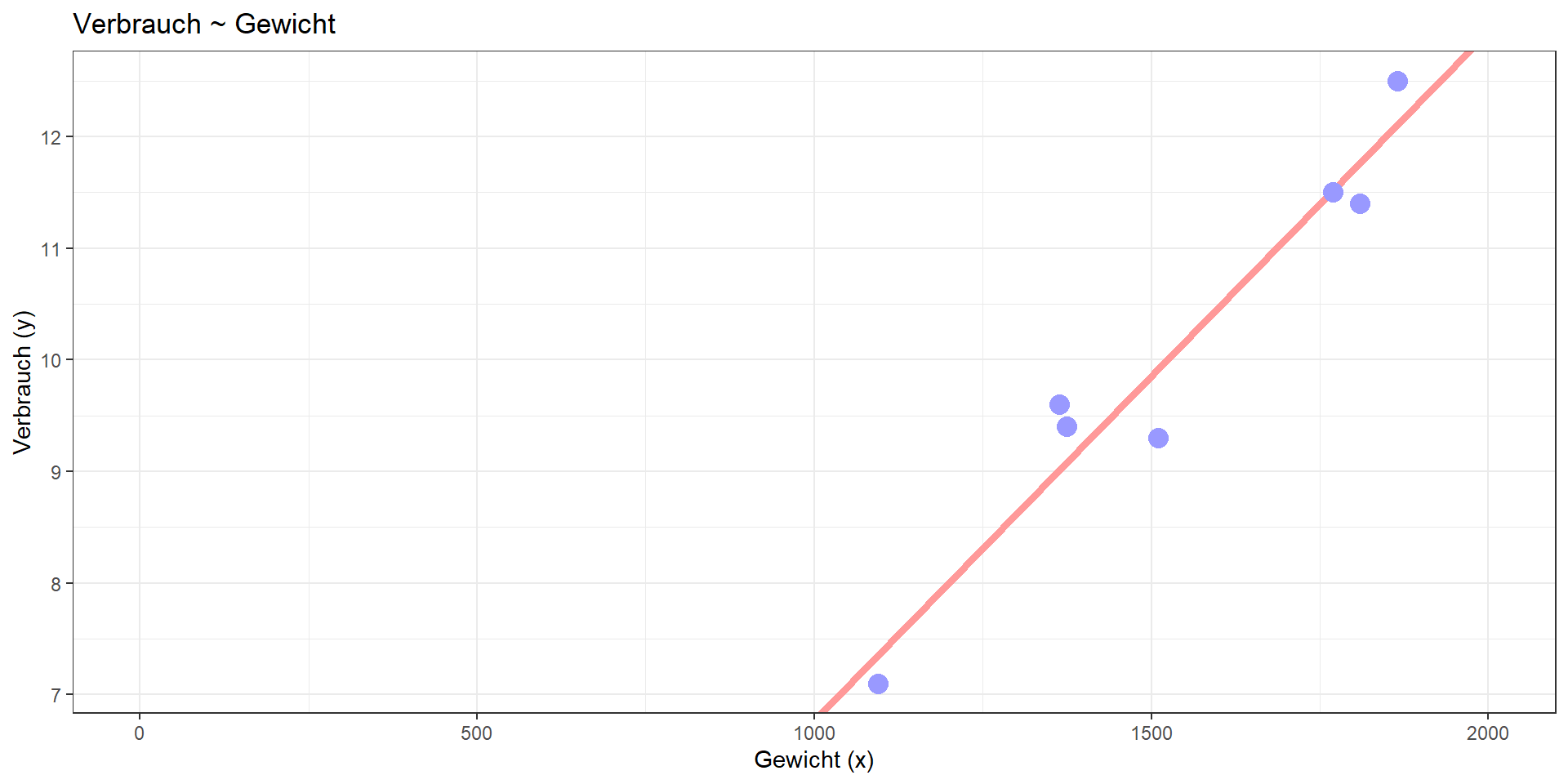
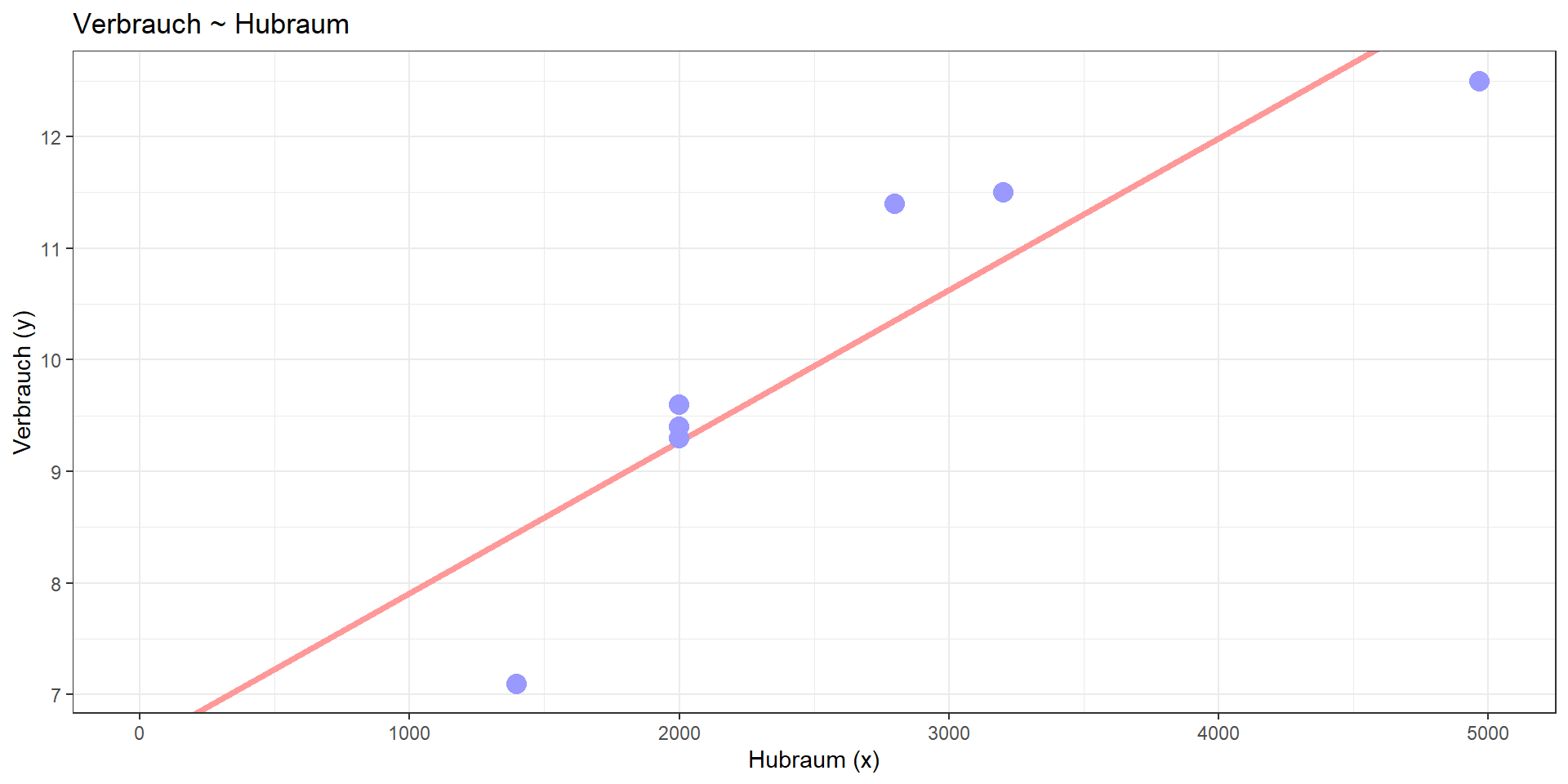
Beispiel PKW (multipel)
| PKW.Name | Leistung | Gewicht | Hubraum | Verbrauch | Modellvorhersage | Residuen | QS_tot_values | QS_mod_values | QS_res_values |
|---|---|---|---|---|---|---|---|---|---|
| Mercedes CL 500 | 225 | 1865 | 4966 | 12.5 | 12.515 | -0.015 | 5.692 | 5.762 | 0.000 |
| Mercedes CLK 200 | 100 | 1375 | 1998 | 9.4 | 9.009 | 0.391 | 0.510 | 1.222 | 0.153 |
| Mercedes E 200 | 100 | 1510 | 1998 | 9.3 | 9.413 | -0.113 | 0.663 | 0.492 | 0.013 |
| Mercedes S 320 | 165 | 1770 | 3199 | 11.5 | 11.518 | -0.018 | 1.920 | 1.971 | 0.000 |
| Mercedes SL 280 | 150 | 1810 | 2799 | 11.4 | 11.428 | -0.028 | 1.653 | 1.725 | 0.001 |
| Mercedes SLK 200 | 120 | 1364 | 1998 | 9.6 | 9.672 | -0.072 | 0.264 | 0.196 | 0.005 |
| Merzedes A 140 | 60 | 1095 | 1397 | 7.1 | 7.246 | -0.146 | 9.086 | 8.226 | 0.021 |
Kann mit Hilfe von Leistung, Gewicht und Hubraum der Verbrauch besser vorhergesagt (= linear modelliert) werden?
Lineares Modell:
Verbrauch = 2.967 + 0.035\(\cdot\)Leistung + 0.003\(\cdot\)Gewicht -0.001\(\cdot\)Hubraum
Determinationskoeffizient: R² = 0.99
Multipler Korrelationskoeffizient: R = 0.995
Teststatistik: F(3, 3) = 101.148
Kritischer F-Wert: 9.277
p-Wert: 0.00164
Effektstärke: f² = 99 (ein extrem starker Effekt!)
Quadratsummen (QS\(_{tot}\) = QS\(_{mod}\) + QS\(_{res}\)):
- QS\(_{tot}\) = 19.788
- QS\(_{mod}\) = 19.594
- QS\(_{res}\) = 0.193
ANOVA-Tabelle
| Quelle | QS | df | MQS | F | p |
|---|---|---|---|---|---|
| Modell | 19.594 | 3 | 6.531 | 101.148 | 0.00164 |
| Residuen | 0.193 | 3 | 0.064 | ||
| Gesamt | 19.788 | 6 | |||
Beispiel PKW (multipel) – Details
Call:
lm(formula = Verbrauch ~ Leistung + Gewicht + Hubraum)
Residuals:
1 2 3 4 5 6 7
-0.01473 0.39137 -0.11294 -0.01830 -0.02760 -0.07167 -0.14612
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.9666585 0.8363001 3.547 0.0382 *
Leistung 0.0347992 0.0114315 3.044 0.0557 .
Gewicht 0.0029949 0.0008949 3.347 0.0442 *
Hubraum -0.0007787 0.0004177 -1.864 0.1591
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2541 on 3 degrees of freedom
Multiple R-squared: 0.9902, Adjusted R-squared: 0.9804
F-statistic: 101.1 on 3 and 3 DF, p-value: 0.00164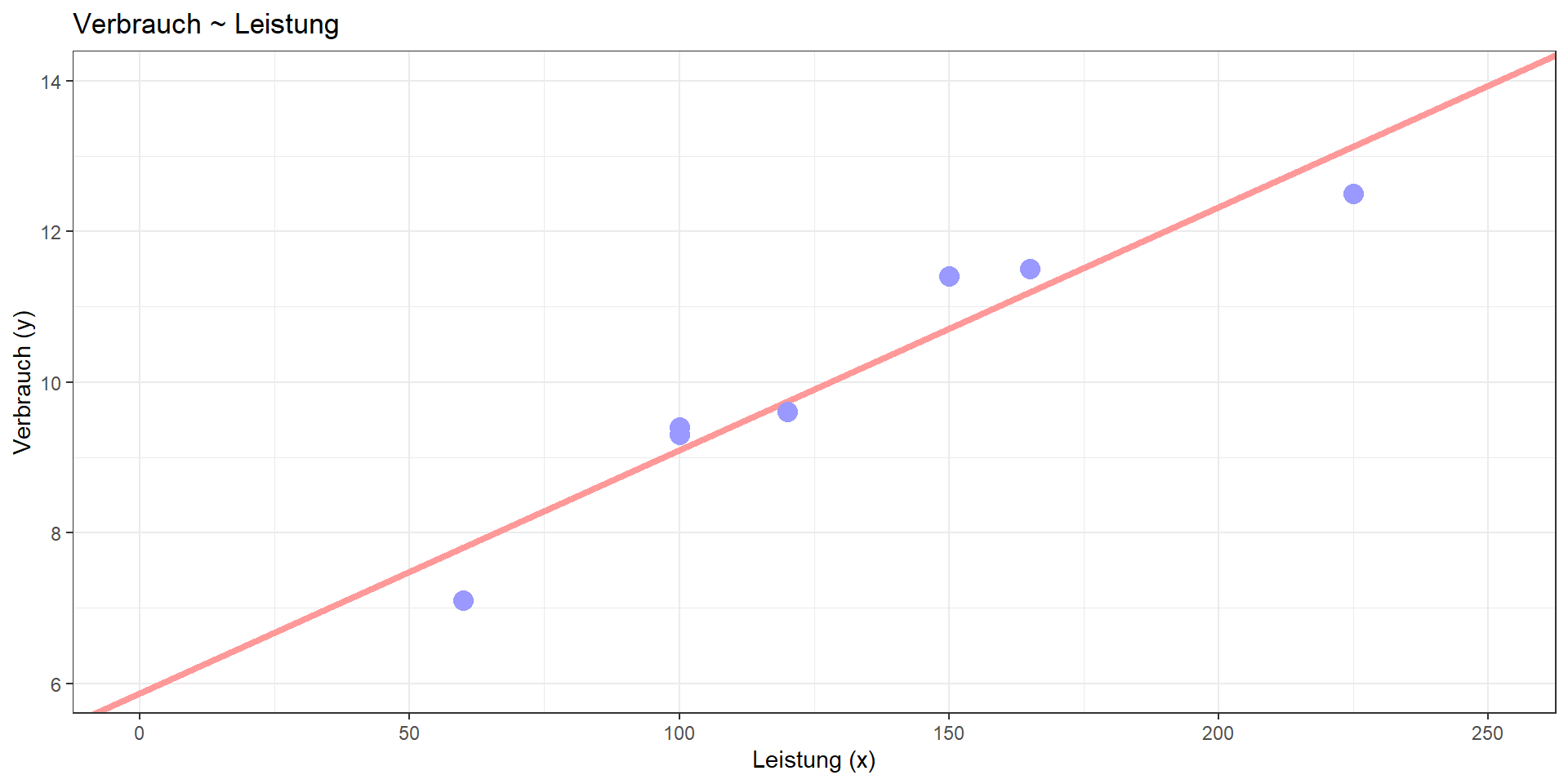
Modell(notationen)
- Modell mit un-standardisierten \(b\)-Koeffizienten:
\(y = b_0 + b_1x_1 + b_2x_2 + \dots +\,b_nx_n + \epsilon\) - Modell mit standardisierten \(\beta\)-Koeffizienten:
\(y = \beta_1x_1 + \beta_2x_2 + \dots +\,\beta_nx_n + \epsilon\)- Ausgangspunkt: z-standardisierte Variablen (Kriterium + Prädiktoren)
- Hauptunterschied: Modell (Gerade, Fläche, … ) geht durch den Ursprung (kein \(\beta_0\)!)
- Interpretation der Koeffizienten:
- \(b_i\): Steigt Prädiktor \(i\) um eine Einheit, steigt das Kriterium um \(b_i\) Einheiten
- \(\beta_i\): Steigt Prädiktor \(i\) um eine Standardabweichung, steigt das Kriterium um \(\beta_i\) Standardabweichungen
- Vorteil der \(\beta\)-Notation: Alle Prädiktoren haben dieselbe Einheit (= Standardabweichung) und können damit in ihrer Bedeutung verglichen werden
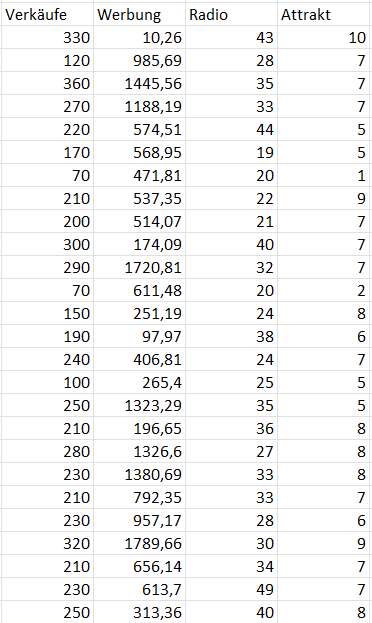
♪♫ Beispiel: Albumverkäufe
- Chef einer Musikfirma möchte seine Verkaufszahlen vorhersagen
- Daten zu 200 verschiedenen Alben (n = 200)
- Kriterium (AV): Albumverkäufe in der Woche nach Veröffentlichung (in 1.000 Stück)
- Prädiktor 1 (UV1): Werbebudget (in 1.000 Pfund)
- Prädiktor 2 (UV2): Radiohäufigkeit (in 1.000 mal pro Woche)
- Prädiktor 3 (UV3): Attraktivität (1 bis 10)
- Modell: Albumverkäufe = \(b_0\) + \(b_1\) Werbebudget + \(b_2\) Radiohäufigkeit
+ \(b_3\) Attraktivität + Fehler
♪♫ Modell mit einem Prädiktor
Call:
lm(formula = Verkäufe ~ Werbung)
Residuals:
Min 1Q Median 3Q Max
-152.949 -43.796 -0.393 37.040 211.866
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.341e+02 7.537e+00 17.799 <2e-16 ***
Werbung 9.612e-02 9.632e-03 9.979 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 65.99 on 198 degrees of freedom
Multiple R-squared: 0.3346, Adjusted R-squared: 0.3313
F-statistic: 99.59 on 1 and 198 DF, p-value: < 2.2e-16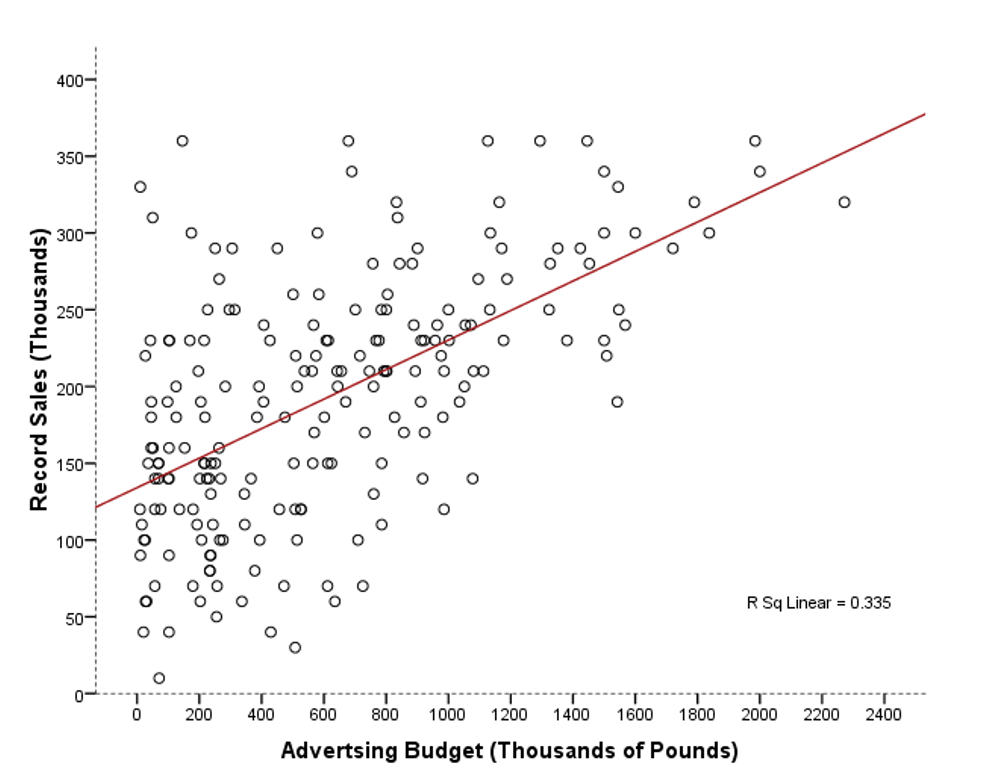
♪♫ Modell mit zwei Prädiktoren
Hinweis: Die Funktion lm() nimmt mehrere Prädiktoren gleichzeitig in das Modell auf (i. Ggs. z. hierarchischem Ansatz). Die Funktion lm.beta() liefert die standardisierten Beta-Werte.
Call:
lm(formula = Verkäufe ~ Werbung + Radiohäufigkeit)
Residuals:
Min 1Q Median 3Q Max
-112.121 -30.027 3.952 32.072 155.498
Coefficients:
Estimate Standardized Std. Error t value Pr(>|t|)
(Intercept) 41.123811 NA 9.330952 4.407 1.72e-05 ***
Werbung 0.086887 0.522896 0.007246 11.991 < 2e-16 ***
Radiohäufigkeit 3.588789 0.545645 0.286807 12.513 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 49.38 on 197 degrees of freedom
Multiple R-squared: 0.6293, Adjusted R-squared: 0.6255
F-statistic: 167.2 on 2 and 197 DF, p-value: < 2.2e-16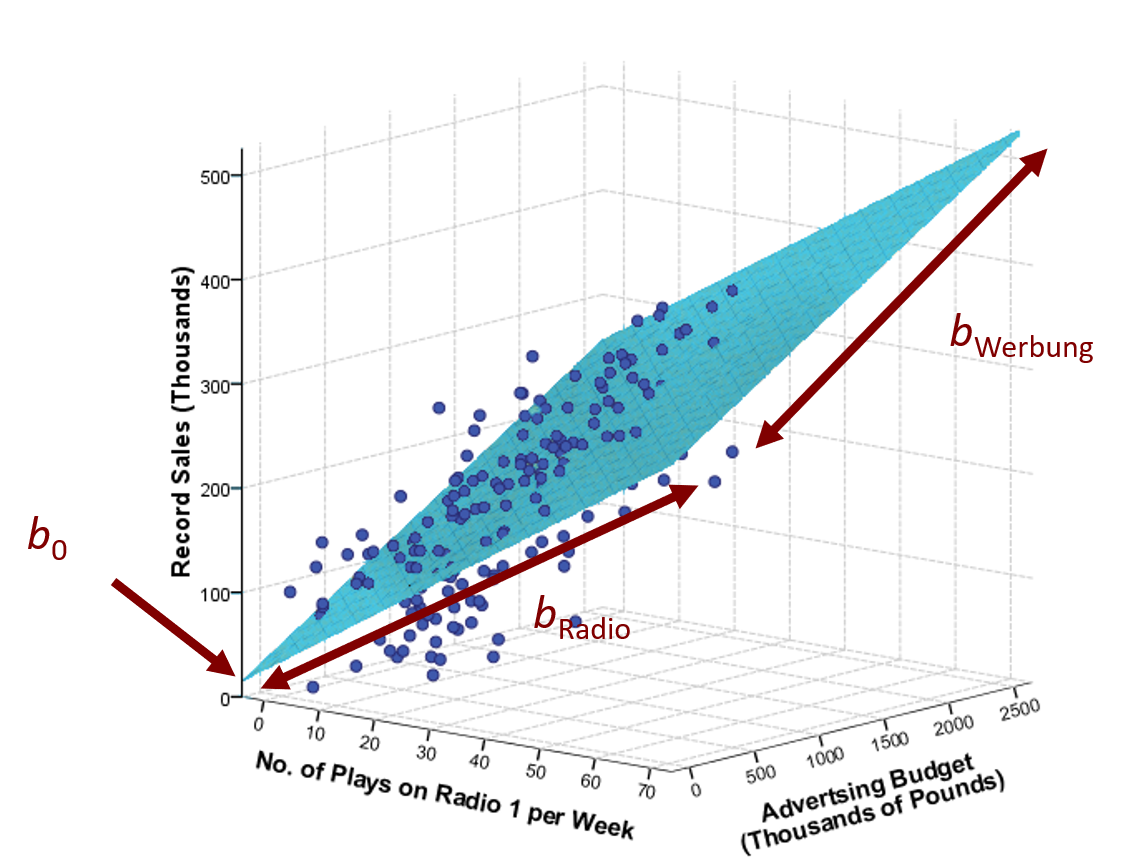
♪♫ Modell mit drei Prädiktoren
Call:
lm(formula = Verkäufe ~ Werbung + Radiohäufigkeit + Attraktivität)
Residuals:
Min 1Q Median 3Q Max
-121.324 -28.336 -0.451 28.967 144.132
Coefficients:
Estimate Standardized Std. Error t value Pr(>|t|)
(Intercept) -26.612958 NA 17.350001 -1.534 0.127
Werbung 0.084885 0.510846 0.006923 12.261 < 2e-16 ***
Radiohäufigkeit 3.367425 0.511988 0.277771 12.123 < 2e-16 ***
Attraktivität 11.086335 0.191683 2.437849 4.548 9.49e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 47.09 on 196 degrees of freedom
Multiple R-squared: 0.6647, Adjusted R-squared: 0.6595
F-statistic: 129.5 on 3 and 196 DF, p-value: < 2.2e-16♪♫ ANOVA-Tabellen
Achtung: Hier wird ein hierarchischer Ansatz gewählt. Das bedeutet, dass die Prädiktoren in einer bestimmten Reihenfolge in das Modell aufgenommen werden, was für die Analyse wichtig ist (i. Ggs. z. lm(...); die Reihenfolge stammt aus der Modellbeschreibung in lm()). Die Tabellen liefert die Funktion anova().
Ein Prädiktor
Analysis of Variance Table
Response: Verkäufe
Df Sum Sq Mean Sq F value Pr(>F)
Werbung 1 433688 433688 99.587 < 2.2e-16 ***
Residuals 198 862264 4355
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Zwei Prädiktoren
Analysis of Variance Table
Response: Verkäufe
Df Sum Sq Mean Sq F value Pr(>F)
Werbung 1 433688 433688 177.83 < 2.2e-16 ***
Radiohäufigkeit 1 381836 381836 156.57 < 2.2e-16 ***
Residuals 197 480428 2439
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Drei Prädiktoren
Analysis of Variance Table
Response: Verkäufe
Df Sum Sq Mean Sq F value Pr(>F)
Werbung 1 433688 433688 195.600 < 2.2e-16 ***
Radiohäufigkeit 1 381836 381836 172.214 < 2.2e-16 ***
Attraktivität 1 45853 45853 20.681 9.492e-06 ***
Residuals 196 434575 2217
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1♪♫ Zwei oder drei UVs?
Analysis of Variance Table
Model 1: Verkäufe ~ Werbung + Radiohäufigkeit
Model 2: Verkäufe ~ Werbung + Radiohäufigkeit + Attraktivität
Res.Df RSS Df Sum of Sq F Pr(>F)
1 197 480428
2 196 434575 1 45853 20.681 9.492e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Die an den Freiheitsgraden (1) relativierte Differenz der Quadratsummen (45853) wird an der mittleren Residualquadratsumme des zweiten Modells (434575/196) getestet:
F = \(\frac{45853/1}{434575/196}\) = 20.681Es gibt also einen signifikanten Unterschied zwischen den beiden Modellen:
F(1, 196) = 20.681; p < .001Das zweite Modell ist signifikant besser!
♪♫ Interpretation von Modell 3
Call:
lm(formula = Verkäufe ~ Werbung + Radiohäufigkeit + Attraktivität)
Residuals:
Min 1Q Median 3Q Max
-121.324 -28.336 -0.451 28.967 144.132
Coefficients:
Estimate Standardized Std. Error t value Pr(>|t|)
(Intercept) -26.612958 NA 17.350001 -1.534 0.127
Werbung 0.084885 0.510846 0.006923 12.261 < 2e-16 ***
Radiohäufigkeit 3.367425 0.511988 0.277771 12.123 < 2e-16 ***
Attraktivität 11.086335 0.191683 2.437849 4.548 9.49e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 47.09 on 196 degrees of freedom
Multiple R-squared: 0.6647, Adjusted R-squared: 0.6595
F-statistic: 129.5 on 3 and 196 DF, p-value: < 2.2e-16Modell:
Verkäufe = -26.613 + 0.085 Werbung + 3.367 Radiohäufigkeit +
11.086 Attraktivität
Standardisiertes Modell:
Verkäufe = 0.511 Werbung + 0.512 Radiohäufigkeit +
0.192 Attraktivität
Standardabweichungen:
- Verkäufe: 80.699
- Werbung: 485.655
- Radiohäufigkeit: 12.27
- Attraktivität: 1.395
♪♫ Interpretation der Koeffizienten
Modell:
Verkäufe = -26.613 + 0.085 Werbung + 3.367 Radiohäufigkeit +
11.086 AttraktivitätStandardisiertes Modell:
Verkäufe = 0.511 Werbung + 0.512 Radiohäufigkeit +
0.192 Attraktivität
Klassische Koeffizienten \(b_i\):
Werbung: Wenn Werbung um eine Einheit (= 1000 £) erhöht ist, beobachtet man eine Erhöhung der Albumverkäufe um 0.085 Einheiten (entspricht 85 Stück).
Radiohäufigkeit: Wenn das Album um eine Einheit (= 1000 mal pro Woche) häufiger im Radio gespielt wird, beobachtet man eine Erhöhung der Albumverkäufe um 3.367 Einheiten (entspricht 3367 Stück).
Attraktivität: Wenn die Attraktivität um eine Einheit höher eingeschätzt wird, beobachtet man eine Erhöhung der Albumverkäufe um 11.086 Einheiten (entspricht 11086 Stück).
Standardisierte Koeffizienten \(\beta_i\):
Werbung: Wenn Werbung um eine Standardabweichung (= 485.655 [1000 £]) erhöht ist, beobachtet man eine Erhöhung der Albumverkäufe um 0.511 Standardabweichungen (entspricht 41225 Stück).
Radiohäufigkeit: Wenn das Album um eine Standardabweichung (= 12.27 [1000 pro Woche]) häufiger im Radio gespielt wird, beobachtet man eine Erhöhung der Albumverkäufe um 0.512 Standardabweichungen (entspricht 41317 Stück).
Attraktivität: Wenn die Attraktivität um eine Standardabweichung (= 1.395) höher eingeschätzt wird, beobachtet man eine Erhöhung der Albumverkäufe um 0.192 Standardabweichungen (entspricht 15469 Stück).
Standardabweichungen:
- Verkäufe: 80.699
- Werbung: 485.655
- Radiohäufigkeit: 12.27
- Attraktivität: 1.395
Voraussetzungen (multipel)
- Alle Annahmen der einfachen linearen Regressionsanalyse: Voraussetzungen
- Zusätzlich: Keine lineare Abhängigkeit zwischen den Prädiktoren (also keine Multikollinearität)
- Bestimmung von Variance Inflation Factor (VIF)
- \({\operatorname {VIF}_{j}={\frac {1}{1-R_{j}^{2}}}}\), mit \(R_{j}^{2}\) als Bestimmtheitsmaß der Regression von \(x_{j}\) auf alle übrigen Einflussgrößen (also außer \(x_{j}\)!)
- Kriterium: VIF < 10
- Beispiel ♪♫ – Modell 3: Korrelationsmatrix & VIF
Werbungen Radiohäufigkeit Attraktivität
Werbungen 1.00000000 0.1018828 0.08075151
Radiohäufigkeit 0.10188281 1.0000000 0.18198863
Attraktivität 0.08075151 0.1819886 1.00000000 Werbung Radiohäufigkeit Attraktivität
1.014593 1.042504 1.038455 Kreuzvalidierung
Kreuzvalidierung: Ansätze
Gretchenfrage: Gilt mein Modell auch für andere Stichproben – kann es generalisiert werden?
- Adjustiertes Bestimmtheitsmaß: \[R^2_{adj} = 1 - (1-R^2)(\frac{n-1}{n-k-1})\] (oder äquivalent: \(R^2_{adj} = 1 - \frac{MQS_{res}}{MQS_{tot}}\))
mit
n: Stichprobengröße
k: Anzahl Prädiktoren
R²: nicht-adjustiertes Bestimmtheitsmaß
Stichprobenaufteilung (sample splitting):
- Zufällige Aufteilung der Stichprobe 80 : 20
- Erstellen des linearen Modells für die 80 %
- Bestimmen von R²\(_{80\%}\)
- Anwendung des Modells auf die restlichen 20 %
- Bestimmen von R²\(_{20\%}\)
- Vergleich von R²\(_{80\%}\) und R²\(_{20\%}\)
Weitere Validierungsansätze (alle etwas aufwändiger):
- k-facher Kreuzvalidierungsansatz
- Leave One Out (LOOCV)
- Wiederholter k-facher Kreuzvalidierungsansatz
Beispiel Sample Splitting
(Zufällige Aufteilung ca. 80 : 20)
Ergebnis Trainingsmodell (ca. 80 %)
Call:
lm(formula = Verkäufe ~ Werbungen + Radiohäufigkeit + Attraktivität,
data = df_train)
Residuals:
Min 1Q Median 3Q Max
-128.535 -26.007 -0.525 27.483 140.963
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -36.720448 19.099229 -1.923 0.056339 .
Werbungen 0.084041 0.007366 11.409 < 2e-16 ***
Radiohäufigkeit 3.724373 0.325565 11.440 < 2e-16 ***
Attraktivität 10.887296 2.762561 3.941 0.000122 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 46.72 on 157 degrees of freedom
Multiple R-squared: 0.6888, Adjusted R-squared: 0.6829
F-statistic: 115.8 on 3 and 157 DF, p-value: < 2.2e-16Vergleich mit Test-Stichprobe (20 %):
R²\(_{80\%}\) = 0.69
R²\(_{20\%}\) = 0.57
- Zufällige Aufteilung der Stichprobe 80 : 20
- Erstellen des linearen Modells für die 80 %
- Bestimmen von R²\(_{80\%}\)
- Anwendung des Modells auf die restlichen 20 %
- Bestimmen von R²\(_{20\%}\)
- Vergleich von R²\(_{80\%}\) und R²\(_{20\%}\)
