Aufgabenblatt ANOVA mit MW

1 Aufgabe

Wir haben dasselbe Experiment vorliegen, das wir in der VL besprochen haben: unseren Welpen-Versuch; aber mit anderen Daten.

Ihre Aufgabe: Füllen Sie die Lücken!

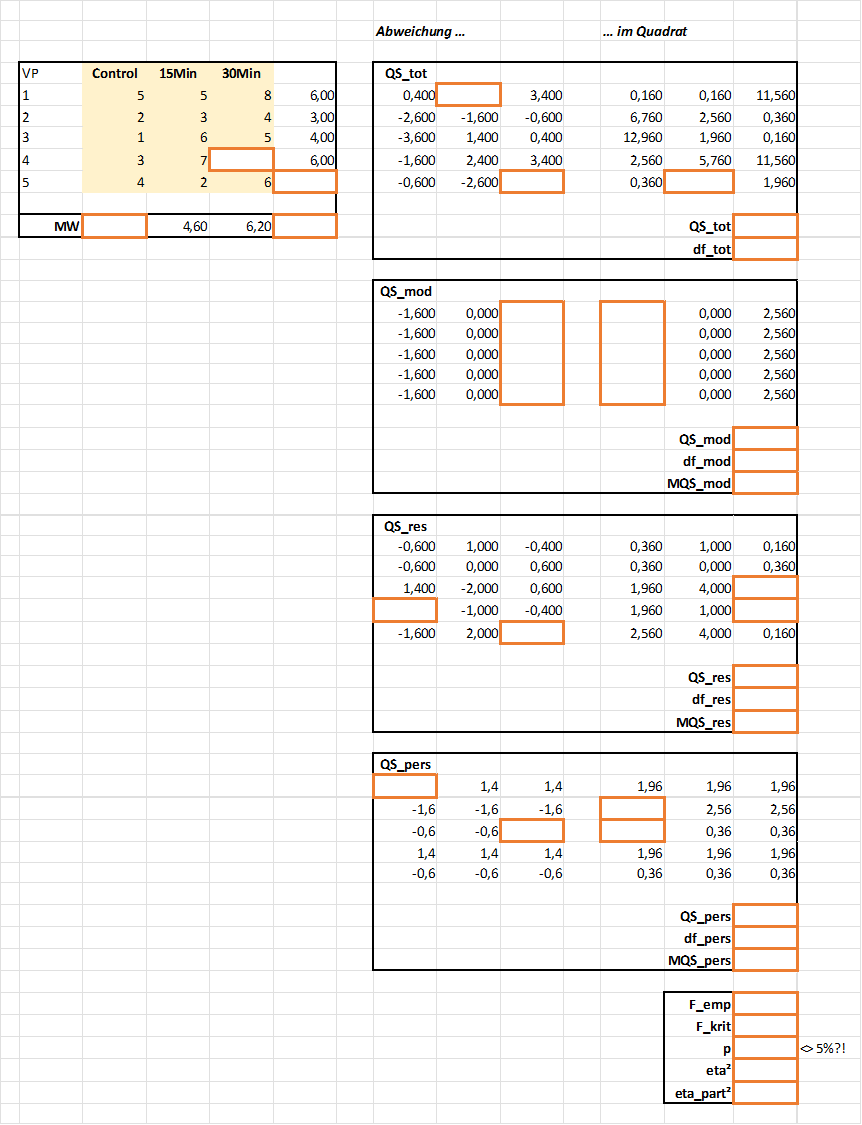
2 Aufgabe

Folgende Situation: Drei Erzieher:innen eines Kindergartens sollen anhand einer Skala von 0 bis 100 für 5 ihrer Schützlinge beurteilen, inwieweit deren Sozialverhalten für einen Übertritt auf die Grundschule schon ausreichend entwickelt ist. Dabei steht der Wert 0 für „noch gar nicht“ und 100 für „vollständig“. Ziel ist es, ein möglichst zuverlässiges Bild der sozialen Reife der Kinder zu erhalten.

Die Daten sehen so aus:

   person rater score
1       1     1    85
2       1     2    80
3       1     3    82
4       2     1    78
5       2     2    79
6       2     3    77
7       3     1    90
8       3     2    92
9       3     3    91
10      4     1    70
11      4     2    68
12      4     3    69
13      5     1    88
14      5     2    86
15      5     3    87

Die Datenstruktur entspricht unserem Beispiel aus der obigen Aufgabe. Hier sind die Kinder quasi die Versuchspersonen. Die einzelnen Erzieher:innen stehen für die Faktorstufen bzw. Arten des Treatments. Wir erhalten eine Matrix mit fünf Zeilen und drei Spalten (verwechseln Sie das nicht mit dem dargestellten DataFrame; der hat zwar auch drei Spalten, bei ihm sind aber alle Bewertungen in einer Spalte). In den Zellen der 5 x 3 Matrix finden wir die Bewertungen (0 bis 100). Skizzieren Sie das Beispiel in Matrix-Form auf Papier oder in Excel.

Ergänzen Sie eine 6. Zeile mit den Mittelwerten über die Kinder hinweg. Diese stellen die durchschnittliche Bewertung durch die drei Erzieher:innen dar. Ergänzen Sie ebenso eine weitere Spalte mit den Mittelwerten jedes Kindes über die drei Erzieher:innen hinweg. Ganz rechts unten finden wir wie gewohnt unseren totalen Mittelwert – über alle Kinder und Erzieher:innen.

1. Angenommen, wir berechnen eine ANOVA mit Messwiederholung. Was bedeutet dann ein signifikanter Omnibus-F-Test?

2. Bewerten Sie das Ergebnis eines signifikanten F-Wertes (mit unseren Daten nicht der Fall!). War dieser Unterschied das angestrebte Ziel der Studie – was vermuten Sie?

3. Angenommen, die Erzieher:innen kommen zu sehr ähnlichen Bewertungen (man könnte damit sagen: Sie sind also ähnlich kalibrierte Messinstrumente). Was erwarten Sie hinsichtlich der \(QS_{mod}\) und dem F-Wert?

4. Wie könnten wir überprüfen, wie gut die Erzieher:innen in ihren Bewertungen übereinstimmen (also anders als durch eine ANOVA, die ja testet, ob sie sich unterscheiden)?