Satz von Bayes

1 Beispiel zur Einführung relevanter Konzepte

Beispiel Würfeln. Betrachten wir zwei mögliche Ereignisse (= Mengen von Ergebnissen) eines Wurfes: (A) “Die Augenzahl ist kleiner als 4” und (B) “Die Augenzahl ist größer als 2”. Diese beiden Ereignisse können wir als Mengen darstellen: Menge A und Menge B. Element 3 ist Teil beider Mengen - liegt also in ihrem Schnittbereich.

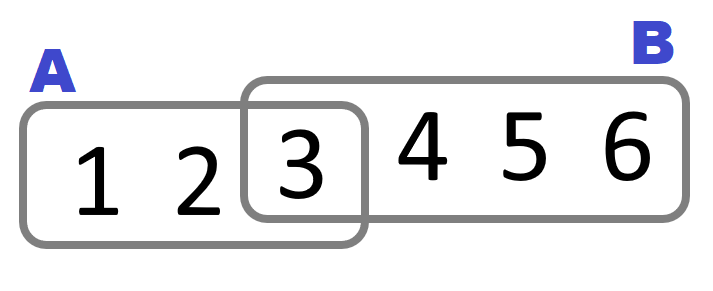
Für dieses Beispiel können wir folgende Notation festlegen:

• Wahrscheinlichkeit von Ereignis A: \(P(A) = \frac{1}{2}\)

• Wahrscheinlichkeit von Ereignis B: \(P(B) = \frac{2}{3}\)

• Wahrscheinlichkeit von Ereignis A UND Ereignis B: \(P(A ∩ B) = \frac{1}{6}\)

• Wahrscheinlichkeit von Ereignis A unter der Bedingung, dass Ereignis B bereits bekannt ist: \(P(A|B) = \frac{P(A \cap B)}{P(B)} = \frac{1/6}{2/3} = \frac{1}{4}\)

• Wahrscheinlichkeit von Ereignis B unter der Bedingung, dass Ereignis A bereits bekannt ist: \(P(B|A) = \frac{P(A \cap B)}{P(A)} = \frac{1/6}{1/2} = \frac{1}{3}\)

2 Hintergrund und Bedeutung

Der Satz von Bayes beschreibt, wie man die Wahrscheinlichkeit eines Ereignisses einschätzt, nachdem neue Informationen hinzugekommen sind. In der Psychologie hilft es, Prozesse der Wahrnehmung, Entscheidungsfindung und Urteilsbildung besser zu verstehen.

Bedeutung für Entscheidungs- und Wahrnehmungspsychologie:

• Urteilsbildung: Bayes verdeutlicht, wie Menschen Informationen verarbeiten und Urteile bilden.
• Wahrnehmungspsychologie: Hilft zu verstehen, wie Wahrnehmungen und Erwartungen interagieren.
• Kognitive Verzerrungen: Erklärt, warum Menschen manchmal zu fehlerhaften Einschätzungen kommen, indem sie Basisraten (Prior-Wahrscheinlichkeiten) ignorieren oder überschätzen.

Die folgenden psychologischen Themen haben einen Bezug zu Bayes: #TheDress, die Hollow Mask Illusion, die Bayesian Brain Hypothese, Predictive Processing & Autismus-Schizophrenie-Spektrum

3 Formel von Bayes

Die allgemeine Formel lautet:

\[ P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} \]

Dabei gilt:

• P(A|B): Wahrscheinlichkeit von A, gegeben B (A-Posteriori-Wahrscheinlichkeit; Posterior)
  
• P(B|A): Wahrscheinlichkeit von B, gegeben A (Likelihood)
  
• P(A): Wahrscheinlichkeit von A, bevor man die Information über B erhält (A-Priori-Wahrscheinlichkeit; Prior)
  
• P(B): Wahrscheinlichkeit von B insgesamt (Evidenz)

Wir können für unser Würfelbeispiel leicht feststellen, dass die Formel “stimmt” – also zum richtigen Ergebnis führt. Setzen Sie einfach die Zahlenwerte ein.

Im Kontext der Modellbildung und des Testens von Hypothesen wird die Formel häufig mit anderen Buchstaben formuliert, wobei H für eine Modellannahme steht (die Hypothese) und D für die Daten, die zu einer Hypothese mehr oder weniger gut passen. Diese mehr oder weniger gute Passung steckt in der Likelihood \(P(D|H)\):

\[ P(H|D) = \frac{P(D|H) \cdot P(H)}{P(D)} \]

4 Herleitung der Formel

Ausgangspunkt ist die Definition der bedingten Wahrscheinlichkeit:

\[ P(A|B) = \frac{P(A \cap B)}{P(B)} \]

Ebenso gilt:

\[ P(B|A) = \frac{P(A \cap B)}{P(A)} \quad \Rightarrow \quad P(A \cap B) = P(B|A) \cdot P(A) \]

Einsetzen dieser Gleichung in die erste ergibt:

\[ P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} \]

5 Anwendung

Der Satz von Bayes erlaubt es, die Wahrscheinlichkeit einer Erkrankung nach einem positiven Testergebnis zu berechnen – also z. B. die Wahrscheinlichkeit, dass eine Frau tatsächlich Brustkrebs hat, wenn der Mammographie-Test positiv ist.

\[ P(H|D) = \frac{P(D|H) \cdot P(H)}{P(D)} \]

• P(H|D): Wahrscheinlichkeit für Krebs bei positivem Test
• P(D|H): Wahrscheinlichkeit für positiven Test bei Krebs (Sensitivität)
• P(H): Prävalenz (Erkrankungshäufigkeit in der Bevölkerung)
• P(D): Gesamtwahrscheinlichkeit eines positiven Tests

6 Beispiel mit realistischen Zahlen

Die Werte basieren auf typischen Lehrbuchdaten:

• Prävalenz \(P(H) = 0{,}01\) (1 % der Frauen haben Brustkrebs)
• Sensitivität \(P(D \mid H) = 0{,}90\)
• Spezifität \(= 0{,}93\) \(\Rightarrow\) Falsch-Positiv-Rate \(= 1 - 0{,}93 = 0{,}07\)

\[ P(H | D) = \frac{0{,}90 \cdot 0{,}01}{0{,}90 \cdot 0{,}01 + 0{,}07 \cdot 0{,}99} = \frac{0{,}009}{0{,}009 + 0{,}0693} \approx 0{,}115 \]

7 Vereinfachte Berechnung mit absoluten Häufigkeiten

Wir berechnen die bedingte Wahrscheinlichkeit nicht mit Formeln, sondern durch systematisches Zählen anhand einer angenommenen Stichprobe von 10.000 Frauen.

7.1 Schritt 1: Erkrankte Frauen

• 1 % von 10.000 → 100 Frauen haben Brustkrebs
• 90 % davon werden erkannt (Sensitivität) → 90 erhalten ein positives Testergebnis

7.2 Schritt 2: Gesunde Frauen

• 99 % von 10.000 → 9.900 Frauen haben keinen Brustkrebs
• 7 % davon erhalten fälschlich ein positives Ergebnis → 693 falsch-positive Tests

7.3 Schritt 3: Gesamtzahl positiver Tests

• 90 echt positive Tests (krank & Test positiv)
• 693 falsch positive Tests (gesund & Test positiv)
• Total: 783 positive Tests

7.4 Schritt 4: Anteil echter Positiver

Die entscheidende Frage lautet: Wie viele der 783 positiv getesteten Frauen haben wirklich Brustkrebs?

\[ \frac{90}{783} \approx 0{,}115 = 11{,}5\% \]

7.5 Fazit

Trotz guter Sensitivität und Spezifität liegt die Wahrscheinlichkeit, bei positivem Testergebnis tatsächlich an Brustkrebs erkrankt zu sein, nur bei etwa 11,5 %. Der Grund ist die geringe Prävalenz in der untersuchten Population.

Merke: Selbst gute Tests liefern bei seltenen Krankheiten viele falsch-positive Ergebnisse.

8 Aufgaben mit Lösung

8.1 Monty Hall

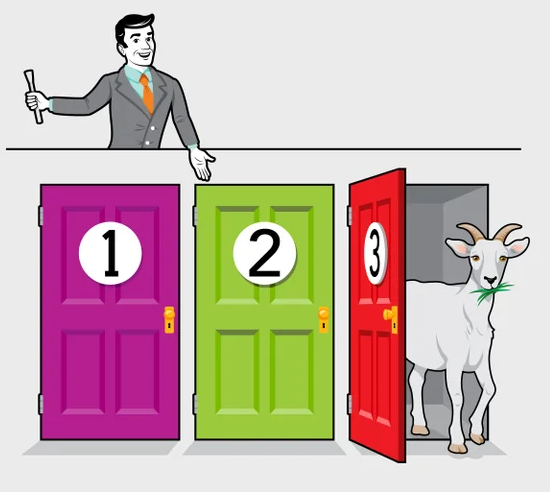
Lösen Sie das Monty-Hall-Problem mit Hilfe des Satzes von Bayes!

Hintergrund: Versetzen Sie sich in die folgende Situation. Sie nehmen an einer Quizshow teil. Der Moderator – Monty Hall – bietet Ihnen drei Türen zur Auswahl. Hinter zwei verbirgt sich jeweils eine Ziege. Das sind die Nieten. Hinter einer ist ein Auto. Wählen Sie 1, 2 oder 3. Die Wahrscheinlichkeit, dass dahinter das Auto steht, ist für jede Tür gleich hoch.

Nach Ihrer Wahl öffnet Hall eine der beiden Türen mit einer Ziege. Wir können davon ausgehen, dass er zufällig zwischen den beiden Ziegen wählt.

Monty Hall stellt Ihnen nun die entscheidende Frage: “Wollen Sie Ihre Wahl ändern?” – Sie haben nun also die Gelegenheit, statt der vorher von Ihnen gewählten Tür die andere noch geschlossene Tür zu wählen.

Sollten Sie das tun? Ändert sich die Wahrscheinlichkeit dafür, das Auto zu bekommen?

Lösung

Die folgende Lösung gilt unabhängig davon, welche Tür Sie und anschließend Monty Hall wählen.

Angenommen, Sie wählen Tür 1 und Hall öffnet anschließend Tür 2 mit einer Ziege. Wie hoch ist die Wahscheinlichkeit auf das Auto bei Tür 1 und bei Tür 3? Anders formuliert: Sollten Sie von Tür 1 zu 3 wechseln?

Die relevanten Bestandteile:

• “Auto hinter Tür 1”: P(A=1) = \(\frac{1}{3}\) (analog bei den beiden Türen)
• Gesucht wird P(A=1 | “Hall öffnet Tür 2”): P(A=1 | H=2)
• Gesucht wird außerdem P(A=3 | “Hall öffnet Tür 2”): P(A=3 | H=2)

Lösen wir mit Hilfe von Bayes:

\[ \small \begin{align*} P(A=1 | H=2) &= \frac{P(H=2 | A=1)P(A=1)}{P(H=2)} \\ &= \frac{P(H=2 | A=1)P(A=1)}{P(H=2 | A=1)P(A=1) + P(H=2 | A=2)P(A=2) + P(H=2 | A=3)P(A=3)} \\ &= \frac{(1/2)(1/3)}{(1/2)(1/3) + 0(1/3) + 1(1/3)} \\ &= \frac{1/6}{3/6} \\ &= \frac{1}{3} \end{align*} \] \[ \small \begin{align*} P(A=3 | H=2) &= \frac{P(H=2 | A=3)P(A=3)}{P(H=2)} \\ &= \frac{P(H=2 | A=3)P(A=3)}{P(H=2 | A=1)P(A=1) + P(H=2 | A=2)P(A=2) + P(H=2 | A=3)P(A=3)} \\ &= \frac{1(1/3)}{(1/2)(1/3) + 0(1/3) + 1(1/3)} \\ &= \frac{1/3}{3/6} \\ &= \frac{2}{3} \end{align*} \] Damit erhalten wir das nicht intuitive Ergebnis: Sie sollten die Tür wechseln! Damit verdoppeln Sie Ihre Gewinnchance.

8.2 Taxi-Problem

Vollziehen Sie das Taxi-Problem (SD/LD Kap. 16) mit Hilfe des Satzes von Bayes nach.

\[ \small \begin{align*} P(B) &= 0.15 \\ P(G) &= 0.85 \\ \\ P(´B´|B) &= 0.8 \\ P(´B´|G) &= 0.2 \\ \\ P(´G´|G) &= 0.8 \\ P(´G´|B) &= 0.2 \\ \\ P(B|´B´) &= \frac{P(´B´|B)P(B)}{P(´B´)} \\ &= \frac{P(´B´|B)P(B)}{P(´B´|B)P(B) + P(´B´|G)P(G)} \\ \\ &= \frac{0.8 \cdot 0.15}{0.8 \cdot 0.15 + 0.2 \cdot 0.85} \\ \\ & \approx \text{\large 41.3 \% } \end{align*} \]