Rozdział 2 Regresja
2.1 Model regresji liniowej – założenia
Modelem w statystyce często określamy założenie, że dane w próbce zostały wygenerowane przez proces probabilistyczny należący do określonej grupy procesów1.
Model regresji liniowej zakłada, że sposób, w jaki dane zostały wygenerowane, można opisać następującym równaniem:
\[y_i = \beta_0 + \beta_1 \cdot x_i + \varepsilon_i, \tag{2.1}\]
w przypadku regresji prostej (gdy jest tylko jedna zmienna objaśniająca)
lub następującym:
\[y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \dots + \beta_k x_{ik} + \varepsilon_i, \tag{2.2}\]
gdy zmiennych objaśniających jest \(k\) (więcej niż jedna, \(k>1\)) – regresja wieloraka.
Zakłada się więc, że relacja pomiędzy zmiennymi objaśniającymi (oznaczanymi literą X) i zmienną objaśnianą (oznaczaną literą Y) jest liniowa.
W równaniach modelu regresji pojawia się składnik losowy \(\varepsilon_i\) (nazywany „błędem” albo „zakłóceniem”), co do którego typowe założenia są następujące2:
jego wartość oczekiwana wynosi zawsze zero: \(\mathbb{E}(\varepsilon_i)=0\),
jego wariancja jest stała (nie zależy od X ani od niczego innego) i wynosi \(\sigma_\varepsilon^2\) (założenie stałej wariancji w tym kontekście nazywa się homoskedastycznością3),
jego wartości są generowane bez autokorelacji (czyli wartość składnika losowego dla dowolnej obserwacji \(i\) nie jest skorelowana z wartością składnika losowego dla dowolnej innej obserwacji \(j\)),
jego wartości mają rozkład normalny (rozkład Gaussa).
W efekcie, klasyczny model regresji liniowej sprowadza się do tego, że rozkład warunkowy \(Y_i|\left(X_1=x_{i1}, X_2=x_{i2}, \dots X_k=x_{ik}\right)\) jest rozkładem Gaussa o wartości oczekiwanej równej
\[\mu_{y_i} = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \dots + \beta_k x_{ik} \tag{2.3}\]
i odchyleniu standardowym równym \(\sigma_\varepsilon\).
Zapisujemy to w następujący sposób:
\[ Y_i|\left(X_1=x_{i1}, \dots X_k=x_{ik}\right) \sim \mathcal{N}\left(\beta_0 + \beta_1 x_{i1} + \dots + \beta_k x_{ik};\: \sigma_{\varepsilon}^2\right) \tag{2.4}\]
Rysunek 2.1: Model regresji to model warunkowego rozkładu zmiennej objaśnianej – przykład wykorzystujący symulowaną zależność między liczbą godzin nauki a wynikiem egzaminu
2.2 Model regresji liniowej – estymacja
Wartości \(\beta_0\), \(\beta_1\), …, \(\beta_k\) oraz \(\sigma_\varepsilon\) są nieobserwowanymi wprost parametrami procesu generującego dane („populacji”), możemy je oszacować na podstawie próbki losowej.
W przypadku klasycznego modelu regresji liniowej współczynniki \(\beta\) szacuje się za pomocą estymatora najmniejszych kwadratów.
Dla regresji prostej estymator współczynnik nachylenia linii regresji (\(\beta_1\)) można przedstawić w następującej formie:
\[ \widehat{\beta}_1 = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n} (x_i - \bar{x})^2}, \tag{2.5} \]
zaś wzór na estymator wyrazu wolnego to:
\[ \widehat{\beta}_0 = \bar{y} - \widehat{\beta}_1 \bar{x}. \tag{2.6} \]
Dla regresji wielorakiej estymator najmniejszych kwadratów ma w zapisie macierzowym następującą formę:
\[\widehat{\boldsymbol{\beta}}=\left(\mathbf{X}^\top\mathbf{X}\right)^{-1}\mathbf{X}^\top \mathbf{y}, \tag{2.7} \]
gdzie \(\widehat{\boldsymbol{\beta}}\) to wektor kolumnowy oszacowań współczynników \(\beta_1, \dots, \beta_k\) (\(k\) to liczba zmiennych objaśniających), \(\mathbf{X}\) to macierz układu, czyli macierz z wierszami odpowiadającymi poszczególnym obserwacjom i z kolumnami odpowiadającymi poszczególnym zmiennym objaśniającym (z kolumną jedynek odpowiadającą wyrazowi wolnemu), a \(\mathbf{y}\) to wektor kolumnowy z wartościami zmiennej objaśnianej.
Parametr \(\sigma\) szacuje się natomiast za pomocą następującego wzoru:
\[ \widehat{\sigma}_\varepsilon = \sqrt{\widehat{\sigma}_\varepsilon^2} \tag{2.8} \]
\[ \widehat{\sigma}_\varepsilon^2 = \frac{\sum_i(y_i-\hat{y}_i)^2}{n-k-1} \tag{2.9} \]
Estymację przeprowadza się zwykle z wykorzystaniem oprogramowania.
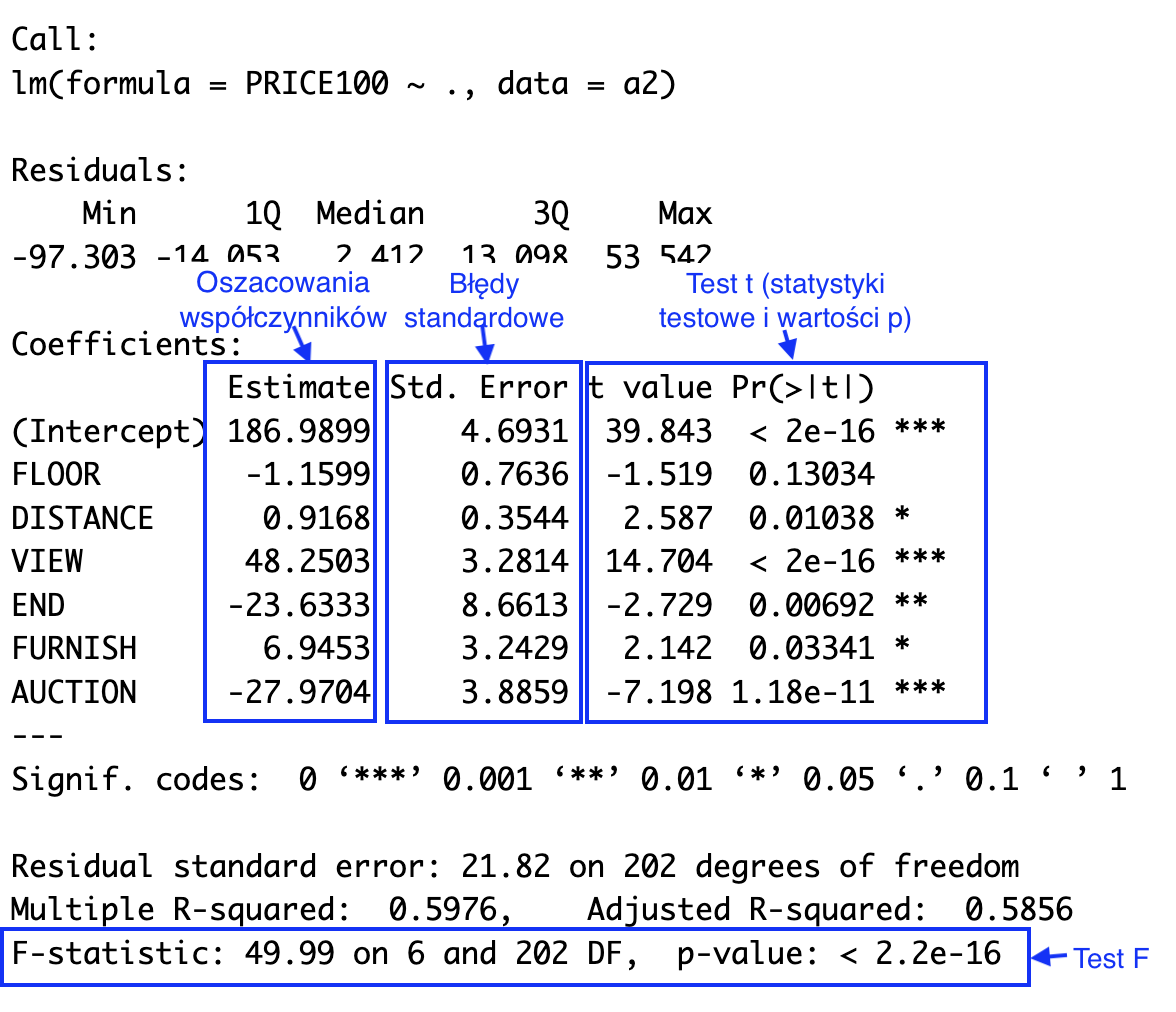
Rysunek 2.2: Typowe podsumowanie modelu regresji liniowej w R
2.2.1 Przedziały ufności dla współczynników modelu
Przedział ufności dla współczynnika modelu \(\beta_j\) (\(j = 1, 2, \dots, p\)) możemy wyznaczyć, korzystając z następującego wzoru.
\[\widehat{\beta}_j \pm t_{\alpha/2} \cdot \widehat{SE}(\widehat{\beta}_j), \tag{2.10}\]
gdzie \(\hat{\beta_j}\) to oszacowanie punktowe współczynnika \(\beta_j\), \(\widehat{SE}(\widehat{\beta}_j)\) to oszacowany błąd standardowy estymatora tego współczynnika, zaś wartość \(t_{\alpha/2}\) to odpowiedni kwantyl z rozkładu t-Studenta o \(n - p - 1\) stopniach swobody (\(n\) to liczba obserwacji w próbie, a \(p\) to liczba zmiennych objaśniających).
Wzory umożliwiające wyznaczenie błędu standardowego dla regresji prostej są następujące. Dla współczynnika nachylenia linii regresji (\(\beta_1\)):
\[ \widehat{SE}(\widehat{\beta}_1) = \frac{\widehat{\sigma}_\varepsilon}{\sqrt{\sum_i (x_i - \bar{x})^2}} \tag{2.11}\]
a dla wyrazu wolnego (punktu przecięcia):
\[ \widehat{SE}(\widehat{\beta}_0) = \widehat{\sigma}_\varepsilon \sqrt{\frac{1}{n} + \frac{\bar{x}^2}{\sum_i (x_i - \bar{x})^2}} \tag{2.12}\]
W przypadku regresji wielorakiej oszacowania błędów standardowych uzyskujemy dzięki następującego wzoru wykorzystującego algebrę macierzy.
\[\widehat{SE}(\widehat{\beta}_j) = \widehat{\sigma}_\varepsilon \sqrt{\left[\left( \mathbf{X}^\top\mathbf{X}\right)^{-1} \right]_{jj}}, \tag{2.13}\]
gdzie \(\mathbf{A}_{jj}\) oznacza element macierzy \(\mathbf{A}\) znajdujący się w \(j\)-tym wierszu w \(j\)-tej kolumnie.
W praktyce błędy standardowe są obliczane przez pakiety statystyczne.
2.2.2 Przedziały ufności dla wartości oczekiwanej zmiennej objaśnianej
Przedziały ufności dla warunkowej średniej (warunkowej wartości oczekiwanej) zmiennej objaśnianej przy ustalonych wartościach zmiennych objaśniających wyznaczamy na podstawie następującego wzoru:
\[\widehat{y}_h \pm t_{\alpha/2} \cdot \widehat{SE}(\widehat{y}_h), \tag{2.14}\]
gdzie \(x_{h1}, \dots, x_{hp}\) to ustalone wartości zmiennych objaśniających, z których można utworzyć wektor kolumnowy \(\mathbf{x}_h\), \(\hat{y}_h = \hat{\beta_0} + \hat{\beta_1} x_{h1} + \dots + \hat{\beta_k} x_{hk}\) to punktowe oszacowanie wartości oczekiwanej zmiennej \(Y\) w takiej sytuacji, zaś \(\widehat{SE}(\hat{y}_h)\) to szacunek jego błędu standardowego.
Dla regresji prostej:
\[ \widehat{SE}(\hat{y}_h) = \widehat{\sigma}_\varepsilon\sqrt{\frac{1}{n}+\frac{(x_h-\bar{x})^2}{\sum_i(x_i-\bar{x})^2}}, \tag{2.15} \]
zaś dla regresji wielorakiej:
\[\widehat{SE}(\hat{y}_h) = \widehat{\sigma}_\varepsilon\sqrt{\mathbf{x}_h^\top (\mathbf{X}^\top\mathbf{X})^{-1}\mathbf{x}_h}. \tag{2.16}\]
2.3 Przedziały predykcji
Zwykle jesteśmy zainteresowani nie tylko wartością oczekiwaną, ale również rozrzutem wokół tej wartości. Przedział predykcji uwzględnia obie te informacje, ponieważ stanowi oszacowanie zakresu wartości, w którym z ustalonym prawdopodobieństwem (równym \(1-\alpha\)) będzie się mieścić nowa pojedyncza obserwacja pochodząca z tej samej populacji (wygenerowana przez ten sam proces).
Dla regresji prostej przedział predykcji wyznaczamy za pomocą następującego wzoru:
\[ \hat{y}_h\pm t_{\alpha/2}\widehat{\sigma}_\varepsilon\sqrt{1+\frac{1}{n}+\frac{(x_h-\bar{x})^2}{\sum_i(x_i-\bar{x})^2}}, \tag{2.17} \]
gdzie \(\hat{y}_h\) to wartość oczekiwana zmiennej objaśnianej \(Y\) pod warunkiem, że zmienna objaśniająca X jest równa \(x_h\):
Dla regresji wielorakiej można zastosować następujący wzór macierzowy:
\[ \hat{y}_h\pm t_{\alpha/2}\widehat{\sigma}_\varepsilon\sqrt{1+\mathbf{x}_h^\top (\mathbf{X}^\top\mathbf{X})^{-1}\mathbf{x}_h} \tag{2.18} \]
2.4 Model regresji liniowej – test t i test F
Pakiety statystyczne (a nawet arkusze kalkulacyjne takie jak Excel) zwykle obliczają statystyki umożliwiające przeprowadzenie dwóch rodzajów testów dla regresji liniowej: testów istotności pojedynczych współczynników \(\beta_j\) („testów t”) oraz testu łącznej istotności modelu („testu F”).
2.4.1 Testy istotności współczynników
1. W teście t współczynnika \(\beta_j\) hipoteza zerowa zakłada, że jest on równy zero:
\[ H_0: \beta_j = 0 \] 2. Hipoteza alternatywna jest dwustronna:
\[ H_A: \beta_j \ne 0 \]
3. Statystykę testową t wyznacza się w następujący sposób:
\[t = \frac{\widehat{\beta}_j}{\widehat{SE}(\widehat{\beta}_j)} \tag{2.19} \]
Przy założeniu prawdziwości hipotezy zerowej statystyka testowa ma rozkład t z liczbą stopni swobody równą \(n-p-1\).
4. Obszar odrzucenia i p-value wyznacza się tak, jak w innych dwustronnych testach t.
2.4.2 Test F
1. W teście F hipoteza zerowa stwierdza, że wszystkie współczynniki przy zmiennych objaśniających są równe zero:
\[ H_0: \beta_1 = \dots = \beta_k = 0 \] Warto zauważyć, że hipoteza zerowa nie obejmuje wyrazu wolnego (\(\beta_0\)).
2. Hipoteza alternatywna stwierdza zaś, że przynajmniej jeden z nich jest różny od zera:
\[ H_A:\text {istnieje } j \in \{1, \dots, k\}\text{, takie że } \beta_j \ne 0 \]
3. Statystyka testowa ma rozkład F z liczbą stopni swobody w liczniku (\(df_1\)) równą \(k\) i liczbą stopni swobody w mianowniku (\(df_2\)) równą \(n - k - 1\).
\[F_{(k,n-k-1)}=\frac{SSR/k}{SSE/(n-k-1)}=\frac{\sum_{i=1}^n\left(\widehat{y}_i-\bar{y}\right)^2/k}{\sum_{i=1}^n\left(y_i-\widehat{y}_i\right)^2/({n-k-1})} \tag{2.20}\]
2.5 Ocena założeń modelu regresji
Ocena założeń modelu regresji to próba odpowiedzi na pytanie, czy przyjęta specyfikacja modelu jest odpowiednia. Klasyczny model regresji liniowej zakłada m.in. liniowość, stałość wariancji (homoskedastyczność), niezależność składnika losowego i rozkład normalny tego składnika. Kiedy założenia są w znacznym stopniu naruszone, wyniki analiz (np. przedziały predykcji, przedziały ufności, testy t istotności uzyskanych oszacowań) mogą wprowadzać w błąd.
Oceniając model regresji, należy pamiętać, że:
Praktycznie „wszystkie modele są błędne, ale niektóre są użyteczne”. Celem oceny założeń modelu nie jest udowodnienie prawdziwości założeń, ale ocena stopnia ich naruszenia.
Przed oceną stopnia naruszenia założeń na podstawie danych, należy najpierw rozważyć te założenia niezależnie od posiadanych danych (wykorzystując wiedzę merytoryczną o procesie generującym dane).
O ile to tylko możliwe, ocenie stopnia naruszenia założeń na podstawie danych powinny towarzyszyć metody graficzne i opisowe. Dobrą praktyką jest rozpoczęcie od zwykłego wykresu rozrzutu \((x_i, y_i)\) lub kilku takich wykresów, jeśli istnieje więcej zmiennych objaśniających \(X\). Takie wykresy mogą dać natychmiastowy wgląd w zasadność założeń dotyczących liniowości, stałej wariancji i normalności, a także pomóc w identyfikacji wartości odstających (outliers).
Ocena, czy założenia są naruszone w znacznym stopniu, może być wspomagana symulacją.
Testy statystyczne niekoniecznie odpowiadają na właściwe pytanie. Wartość p z testu dotyczącego założenia odpowiada jedynie na pytanie: „Czy zaobserwowany efekt można wytłumaczyć wyłącznie przypadkiem?”, nie odpowiada na pytanie: „Czy założenie jest spełnione?” ani na pytanie: „Czy założenie jest naruszone na tyle, że trzeba użyć innej metody?”. W sytuacji małej liczebności próby testy nie wykrywają dużych naruszeń, dla dużych prób z kolei testy wykrywają nawet minimalne odstępstwa od założeń. Testy diagnostyczne mogą pełnić więc jedynie rolę pomocniczą, rzadko będą mogły być jedynym kryterium, na podstawie podejmujemy decyzje.
2.5.1 Weryfikacja liniowości
Do wizualnej oceny odpowiedniości założenia o liniowości modelu można wykorzystać wykresy \((x_i, y_i)\) rozrzutu wartości zmiennej objaśnianej względem poszczególnych zmiennych objaśniających oraz wykresy \((x_i, \widehat{\varepsilon}_i)\) rozrzutu wartości reszt modelu względem tych zmiennych. Jeżeli liczba zmiennych objaśniających jest duża, bardzo użyteczny może być wykres \((\widehat{y}_i, \widehat{\varepsilon}_i)\) rozrzutu wartości dopasowanych i reszt modelu (predicted/residual scatterplot). Na wykresach warto dodać wygładzone linie trendu, np. przy użyciu metody LOESS, co ułatwia identyfikację ewentualnych nieliniowych zależności.
Chmury punktów (i krzywe LOESS) mocno odbiegające od prostej linii mogą stanowić przesłankę do odejścia od modelu liniowego. Należy jednak pamiętać, że wszystkie założenia nie dotyczą danych, ale odnoszą się do procesu generującego dane. Gdy chcemy twierdzić, że występuje krzywizna, powinna ona mieć sens w kontekście merytorycznym badania.
Wykresy \((x_i, y_i)\), \((x_i, \widehat{\varepsilon}_i)\) oraz \((\widehat{y}_i, \widehat{\varepsilon}_i)\) dla oszacowań modeli liniowych na danych symulowanych z dwóch procesów generujących dane:
Po lewej stronie z procesu liniowego: \[ y = 0{,}4x + \varepsilon; \: \varepsilon \sim \mathcal{N}(0; 0{,}05^2) \tag{2.21}\]
Po prawej stronie z procesu krzywoliniowego:
\[ y = 0{,}4x - 3x^2 + \varepsilon; \: \varepsilon \sim \mathcal{N}(0; 0{,}05^2) \tag{2.22}\]
set.seed(123)
n <- 120
x <- runif(n, -.15, .15)
#hist(x)
beta_0 <- 0
beta_1 <- .4
beta_2 <- (-3)
sigma_epsilon <- .05
y <- beta_0 + beta_1*x + rnorm(n, 0, sigma_epsilon)
model0 <- lm(y~x)
#par(mfrow=c(3,2), mar=c(5,5,0,0))
plot(x,y)
lines(lowess(x, y), col="red", lty=2, lwd=2)
abline(model0, col="blue")
y <- beta_0 + beta_1*x + beta_2*x^2 + rnorm(n, 0, sigma_epsilon)
modelk <- lm(y~x)
plot(x,y)
lines(lowess(x, y), col="red", lty=2, lwd=2)
abline(modelk, col="blue")
resid <- model0$residuals
plot(x, resid)
lines(lowess(x, resid), col="red", lty=2, lwd=2)
abline(h=0, col="blue")
resid <- modelk$residuals
plot(x,resid)
lines(lowess(x, resid), col="red", lty=2, lwd=2)
abline(h=0, col="blue")
yhat <- model0$fitted.values
resid <- model0$residuals
plot(yhat, resid)
lines(lowess(yhat, resid), col="red", lty=2, lwd=2)
abline(h=0, col="blue")
yhat <- modelk$fitted.values
resid <- modelk$residuals
plot(yhat,resid)
lines(lowess(yhat, resid), col="red", lty=2, lwd=2)
abline(h=0, col="blue")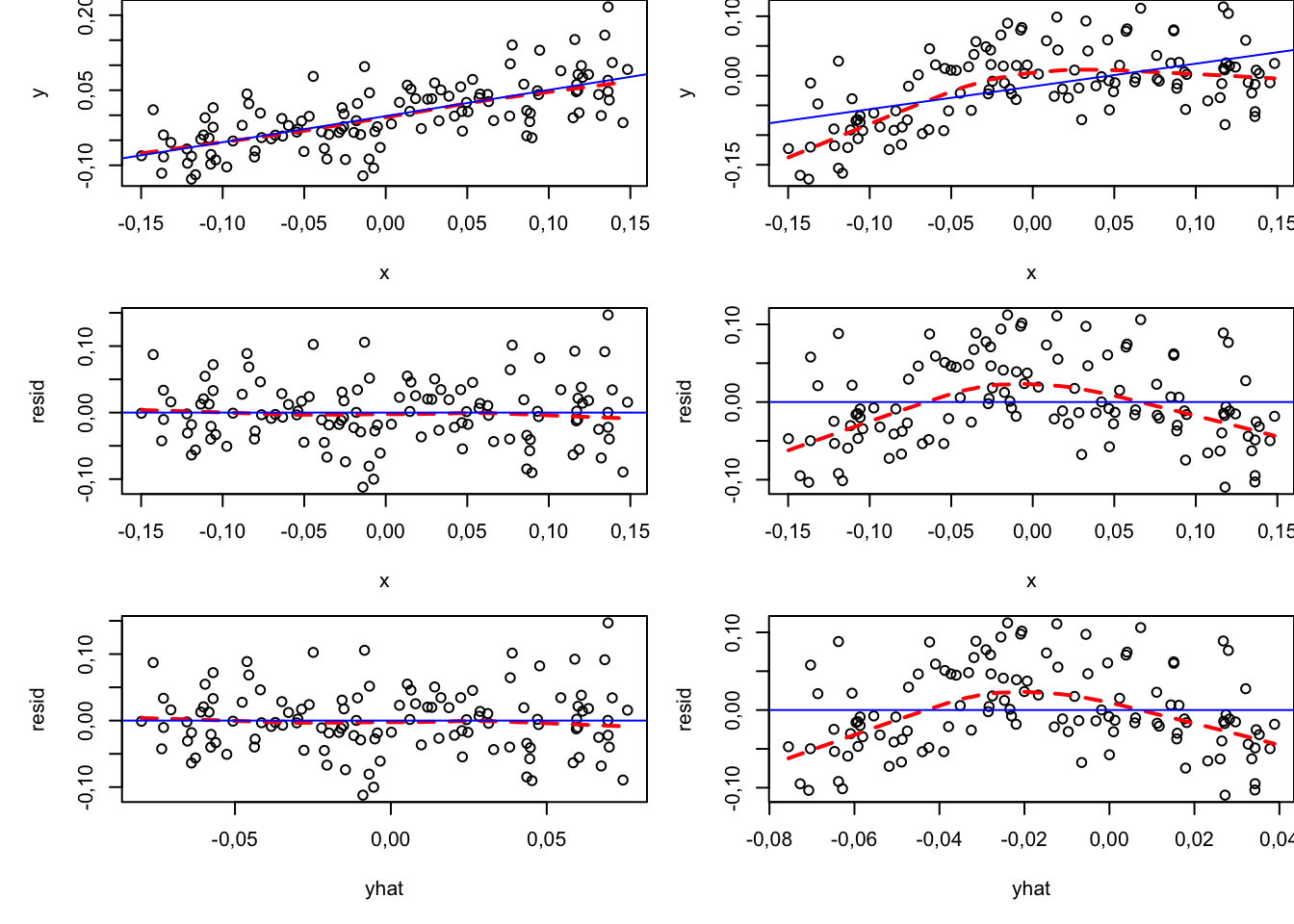
Przykładem testu stosowanego do oceny założenia o liniowości jest test RESET Ramseya.
W swojej domyślnej wersji w R (funkcja lmtest::resettest) test bazuje na porównaniu oszacowania modelu bazowego:
\[y = \beta x + \varepsilon \tag{2.23}\]
oraz oszacowania modelu opisanego równaniem (\(\widehat{y}\) to wartości dopasowane z modelu bazowego):
\[y = \beta_1 x + \beta_2 \widehat{y}^2 + \beta_3 \widehat{y}^3 + \varepsilon \tag{2.24}\]
Hipoteza zerowa w tym teście to \(H_0: \: \beta_2 = \beta_3 = 0\).
Wynik testu odpowiada na pytanie, na ile obserwowana w danych nieliniowość da się wytłumaczyć przypadkiem. Gdyby specyfikacja liniowa była prawdziwa, oszacowania \(\widehat{\beta}_2\) i \(\widehat{\beta}_3\) byłyby zbliżone do zera (przypadkowe uzyskanie wartości odległych od zera byłoby mało prawdopodobne). Z kolei gdyby rzeczywista zależność była krzywoliniowa (niekoniecznie miała postać funkcji sześciennej, praktyka pokazuje, że taki model może dopasować się do wielu krzywizn, test jest więc czuły dla wielu modeli nieliniowych), oszacowania byłyby „istotnie statystycznie” oddalone od zera.
Jeśli wynik testu jest istotny (p-value jest małe), nie oznacza to automatycznie, że należy przyjąć model zakrzywiony. Zamiast tego warto zadać sobie pytania: „Czy ta krzywizna jest na tyle wyraźna, by uzasadnić większą złożoność modelu?”, „Czy przewidywania istotnie się różnią między modelem z krzywizną a zwykłym modelem liniowym?”. Jeśli odpowiedź na te pytania brzmi „nie”, wówczas można pozostać przy modelu liniowym – nawet jeśli został on „odrzucony” na bazie p-value.
Na przykład model zakładający „normalność zmiennej X w populacji” oznacza założenie, że dane w próbce zostały wygenerowane z rozkładu Gaussa o średniej i odchyleniu standardowym, które możemy próbować oszacować.↩︎
Są to założenia typowe, klasyczne, najprostsze. W zależności od potrzeb buduje się modele, w których założenia dotyczące składnika losowego wyglądają inaczej. W tym skrypcie pojawi się na przykład wersja, w której rozkład składnika losowego nie jest rozkładem Gaussa.↩︎
Brak stałej wariancji to z kolei heteroskedastyczność↩︎