Rozdział 3 Miary tendencji centralnej i miary pozycyjne
3.1 Średnia
3.1.1 Średnia arytmetyczna
Średnia arytmetyczna to najprostsze i podstawowe narzędzie podsumowujące położenie rozkładu cechy. Jeżeli mówimy po prostu „średnia”, najczęściej chodzi nam właśnie o średnią arytmetyczną.
Średnia arytmetyczna z \(n\) wartości (oznaczanych od \(x_1\) do \(x_n\)) wynosi:
\[\begin{equation} \overline{x} = \frac{\sum_{i=1}^n x_i}{n} \tag{3.1} \end{equation}\]
Można powiedzieć, że średnia jest środkiem ciężkości zbioru danych.
Typowe własności:
Suma odchyleń \((\overline{x}-x_i)\) od średniej jest równa zero.
Średnia arytmetyczna to taka liczba, że suma kwadratów różnic między nią a każdą z wartości \(x_i\) (czyli następująca suma: \(\sum_i(x_i-\overline{x})^2\)) jest najmniejsza.
Jeżeli każdą z wartości \(x_i\) powiększymy o stałą \(a\), to nowa średnia wyniesie \(\overline{x}+a\).
Jeżeli każdą z wartości \(x_i\) pomnożymy przez stałą \(k\), to nowa średnia wyniesie \(k\overline{x}\).
3.1.2 Ważona średnia arytmetyczna
Niekiedy liczbom z opisywanego zbioru przypisujemy różne wagi (\(x_1\) uwzględniamy z wagą \(w_1\), \(x_2\) z wagą \(w_2\), itd.). Wagi powinny sumować się do jedności: \(\sum_i w_i=1\). Jeżeli mamy wagi \(w^*_i\), które nie sumują się do 1, można je sprowadzić do wag sumujących się do 1 za pomocą wzoru \(w_i = w^*_i / \sum_i w^*_i\).
Jeżeli wagi sumują się do 1, arytmetyczną średnią ważoną wyznaczamy na podstawie wzoru:
\[\overline{x}_{\text{ważona}} =\sum_{i=1}^n x_iw_i \tag{3.2}\]
Jeżeli wszystkie wagi są równe, arytmetyczna średnia ważona jest równa zwykłej średniej arytmetycznej.
Jeżeli nasze dane są w formie szeregu rodzielczego punktowego (zob. 2.1.2), można użyć średniej ważonej z wagami do wyznaczenia średniej arytmetycznej danych:
\[ \overline{x} =\frac{\sum_{j=1}^k x_j n_j}{n} \tag{3.3}\]
W powyższym wzorze \(x_j\) (\(j = 1, ..., k\)) to oznaczenia poszczególnych wartości (punktów danych), \(n_j\) to liczba wystąpień \(j\)-tej wartości, zaś \(n\) to łączna liczba obserwacji. Wagi w tym przypadku to \(w_j = n_j/n\).
3.1.3 Średnia harmoniczna
Średnią harmoniczną wyznaczamy za pomocą następującego wzoru:
\[ H = \frac{n}{\sum_{i=1}^n\frac{1}{x_i}} \tag{3.4}\]
Średnia harmoniczna może zapewnić właściwą średnią, jeżeli liczymy średnią z ilorazów, których licznik jest równy. Na przykład, jeżeli z miejsca A do miejsca B pojadę z prędkością 10 km/h, a wrócę tą samą trasą z prędkością 15 km/h, to moja średnia prędkość podróży będzie równa średniej harmonicznej z tych dwóch liczb (10 i 15) i będzie wynosiła 12 km/h.
Wzór na ważoną średnią harmoniczną (dla wag sumujących się do jedności):
\[ H_{\text{ważona}} = \frac{1}{\sum_{i=1}^n\frac{w_i}{x_i}} \tag{3.5}\]
3.1.4 Średnia geometryczna
Średnia geometryczna wyznaczana jest na podstawie wzoru:
\[ G = \left(x_1\cdot x_2\cdot ... \cdot x_n\right)^{1/n} = \left(\prod_i x_i\right)^{1/n}\]
Średnia geometryczną wykorzystujemy między innymi wyznaczając średnie tempo wzrostu.
Wzór na średnią geometryczną możemy również zapisać używając logarytmów i funkcji wykładniczej: \(\text{exp}(x) = e^x\):
\[ G = \text{exp} \left(\frac {1}{n}\sum \limits _{i=1}^{n}\ln x_{i}\right) \tag{3.6}\]
Możliwe jest też wyznaczenie ważonej średniej geometrycznej (wagi \(w_i\) sumują się do jedności):
\[ G = \text{exp} \left(\sum \limits _{i=1}^{n}w_i\ln x_{i}\right) \tag{3.7}\]
3.2 Mediana
Mediana dzieli dany zbiór (próbę, populację) na dwie równe części. Jeżeli posortujemy zbiór liczb, to mediana będzie środkową wartością lub, jeżeli nie ma jednej środkowej obserwacji, średnią arytmetyczną z dwóch środkowych wartości.
Mediana jest mniej wrażliwa na wartości odstające niż średnia arytmetyczna, dlatego lepiej opisuje tendencję centralną (wartość przeciętną) w zbiorze z dużymi skrajnościami i/lub asymetrycznym rozkładem wartości.
Nie jest potrzebna znajomość wszystkich wartości, żeby wyznaczyć medianę. Może to być ważne w analizie przeżycia (np. gdy mierzymy czas życia produktu lub klienta).
Mediana jest mniej wygodna niż średnia arytmetyczna obliczeniach matematycznych. Średnia arytmetyczna jest zwykle preferowana („lepsza” niż mediana) przy wnioskowaniu statystycznym, np. gdy chcemy poznać rozkład w populacji na podstawie próby losowej. Obliczenie mediany wymaga zazwyczaj więcej mocy obliczeniowej i pamięci komputera.
3.2.1 Wyznaczanie przybliżenia mediany z szeregu rozdzielczego przedziałowego
Jeśli mamy szereg rozdzielczy przedziałowy (czyli dane pogrupowane w przedziały klasowe z liczebnościami), to mediany nie można odczytać „dokładnie”, tylko trzeba ją przybliżyć interpolacją liniową. W takiej sytuacji można zastosować następujący wzór:
\[ Me = l_M + \left(\frac{n}{2}-n_{M-}\right)\frac{h_M}{n_M} \tag{3.8}\] gdzie:
\(n\) to liczebność badanej zbiorowości,
\(n_M\) to liczebność przedziału medianowego (zawierającego medianę),
\(h_M\) to szerokość przedziału medianowego,
\(l_M\) to dolna granica przedziału medianowego,
\(n_{M-}\) to skumulowana liczebność wszystkich przedziałów poniżej przedziału medianowego.
Warto pamiętać, że stosując taki wzór, w sposób niejawny zakłada się równomierny rozkład wartości wewnątrz przedziału klasowego.
3.3 Dominanta
Dominanta (moda, modalna) to wartość najczęściej występująca w zbiorze danych (szeregu liczb). Szereg może mieć kilka dominant. Dominantę można wyznaczać dla zmiennych ilościowych i jakościowych.
3.3.1 Wyznaczanie dominanty z szeregu rozdzielczego przedziałowego
Jeżeli liczby dotyczą cechy ciągłej, taka definicja dominanty traci rację bytu. W takich sytuacjach często stosuje się inną definicję dominanty: jest to miejsce na osi X, dla którego histogram (stworzony na podstawie szeregu rozdzielczego) osiąga szczyt. W takiej sytuacji dominanta zależy od sposobu pogrupowania danych w klasy oraz od szczegółowego sposobu wyznaczenia miejsca na osi X (środek przedziału lub interpolacja).
Interpolacyjny wzór umożliwiający wyznaczenie dominanty to:
\[ Mo = l_m + \frac{n_m - n_{m-1}}{(n_m - n_{m-1}) + (n_m - n_{m+1})} \cdot h \tag{3.9}\]
gdzie:
\(l_m\) to dolna granica przedziału modalnego (dominującego), czyli takiego, którego liczebność \(n_m\) jest największa,
\(n_m\) to liczebność przedziału modalnego,
\(n_{m-1}\) to liczebność przedziału poprzedzającego przedział modalny,
\(n_{m+1}\) to liczebność przedziału następującego po przedziale modalnym,
\(h\) to szerokość przedziałów.
Powyższy wzór zakłada, że wszystkie szerokości przedziałów \(h\) są równe. Jeżeli nie są równe, potrzebne jest wyznaczenie gęstości liczebności \(d_j=n_j/h_j\) w każdym przedziale \(j=1,2,3,...,k\). W takiej sytuacji wzór ma postać:
\[ Mo = l_m + \frac{d_m - d_{m-1}}{(d_m - d_{m-1}) + (d_m - d_{m+1})} \cdot h_m \tag{3.10}\]
gdzie:
\(l_m\) to dolna granica przedziału modalnego (dominującego), czyli takiego, którego gęstość liczebności \(d_m=n_m/h_m\) jest największa,
\(d_m\) to gęstość liczebności przedziału modalnego,
\(d_{m-1}=n_{m-1}/h_{m-1}\) to gęstość liczebności przedziału poprzedzającego przedział modalny,
\(d_{m+1}=n_{m+1}/h_{m+1}\) to gęstość liczebności przedziału następującego po przedziale modalnym,
\(h_m\) to szerokość przedziału modalnego.
Tak jak w przypadku innych wzorów umożliwiających szacowanie statystyk na bazie szeregu rozdzielczego przedziałowego, zakłada się w sposób niejawny się równomierny rozkład wartości wewnątrz przedziałów.
3.4 Miary pozycyjne (kwantyle)
Miary pozycyjne to miary oparte na uporządkowanym (posortowanym) zbiorze danych. Przykładem takiej miary jest najbardziej znany kwantyl: mediana.
3.4.1 Kwartyle
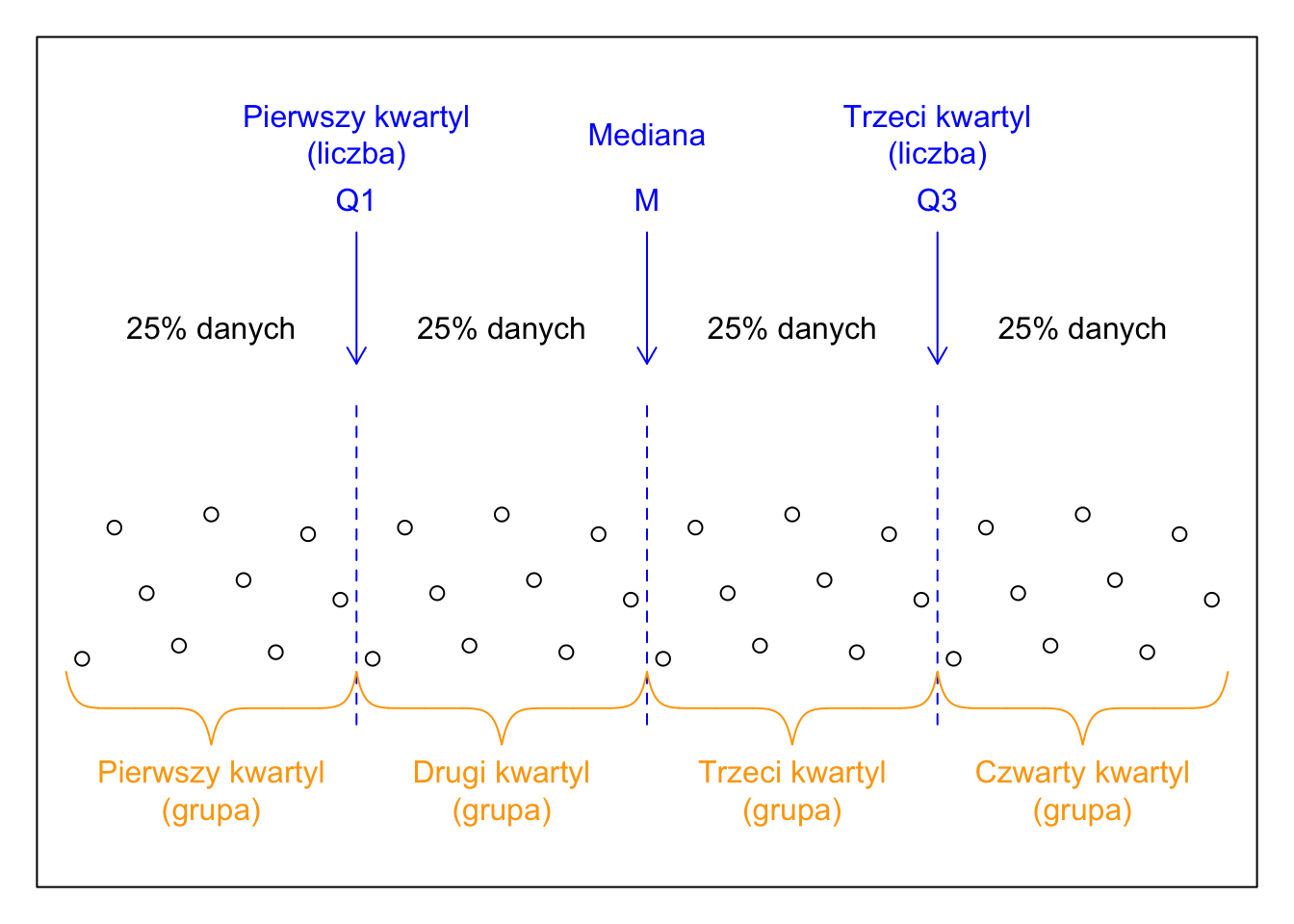
Mediana dzieli dany zbiór (próbę, populację) na dwie równe części. Kwartyle (pierwszy, drugi = mediana i trzeci) dzielą dany zbiór na cztery równe części.
Kwartyl pierwszy (dolny) to (w pierwszym znaczeniu, zob. niżej) liczba, która rozbija zbiór danych na dolne 25% obserwacji i górne 75% obserwacji.
Kwartyl drugi to mediana. Rozbija ona zbiór danych na dolne 50% i górne 50%.
Kwartyl trzeci (górny) to liczba, która rozbija zbiór na dolne 75% obserwacji i górne 25% obserwacji.
3.4.2 Dwa znaczenia słowa kwartyl
Warto przy tej okazji zwrócić uwagę na fakt, że słowo kwartyl (podobnie jak słowa oznaczające niektóre inne kwantyle, np. kwintyl lub decyl) może występować w dwóch znaczeniach:
w pierwszym znaczeniu kwartyl (kwintyl, decyl) to wartość liczbowa oddzielająca określoną frakcję (np. pierwszy kwartyl oddziela dolne 25% )
w drugim znaczeniu kwartyl to obserwacje, które pod względem analizowanej cechy znajdują się w określonej ćwiartce. Aby uniknąć niejednoznaczności, można użyć określenia „grupa kwartylowa”.
Na przykład weźmy dochód dyspozycyjny gospodarstw domowych. Drugi kwartyl to:
w pierwszym znaczeniu – mediana dochodów,
w drugim znaczeniu – te gospodarstwa domowe, których dochód znajduje się w przedziale między pierwszym kwartylem (w pierwszym znaczeniu) a medianą.
3.4.3 Kwintyle
Kwintyle dzielą zbiór danych na 5 grup, np. drugi kwintyl (w pierwszym znaczeniu) dzieli zbiór na dolne 40% i górne 60%.
3.4.4 Decyle
Decyle dzielą zbiór danych na 10 grup. Na przykład 3 decyl dzieli zbiór na dolne 30% i górne 70%.
3.4.5 Percentyle
Percentyle albo centyle dzielą zbiór danych na 100 grup. Przyjmuje się, że analogicznie można zdefiniować percentyle ułamkowe, np. percentyl 97,5 dzieli zbiór danych na dolne 97,5% i górne 2,5%.
3.4.6 Wyznaczanie kwantyli w praktyce
W praktyce okazuje się, że definicja przedstawiona powyżej nie jest wystarczająco jednoznaczna. Na przykład, czy da się wyznaczyć na podstawie ogólnej definicji pierwszy kwartyl dla zbioru danych składającego się z jedynie 11 obserwacji?
W poniższej tabeli pokazano wyznaczenie kwartyli dla prostego zbioru danych składającego się z dziesięciu liczb: 1, 1, 2, 2, 4, 5, 6, 7, 9, 10 z wykorzystaniem dziewięciu (!) algorytmów zaimplementowanych w R.
Nie wnikając w zawiłości algorytmów, warto zaznaczyć, że w R i w Excelu/Google (funkcja KWARTYL) domyślnie stosowany jest algorytm 7.
| Numer algorytmu | Kwartyl 1 | Mediana | Kwartyl 3 |
|---|---|---|---|
| type = 1 | 2.000000 | 4.0 | 7.000000 |
| type = 2 | 2.000000 | 4.5 | 7.000000 |
| type = 3 | 1.000000 | 4.0 | 7.000000 |
| type = 4 | 1.500000 | 4.0 | 6.500000 |
| type = 5 | 2.000000 | 4.5 | 7.000000 |
| type = 6 | 1.750000 | 4.5 | 7.500000 |
| type = 7 | 2.000000 | 4.5 | 6.750000 |
| type = 8 | 1.916667 | 4.5 | 7.166667 |
| type = 9 | 1.937500 | 4.5 | 7.125000 |
3.5 Linki
Średnia a mediana — aplikacja webowa: https://istats.shinyapps.io/MeanvsMedian/
Asymetria rozkładu a średnia i mediana — symulacja: https://college.cengage.com/nextbook/statistics/utts_13540/student/html/simulation2_3.html
3.6 Zadania
Zadanie 3.1 Dane są następujące obserwacje:
\[x_1 = 2,\; x_2 = 4,\; x_3 = 1,\; x_4 = 3,\; x_5 = 5,\; x_6 = 2,\; x_7 = 4\]
Oblicz:
\(\displaystyle \sum_{i=1}^{7} x_i\)
\(\displaystyle\frac{1}{7}\sum_{i=1}^7 x_i\)
\(\displaystyle \sum_{i=1}^{7} x_i^2\)
\(\displaystyle \sum_{i=1}^{5} x_i\)
\(\displaystyle \sum_{i=1}^{7} (x_i - \overline{x}) \quad \text{gdzie } \quad \overline{x} = \frac{1}{7}\sum_{i=1}^7 x_i\)
\(\displaystyle \frac{1}{7}\sum_{i=1}^7 x_i+2\)
\(\displaystyle \prod_{i=1}^{7} x_i\)
\(\displaystyle \sum_{i=1}^{7} i\)
\(\displaystyle \prod_{i=1}^{7} i\)
Zadanie 3.2
Przez godzinę jechaliśmy z prędkością 60 km/h, przez kolejną godzinę jechaliśmy 120 km/h. Z jaką średnią prędkością jechaliśmy?
Na odcinku 100 km jechaliśmy z prędkością 60 km/h, na odcinku 100 km jechaliśmy z prędkością 120 km/h. Z jaką średnią prędkością jechaliśmy?
Przez 60% czasu (np. 3 z 5 godzin) jechaliśmy z prędkością 60 km/h, przez 40% czasu (np. 2 z 5 godzin) jechaliśmy z prędkością 120 km/h. Z jaką średnią prędkością jechaliśmy?
Przez 60% drogi (np. 300 km) jechaliśmy z prędkością 60 km/h, a przez 40% drogi (np. 200 km) jechaliśmy z prędkością 120 km/h. Z jaką średnią prędkością jechaliśmy?
Zadanie 3.3 Na podstawie danych o zamówieniach ze sklepu internetowego (orders.csv) oblicz i zinterpretuj medianę kwoty zamówienia, pierwszy kwartyl, trzeci kwartyl, dziesiąty i dziewięćdziesiąty centyl. Ile wynosi IQR?
Zadanie 3.4 Na podstawie danych z radaru (SpeedRadarData.csv) oblicz i zinterpretuj medianę, dolny i górny kwartyl dla
jednośladów,
samochodów osobowych.
Z czego mogą wynikać różnice?