12.1 Correlação

Correlação é uma medida estatística que indica o grau de relação entre duas variáveis. Quando duas variáveis estão correlacionadas, significa que mudanças em uma tendem a estar associadas a mudanças na outra. Por exemplo, se ao aumentar o tempo de estudo as notas de um aluno também aumentam, dizemos que há uma correlação positiva. Já se o aumento de uma variável estiver relacionado à diminuição da outra, como o número de horas de sono e o nível de cansaço, temos uma correlação negativa.

É importante lembrar que correlação não implica causalidade — ou seja, só porque duas coisas estão relacionadas, não significa que uma causa a outra.

Vamos criar uma nova tabela selecionando algumas variáveis quantitativas do banco dados.

dadosquant=dados%>%select(idade,tempo_emprestimo,tempo_empresa)

A função cor.test() no R é usada para testar se há uma correlação estatisticamente significativa entre duas variáveis numéricas. Ela realiza um teste de correlação de Pearson, Spearman ou Kendall, dependendo do método especificado. (Caso o método não seja especificado o padrão utilizado é o método de Pearson)

cor.test(dadosquant$idade, dadosquant$tempo_emprestimo, method="pearson")

## 
##  Pearson's product-moment correlation
## 
## data:  dadosquant$idade and dadosquant$tempo_emprestimo
## t = -3.4573, df = 4451, p-value = 0.0005506
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.08100211 -0.02241401
## sample estimates:
##         cor 
## -0.05175259

Você verá:

t: estatística do teste t df: graus de liberdade p-value: valor-p para testar se a correlação é significativamente diferente de zero 95% CI: intervalo de confiança da correlação cor: o valor da correlação (coeficiente de Pearson)

Podemos também criar uma matriz de correlação com todas a variáveis através da função cor()

cor(dadosquant)

##                        idade tempo_emprestimo tempo_empresa
## idade             1.00000000      -0.05175259    0.50604515
## tempo_emprestimo -0.05175259       1.00000000   -0.02168664
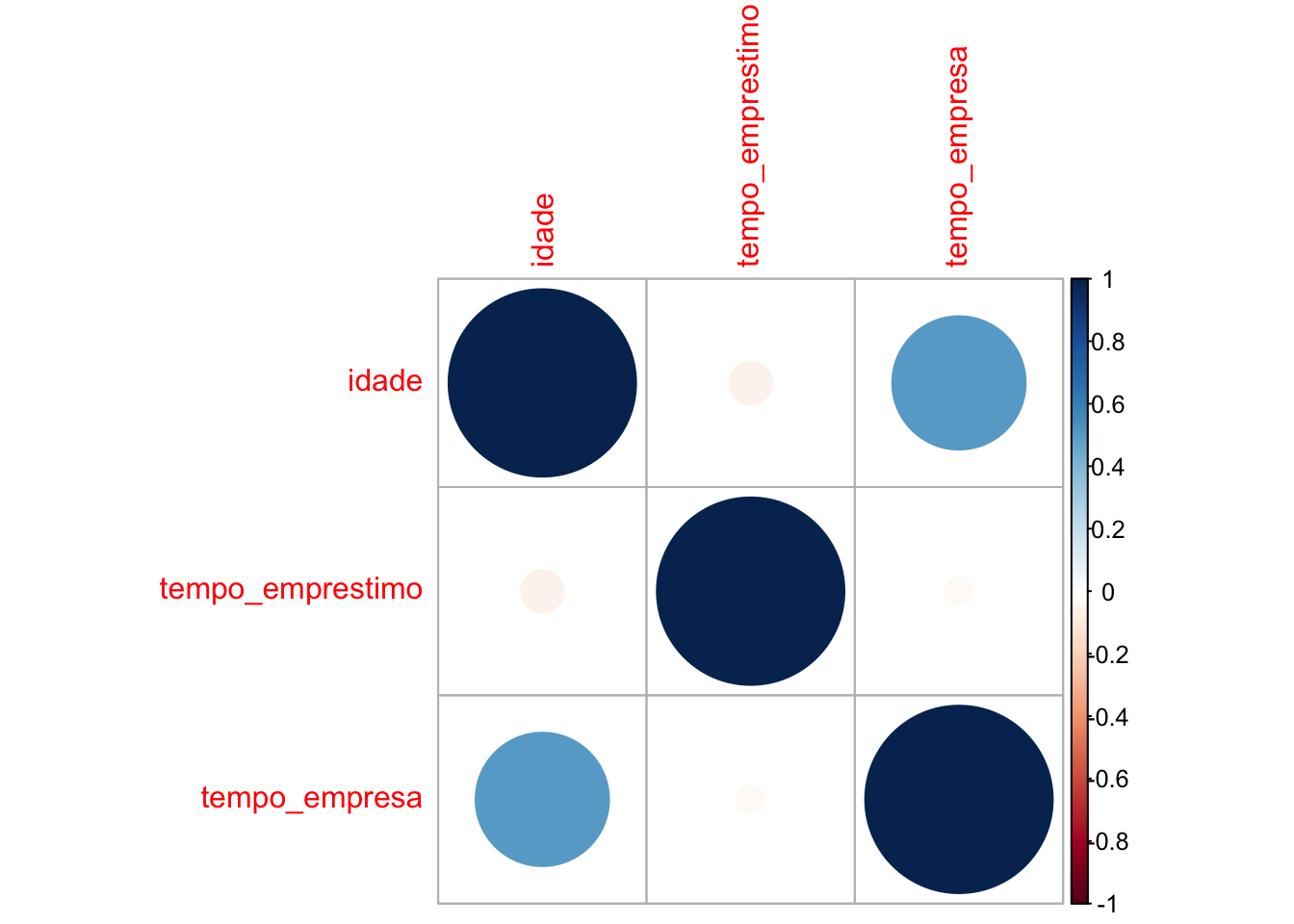
## tempo_empresa     0.50604515      -0.02168664    1.00000000

Podemos também criar uma matriz de correlação visual com o pacote corrplot. Para isso instalamos e carregamos o pacote:

library(corrplot)

## corrplot 0.92 loaded

Em seguida precisamos salvar a matriz de correlação um novo objeto

matriz=cor(dadosquant)

Por fim, utilizamos a função corrplot()

corrplot(matriz, method="circle")