6 Machine Learning - Regressão
A Regressão é uma área do Machine Learning que é bastante utilizada quando de deseja prevê valores a partir de uma ou mais variáveis explicativas, ou seja, quando se deseja prevê a resposta através de um modelo de regressão.
6.1 Banco de dados
O banco de dados utilizado são conjuntos de dados históricos de transações ocorridas entre os anos de 2012 a 2013 no mercado de avaliação de imóveis de Xindian District., New Taipei City, Taiwan. As variáveis explicativas do banco de dados são:
house_age: Idade da casa (unidade: anos);
distance_station: Distância até a estação mais próxima (unidade: metro);
number_stores: O número de lojas de conveniência no círculo vivo a pé (inteiro);
latitude: Coordenada geográfica (unidade: grau);
longitude: Coordenada geográfica (unidade: grau).
A variável resposta que queremos prevê é:
Price_house: Preço da casa por unidade de área (1:10000 em dólar taiwanês/Ping, onde Ping = 3,3 metros quadrados)
Os dados podem ser encontrados acessando:
6.2 Análise exploratória
Antes da aplicação dos algoritmos de regressão, é necessário realizar uma análise inicial nos dados para verificar como se comportam.
6.2.1 Preparação dos dados
Comece carregando o banco de dados, onde header = TRUE significa que a primeira linha do arquivo deve ser interpretada como os nomes das colunas e sep = indica o tipo de separador de colunas e dec = refere-se ao tipo de separador decimal.
dados = read.csv("Real_estate_valuation.csv", header = T, sep = ";", dec = ",")6.2.2 Pacotes utilizados
Antes carrega-se os pacotes que serão utilizados ao longo da análise, são eles, tidymodels para uso dos algoritmos de Machine Learning, GGally para verificar a correlação e dispersão, knitr e kableExtra para geração de tabelas.
library(tidymodels)
library(GGally)
library(knitr)
library(kableExtra)Retirando as variáveis que não são de interesse na análise, pois não possuem nenhuma influência em relação a variável resposta.
dados$id = NULL
dados$date = NULLO resultado do código abaixo mostra que não existe nenhuma observação faltante no conjunto de dados.
sum(!complete.cases(dados))## [1] 0Usando a função glimpse() pode-se visualizar os tipos das variáveis.
glimpse(dados)## Rows: 414
## Columns: 6
## $ house_age <dbl> 32.0, 19.5, 13.3, 13.3, 5.0, 7.1, 34.5, 20.3, 31.7, 1…
## $ distance_station <dbl> 84.87882, 306.59470, 561.98450, 561.98450, 390.56840,…
## $ number_stores <int> 10, 9, 5, 5, 5, 3, 7, 6, 1, 3, 1, 9, 5, 4, 4, 2, 6, 1…
## $ latitude <dbl> 24.98298, 24.98034, 24.98746, 24.98746, 24.97937, 24.…
## $ longitude <dbl> 121.5402, 121.5395, 121.5439, 121.5439, 121.5425, 121…
## $ Price_house <dbl> 37.9, 42.2, 47.3, 54.8, 43.1, 32.1, 40.3, 46.7, 18.8,…Observa-se que todas as variáveis são inteiras e estão em classe de medida diferentes. Utlizando o pacote GGally pode-se verificar pela Figura 6.1 o comportamento das variáveis.
ggpairs(dados)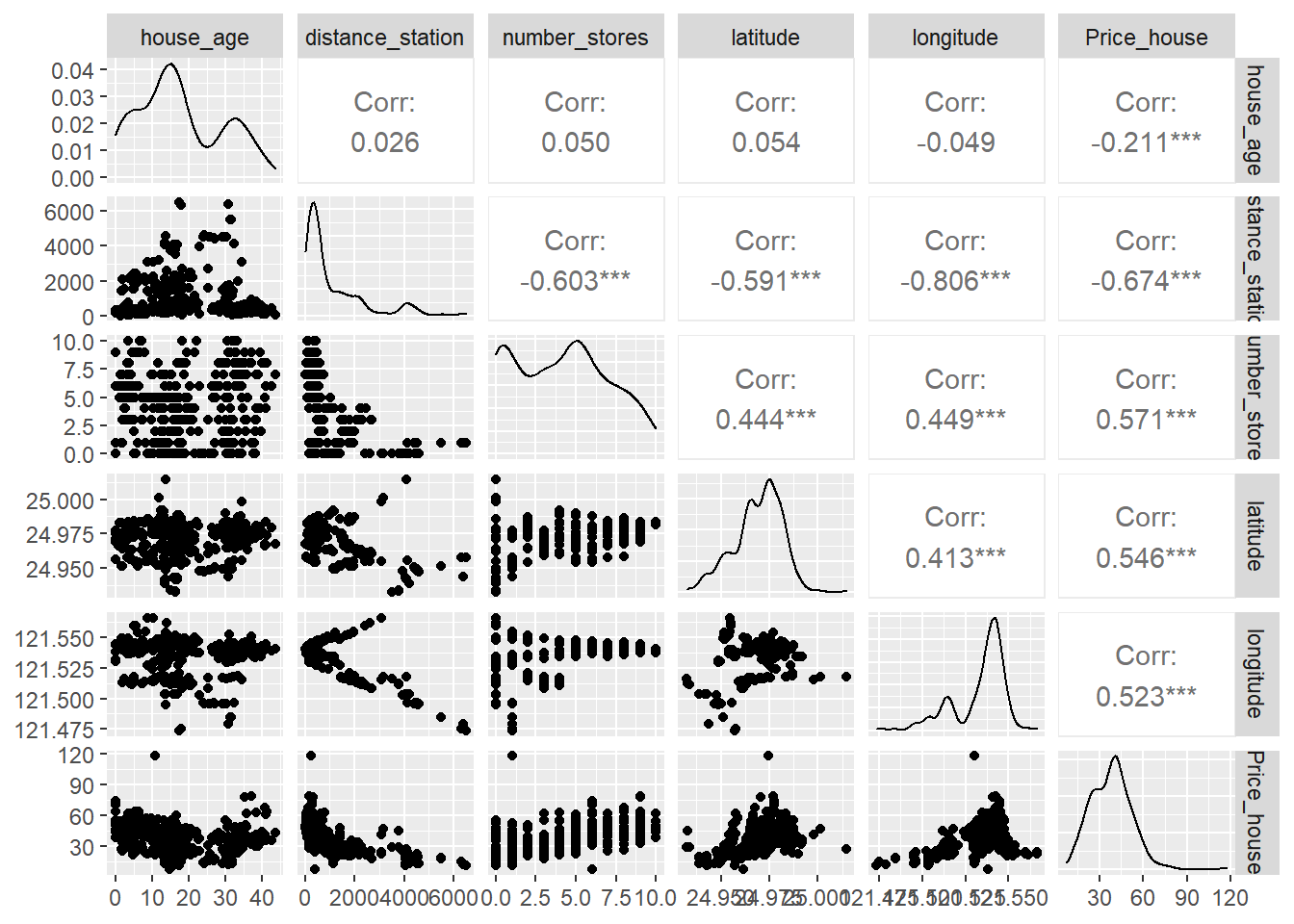
Figure 6.1: Visualização gráfica do comportamento das variáveis explicativas.
Nenhuma variável apresenta correlação superior a 0.90, e também não possuem um comportamento simétrico. A seguir obtém-se algumas estatísticas descritivas.
summary(dados)## house_age distance_station number_stores latitude
## Min. : 0.000 Min. : 23.38 Min. : 0.000 Min. :24.93
## 1st Qu.: 9.025 1st Qu.: 289.32 1st Qu.: 1.000 1st Qu.:24.96
## Median :16.100 Median : 492.23 Median : 4.000 Median :24.97
## Mean :17.713 Mean :1083.89 Mean : 4.094 Mean :24.97
## 3rd Qu.:28.150 3rd Qu.:1454.28 3rd Qu.: 6.000 3rd Qu.:24.98
## Max. :43.800 Max. :6488.02 Max. :10.000 Max. :25.01
## longitude Price_house
## Min. :121.5 Min. : 7.60
## 1st Qu.:121.5 1st Qu.: 27.70
## Median :121.5 Median : 38.45
## Mean :121.5 Mean : 37.98
## 3rd Qu.:121.5 3rd Qu.: 46.60
## Max. :121.6 Max. :117.50Obtém-se o bloxplot da variável resposta Price_house para verificar a existência de possíveis valores discrepantes.
boxplot(dados$Price_house)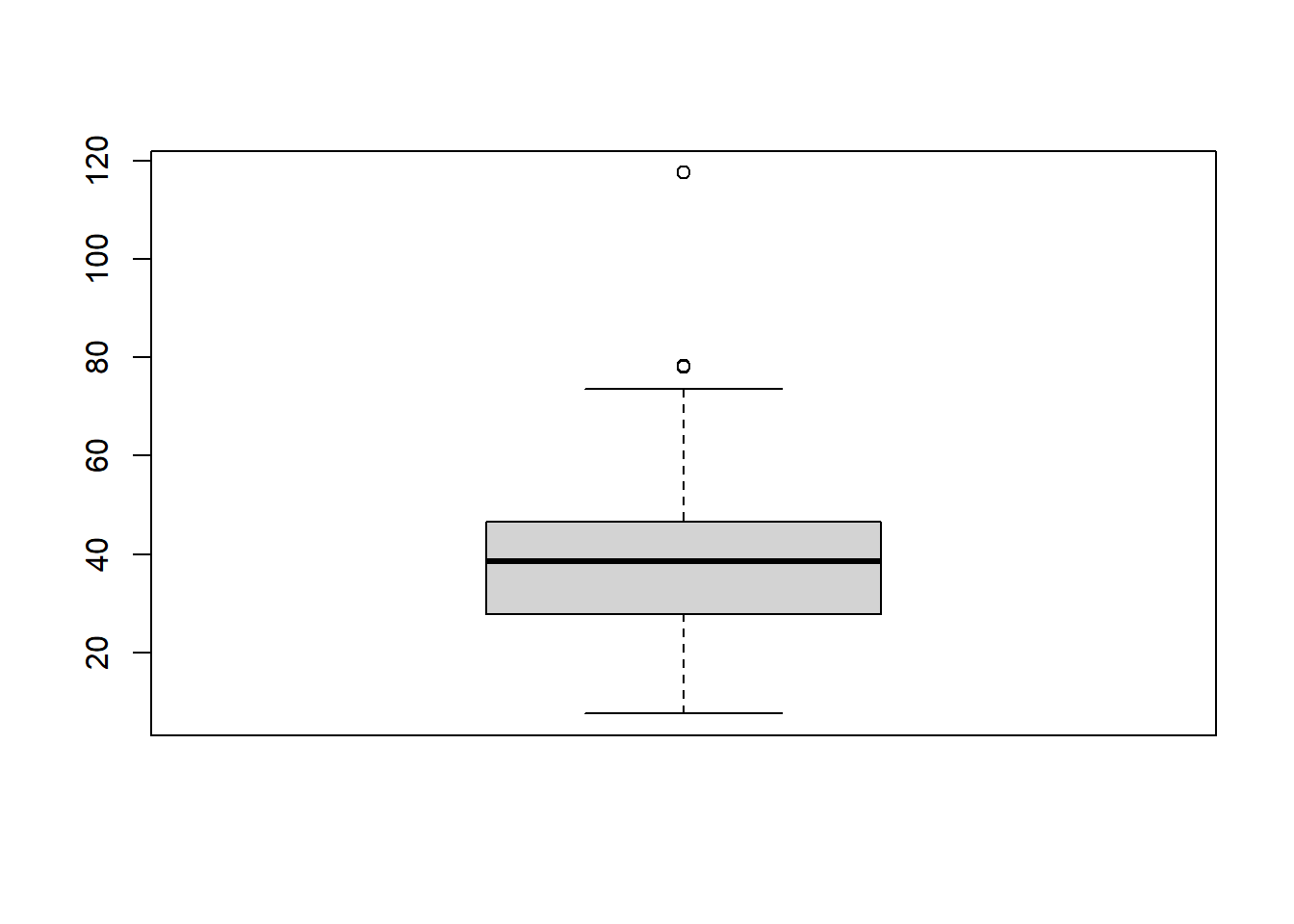
É observado alguns pontos discrepantes, a seguir é realizado uma filtragem para avaliar quais são essas observações.
dados %>%
filter(Price_house > 75.0)## id house_age distance_station number_stores Price_house
## 1 221 37.2 186.5101 9 78.3
## 2 271 10.8 252.5822 1 117.5
## 3 313 35.4 318.5292 9 78.0Observa-se que são três observações que podem representar pontos outliers, considerando as informações obtidas na Figura 6.1, as variáveis distance_station e number_stores são as que possuem maior correlação com a variável resposta, nesta ordem. Valores discrepantes podem resultar em erros altos, principalmente quando se trata de predições.
Observa-se que a casa que possui o valor de NT$ 117.5 (em dezenas de milhar) possui apenas uma loja próxima e não possui a menor distância até o metrô mais próximo. A seguir é feito uma filtragem para avaliar os valores de outras casas que preenchem o mesmo requisito da casa em questão.
dados %>%
filter(distance_station < 253, number_stores < 2)## id house_age distance_station number_stores Price_house
## 1 102 12.7 170.1289 1 32.9
## 2 124 0.0 185.4296 0 45.5
## 3 147 0.0 185.4296 0 52.2
## 4 165 0.0 185.4296 0 55.2
## 5 271 10.8 252.5822 1 117.5
## 6 274 13.2 170.1289 1 29.3
## 7 307 14.4 169.9803 1 50.2
## 8 323 12.9 187.4823 1 33.1
## 9 346 0.0 185.4296 0 37.9
## 10 357 10.3 211.4473 1 45.3
## 11 387 0.0 185.4296 0 55.3
## 12 400 12.7 170.1289 1 37.3
## 13 403 12.7 187.4823 1 28.5Observa-se casas com distância menor até a estação mais próxima se comparado com a casa de id 271 e com valores em dólar taiwanês bem menores. Na sequência é verificado as outras duas observações.
dados %>%
filter(distance_station < 319, number_stores >= 9)## id house_age distance_station number_stores Price_house
## 1 1 32.0 84.87882 10 37.9
## 2 2 19.5 306.59470 9 42.2
## 3 12 6.3 90.45606 9 58.1
## 4 71 6.6 90.45606 9 59.0
## 5 97 6.4 90.45606 9 59.5
## 6 100 6.4 90.45606 9 62.2
## 7 173 6.6 90.45606 9 58.1
## 8 178 33.0 181.07660 9 42.0
## 9 214 6.2 90.45606 9 58.0
## 10 221 37.2 186.51010 9 78.3
## 11 253 5.9 90.45606 9 52.7
## 12 287 5.9 90.45606 9 56.3
## 13 300 33.2 121.72620 10 46.1
## 14 313 35.4 318.52920 9 78.0
## 15 339 31.5 258.18600 9 36.3
## 16 343 5.7 90.45606 9 53.5
## 17 361 32.9 87.30222 10 47.1
## 18 364 32.3 109.94550 10 48.0
## 19 382 8.0 132.54690 9 47.3
## 20 386 18.3 82.88643 10 46.6
## 21 404 30.9 161.94200 9 39.7
## 22 411 5.6 90.45606 9 50.0
## 23 414 6.5 90.45606 9 63.9Os demais imóveis localizados apresentam valores menores e a maioria com distância até o metrô mais próximo inferior a 186 metros. O imóvel com maior valor em dólar taiwanês com exceção das observações 221 e 313 é aquele com id 414 porém a distância até o metrô mais próximo é de apenas 95 metros e a idade da casa é inferior a 7 anos.
As observações 221, 271 e 313 podem não ser resultantes de erro de coleta, mas para casos que envolve predições podem gerar altos erros nos modelos, devido isso opta-se pela retirada das mesmas do conjunto de dados.
6.3 Regressão Linear
A regressão linear é usada para investigar e modelar a relação entre duas ou mais variáveis, de modo que uma variável pode ser predita a partir de outra ou outras variáveis. O modelo de regressão linear é dado por:
\[Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \dots + \beta_kX_k + \epsilon\]
Onde,
\(Y\): é a variável dependente (ou explicada).
\(X_1, X_1, ..., X_k\): são as variáveis independentes (ou explicativas).
\(\beta_0, \beta_1, ..., \beta_k\): parâmetros da regressão ou coeficientes angulares.
\(\epsilon\): é o termo que representa o erro aleatório.
O caso mais simples de regressão é quando temos duas variáveis e a relação entre elas pode ser representada por uma linha reta, para o caso da Regressão Linear Simples, conforme Figura 6.2.
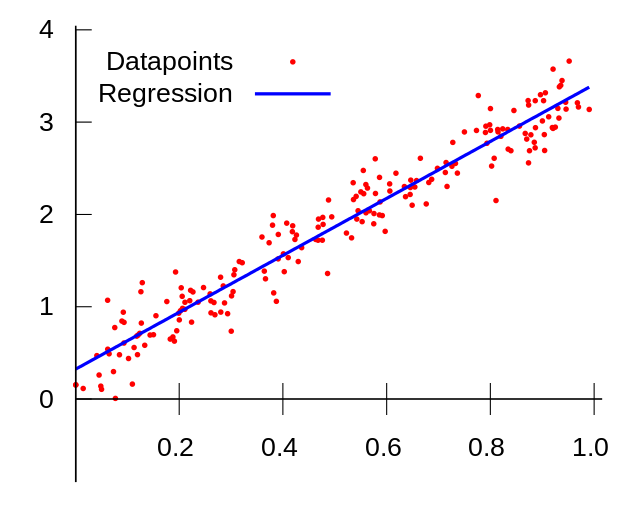
Figure 6.2: Representação de uma reta ajustada em regressão linear.
Fonte: https://pt.wikipedia.org/
O resultado da regressão linear é sempre um número. Em machine learning é comum utilizar a reta de regressão para avaliar o desempenho de um modelo, onde avaliar-se os valores reais e os valores preditos atráves de uma reta de regressão, porém nenhuma decisão deve ser tomada com base apenas na visualização gráfica de um modelo.
6.3.1 Divisão dos dados
set.seed(1626)
divisao <- initial_split(dados)
divisao## <Analysis/Assess/Total>
## <308/103/411>O conjunto de dados é dividido em aproximadamente 75% dos dados para treinamento e 25% para teste, abaixo é carregado os dados para treino e teste respectivamente. Nessa situação como deseja-se prever o valor médio das casas, não é necessário usar nenhum tipo de estratificação.
data_treino <- training(divisao)
data_teste <- testing(divisao)Os dados de treinamento serão usados para ajustar os modelos e seus parâmetros, e os dados de teste serão usados para avaliar o desempenho do modelo final.
6.3.2 Pré - processamento
pre_recipe <- recipe(Price_house ~ ., data = data_treino) %>%
step_scale(all_predictors()) Primeiramente a função recipe() recebe a variável resposta Price_house em relação a todas as demais variáveis (.) e atribui-se os dados de treinamento. A função step_scale() é utilizada para padronizar as variáveis preditoras e deixá-las em um mesma escala de medida.
Observe que a receita foi salva em um objeto chamado pre_recipe que será utilizado para todos os modelos de regressão que serão ajustado a partir deste conjunto de dados.
6.3.3 Validação cruzada
Na validação cruzada o vfold_cv() já divide por padrão em 4 partes v = 4.
set.seed(1626)
val_set <- vfold_cv(data_treino, v = 4)6.3.4 Definição do modelo
Define-se o modelo que será utilizado, neste caso é o modelo de Regressão Linear linear_reg() que recebe os argumentos penalty que é o número não negativo que representa a quantidade total de regularização e mixture um número entre zero e um que é a proporção de regularização no modelo. Para ambos os parâmetros atribui-se a função tune() que significa que os valores serão ajustados pelo pipeline. Em outras palavras, serão ajustados vários modelos e posteriormente escolhe-se aquele que obtiver melhores resultados.
reg_model <- linear_reg(penalty = tune(),
mixture = tune()) %>%
set_engine('glmnet')A função set_engine() define o pacote que será utilizado para o ajuste, neste caso não é preciso definir qual o tipo de modelo, visto que a Regressão Linear é apenas um modelo de Regressão. Após a definição do modelo é criado o fluxo de trabalho workflow().
reg_workflow <- workflow() %>%
add_model(reg_model) %>%
add_recipe(pre_recipe)O modelo add_model() e o pré-procesamento add_recipe() são colocados dentro de um workflow() e salvo em um objeto chamado reg_workflow.
6.3.5 Treinamento
Nessa etapa é realizado o treinamento do modelo para o algoritmo Regressão Linear.
reg_trained <- reg_workflow %>%
tune_grid(
val_set,
grid = 10,
control = control_grid(save_pred = TRUE),
metrics = metric_set(rmse)
)Utilizou-se como métrica para avaliar o desempenho dos modelos o RMSE que é a Raiz do Erro Quadrático Médio, usada para expressar a acurácia do modelo. Quanto maior for o valor do RMSE, pior o desempenho do modelo.
reg_trained %>% show_best("rmse")## # A tibble: 5 × 8
## penalty mixture .metric .estimator mean n std_err .config
## <dbl> <dbl> <chr> <chr> <dbl> <int> <dbl> <chr>
## 1 2.82e- 1 0.0733 rmse standard 7.84 4 0.534 Preprocessor1_Model01
## 2 3.15e- 6 0.238 rmse standard 7.84 4 0.532 Preprocessor1_Model02
## 3 4.13e-10 0.243 rmse standard 7.84 4 0.532 Preprocessor1_Model03
## 4 1.87e- 7 0.387 rmse standard 7.84 4 0.531 Preprocessor1_Model04
## 5 3.24e- 9 0.518 rmse standard 7.84 4 0.530 Preprocessor1_Model05Observa-se os modelos gerado em função do valor do RMSE, do menor para o maior. Para selecionar o melhor modelo, usa-se a funçãoselect_best() defindo a métrica que será utilizada.
6.3.6 Seleção do melhor modelo
reg_best_tune <- select_best(reg_trained, 'rmse')
final_reg_model <- reg_model %>%
finalize_model(reg_best_tune)
reg_best_tune ## # A tibble: 1 × 3
## penalty mixture .config
## <dbl> <dbl> <chr>
## 1 0.282 0.0733 Preprocessor1_Model01O melhor modelo foi o Modelo 1 com RMSE de 7.84, observe que o modelo foi selecionado e aplicado no objeto final_reg_model que será utilizado a seguir para aplicação nos dados de teste.
6.3.7 Aplicando os dados de teste ao modelo
Na etapa final é criado o novo fluxo de trabalho onde é submetido os dados de teste ao modelo escolhido após a etapa de treinamento. É adicionado em add_recipe() o pré-processamento dos dados criado na etapa inicial, em add_model() é adicionado o modelo final. A função last_fit() indica que é último ajuste a ser realizado.
previsoes <- workflow() %>%
add_recipe(pre_recipe) %>%
add_model(final_reg_model) %>%
last_fit(divisao)Usando collect_predictions() visualizamos as previsões salva no objeto previsoes.
previsoes %>% collect_predictions() ## # A tibble: 103 × 5
## id .pred .row Price_house .config
## <chr> <dbl> <int> <dbl> <chr>
## 1 train/test split 48.5 2 42.2 Preprocessor1_Model1
## 2 train/test split 32.9 6 32.1 Preprocessor1_Model1
## 3 train/test split 44.9 8 46.7 Preprocessor1_Model1
## 4 train/test split 7.20 9 18.8 Preprocessor1_Model1
## 5 train/test split 32.2 10 22.1 Preprocessor1_Model1
## 6 train/test split 41.2 13 39.3 Preprocessor1_Model1
## 7 train/test split 35.2 16 50.5 Preprocessor1_Model1
## 8 train/test split 44.9 19 42.3 Preprocessor1_Model1
## 9 train/test split 30.2 23 24.6 Preprocessor1_Model1
## 10 train/test split 48.0 24 47.9 Preprocessor1_Model1
## # … with 93 more rowsPode-se visualizar os resultados de previsões em .pred e comparar com os valores originais (Price_house) da base de dados de teste. A Figura 6.3 retorna a reta ajustada dos valores preditos vs valores reais.
previsoes %>%
collect_predictions() %>%
select(.row, Price_house, .pred) %>%
ggplot() +
aes(x = Price_house, y = .pred) +
geom_point() +
geom_abline() 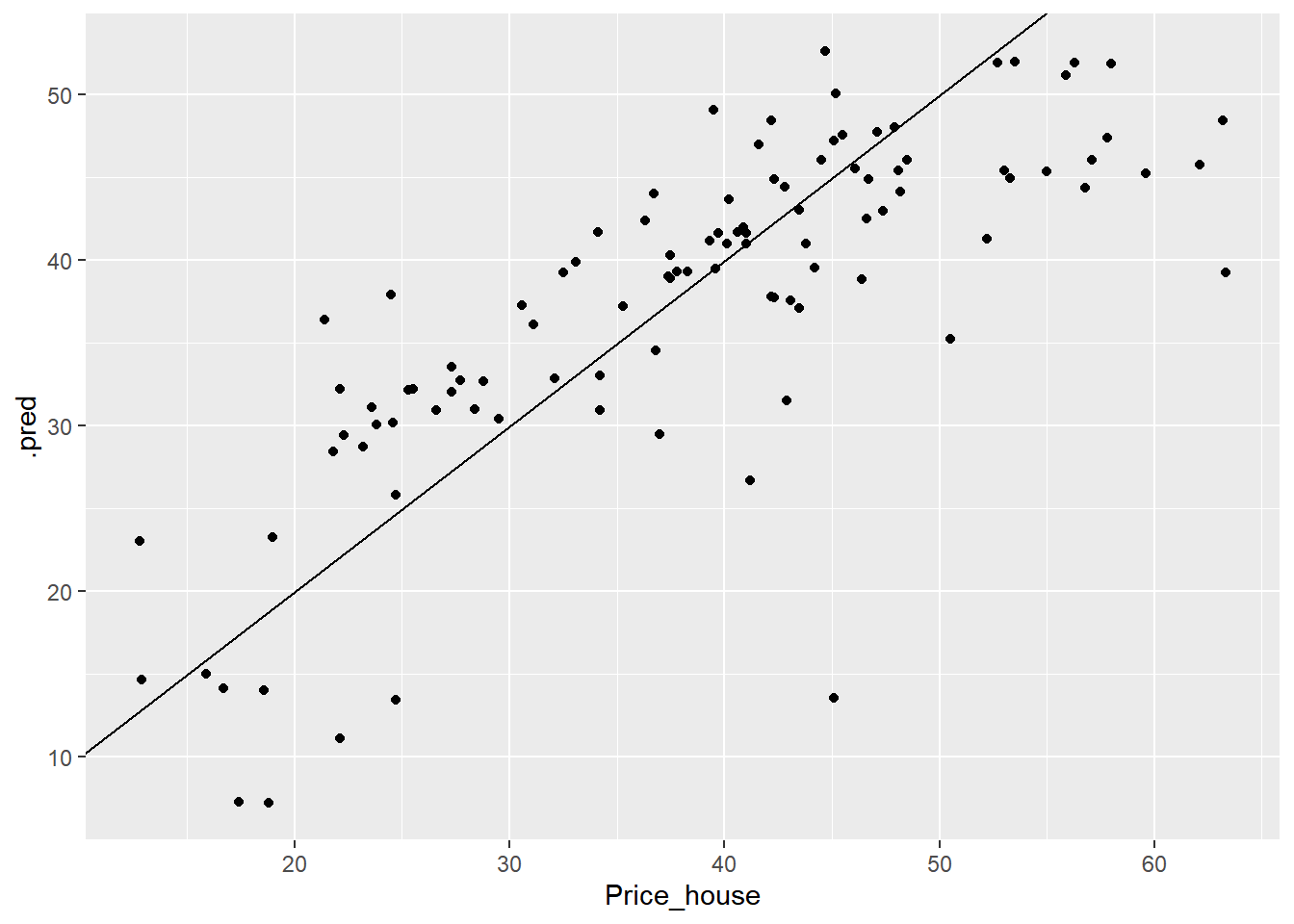
Figure 6.3: Valores preditos vs Valores observados para Regressão Linear.
O modelo de Regressão Linear aplicado aos dados de teste, apresenta um comportamento em torno de reta linear com algumas observações dispersas. A seguir obtem-se o RMSE dos dados de teste.
previsoes %>% collect_metrics("rmse")## # A tibble: 2 × 4
## .metric .estimator .estimate .config
## <chr> <chr> <dbl> <chr>
## 1 rmse standard 7.77 Preprocessor1_Model1
## 2 rsq standard 0.603 Preprocessor1_Model1O RMSE obtido para os dados de teste é de 7.77, que é um pouco menor comparado com o RMSE obtido nos dados de treino.
Outros modelos foram aplicados ao dados de previsão de valores de imóveis, conforme segue.
6.4 Regressão com Random Forest
Para entender sobre o funcionamento do algoritmo Random Forest consulte a seção 5.4.
É importante entender que na regressão o algoritmo de Random Forest usa a média para predição de valores e na classificação usa os votos da maioria para da a resposta final.
6.4.1 Definição do modelo
Define-se o modelo que será utilizado, nesse caso é o algoritmo Random Forest rand_forest() que recebe os argumentos mtry que determina o número de preditores que serão amostrados ateatoriamente em cada divisão, trees que determina o número de árvores contidas no conjunto e min_n um número inteiro para o número mínimo de pontos de dados em um nó que são necessários para que o nó seja dividido ainda mais. Para os argumentos mtry e min_n atribui-se a função tune() que significa que os valores serão ajustados pelo pipeline, para trees foi atribuido o total de 1000 árvores.
rf_model <- rand_forest(mtry = tune(), min_n = tune(),
trees = 1000) %>%
set_engine('ranger') %>%
set_mode('regression')A função set_engine() define o pacote que será utilizado para o ajuste, e set_mode() define o modelo. Dessa vez estamos usando um modelo de regressão.
Após a definição do modelo é criado o fluxo de trabalho workflow().
rf_workflow <- workflow() %>%
add_model(rf_model) %>%
add_recipe(pre_recipe)O modelo add_model() e o pré-procesamento add_recipe() são colocados dentro de um workflow() e salvo em um objeto chamado rf_workflow.
6.4.2 Treinamento
Nessa etapa é realizado o treinamento do modelo para o algoritmo de Random Forest.
rf_trained <- rf_workflow %>%
tune_grid(
val_set,
grid = 10,
control = control_grid(save_pred = TRUE),
metrics = metric_set(rmse)
)Obtendo os modelos gerados a partir dos dados de treinamento.
rf_trained %>% show_best("rmse")## # A tibble: 5 × 8
## mtry min_n .metric .estimator mean n std_err .config
## <int> <int> <chr> <chr> <dbl> <int> <dbl> <chr>
## 1 3 6 rmse standard 5.93 4 0.526 Preprocessor1_Model03
## 2 4 8 rmse standard 5.93 4 0.556 Preprocessor1_Model07
## 3 4 11 rmse standard 5.95 4 0.566 Preprocessor1_Model09
## 4 3 15 rmse standard 5.97 4 0.546 Preprocessor1_Model05
## 5 3 19 rmse standard 6.03 4 0.550 Preprocessor1_Model06Para interpretação dos resultados temos que, quanto menor for o RMSE melhor é o modelo. Para selecionar o melhor modelo usamos select_best().
6.4.3 Seleção do melhor modelo
rf_best_tune <- select_best(rf_trained, 'rmse')
final_rf_model <- rf_model %>%
finalize_model(rf_best_tune)
rf_best_tune ## # A tibble: 1 × 3
## mtry min_n .config
## <int> <int> <chr>
## 1 3 6 Preprocessor1_Model03O Modelo 3 foi o melhor, com RMSE de 5.93.
6.4.4 Aplicando os dados de teste ao modelo
Na etapa final é criado o novo fluxo de trabalho onde é submetido os dados de teste ao modelo escolhido após o treinamento do modelo. É adicionado em add_recipe() o pré-processamento dos dados criado no início, em add_model() é adicionado o modelo final. A função last_fit() indica que é último ajuste a ser realizado.
previsoes <- workflow() %>%
add_recipe(pre_recipe) %>%
add_model(final_rf_model) %>%
last_fit(divisao) Usando collect_predictions() visualiza-se os resultados salvo no objeto previsoes.
previsoes %>% collect_predictions()## # A tibble: 103 × 5
## id .pred .row Price_house .config
## <chr> <dbl> <int> <dbl> <chr>
## 1 train/test split 42.0 2 42.2 Preprocessor1_Model1
## 2 train/test split 27.8 6 32.1 Preprocessor1_Model1
## 3 train/test split 46.1 8 46.7 Preprocessor1_Model1
## 4 train/test split 15.9 9 18.8 Preprocessor1_Model1
## 5 train/test split 23.2 10 22.1 Preprocessor1_Model1
## 6 train/test split 40.6 13 39.3 Preprocessor1_Model1
## 7 train/test split 39.0 16 50.5 Preprocessor1_Model1
## 8 train/test split 40.8 19 42.3 Preprocessor1_Model1
## 9 train/test split 27.3 23 24.6 Preprocessor1_Model1
## 10 train/test split 54.0 24 47.9 Preprocessor1_Model1
## # … with 93 more rowsPode-se visualizar os resultados das previsões em .pred e comparar com os valores originais (Price_house) da base de dados de teste. A Figura 6.4 retorna a reta ajustada dos valores preditos vs valores reais.
previsoes %>%
collect_predictions() %>%
select(.row, Price_house, .pred) %>%
ggplot() +
aes(x = Price_house, y = .pred) +
geom_point() +
geom_abline() 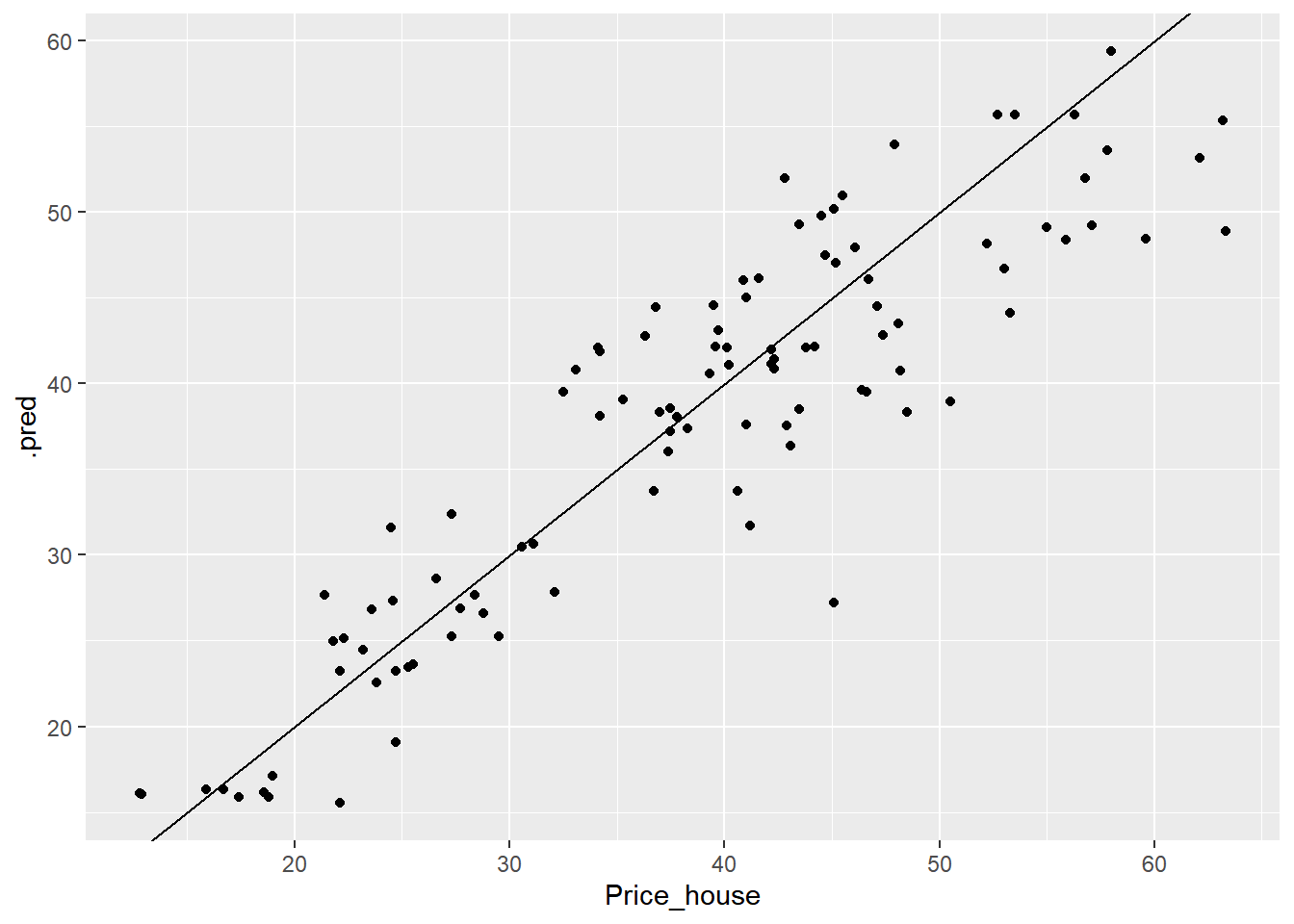
Figure 6.4: Valores preditos vs Valores observados com Random Forest.
Obtendo o RMSE dos dados de teste.
previsoes %>% collect_metrics("rmse")## # A tibble: 2 × 4
## .metric .estimator .estimate .config
## <chr> <chr> <dbl> <chr>
## 1 rmse standard 5.32 Preprocessor1_Model1
## 2 rsq standard 0.813 Preprocessor1_Model1O modelo de Random Forest aplicados aos dados de teste obteve o RMSE de 5.32, observa-se que o modelo generalizou melhor no dados de teste. Comparando esse resultado com a Regressão Linear e observando o RMSE para o melhor modelo de cada algoritmo, temos que o desempenho foi melhor para o algoritmo Random Forest.
A seguir ajusta-se o algoritmo de regressão com XGBoost para avaliar o seu desempenho.
6.5 Regressão com XGBoost
O eXtreme Gradient Boosting (XGBoost) é um algoritmo de aprendizado de máquina baseado em árvore de decisão e que utiliza uma estrutura de Gradient boosting. O Gradient boosting produz modelos preditivos melhores a partir de modelo de preditores fracos.
O XGBoost é um algoritmo que combina técnicas de otimização do uso de software e hardware e produz resultados superiores usando menos recursos de computação, se comparado com os demais algoritmos baseados em árvores de decisão.
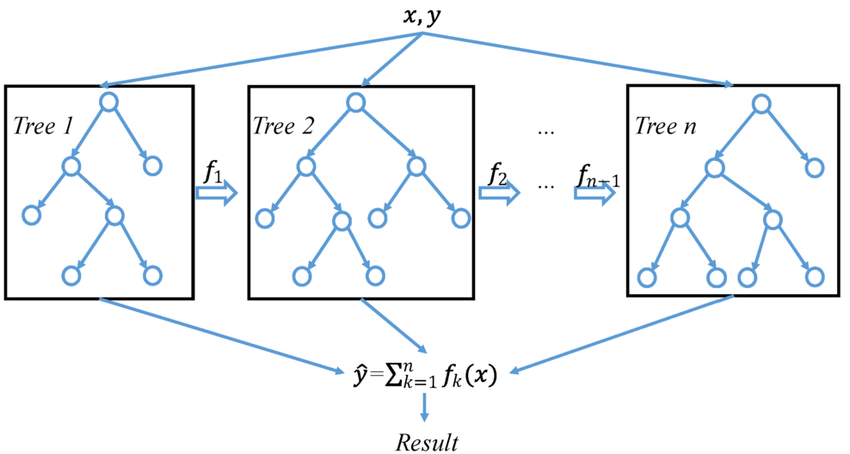
Figure 6.5: Exemplo de uma árvore usando eXtreme Gradient Boosting.
Fonte: https://www.lokshop.cf/
Conforme pode ser observado na Figura 6.5, cada novo modelo adicionado é uma árvore de decisão, os modelos são construidos em sequência e cada novo modelo tenta corrigir a deficiência do modelo anterior.
Além de utilizar menos recursos computacionais, sendo mais rápido e mais robusto que os algoritmos baseado em gradiente boosting, o XGBoost utiliza alguns recursos para regularição do overfitting.
6.5.1 Definição do modelo
Define-se o modelo que será utilizado, nesse caso é o algoritmo eXtreme Gradient Boosting (XGBoost) boost_tree() que recebe os hiperparâmetrostree_depth que é a profundidade da árvore, learn_rate a taxa de aprendizagem, loss_reduction o tamanho mínimo do nó, min_n um número inteiro para o número mínimo de pontos de dados em um nó, sample_size a proporção de observações amostradas e trees que determina o número de árvores contidas no conjunto. Para todos os argumentos atribui-se a função tune() que significa que os valores serão ajustados pelo pipeline.
library(xgboost)
xgb_model <- boost_tree(tree_depth = tune(), learn_rate = tune(),
loss_reduction = tune(), min_n = tune(),
sample_size = tune(), trees = tune()) %>%
set_engine('xgboost') %>%
set_mode('regression')A função set_engine() para definir o pacote que será utilizado e set_mode() para definir o modelo de regressão.
Após a definição do modelo é criado o fluxo de trabalho workflow().
xgb_workflow <- workflow() %>%
add_model(xgb_model) %>%
add_recipe(pre_recipe)O modelo add_model() e o pré-procesamento add_recipe() são colocados dentro de um workflow() e salvo em um objeto chamado xgb_workflow.
6.5.2 Treinamento
Nessa etapa é realizado o treinamento do modelo para o algoritmo XGBoost.
xgb_trained <- xgb_workflow %>%
tune_grid(
val_set,
grid = 10,
control = control_grid(save_pred = TRUE),
metrics = metric_set(rmse)
)Obtendo os modelos gerados a partir dos dados de treinamento.
mod = xgb_trained %>% show_best("rmse")
mod## # A tibble: 5 × 12
## trees min_n tree_depth learn_rate loss_reduction sample_size .metric
## <int> <int> <int> <dbl> <dbl> <dbl> <chr>
## 1 920 10 7 0.0309 3.60e- 5 0.726 rmse
## 2 329 27 2 0.0443 8.03e- 3 0.861 rmse
## 3 1788 14 6 0.0772 5.82e+ 0 0.480 rmse
## 4 1427 24 4 0.105 6.23e-10 0.933 rmse
## 5 779 36 8 0.00633 3.16e- 7 0.624 rmse
## # … with 5 more variables: .estimator <chr>, mean <dbl>, n <int>,
## # std_err <dbl>, .config <chr>Como o algoritmo XGBoost possui muitos hiperparâmetros utilizamos a função select() do pacote dplyr para selecionar alguns dos hiperparâmetros de interesse.
select(mod, trees, min_n, tree_depth, .metric, mean, std_err, .config)## # A tibble: 5 × 7
## trees min_n tree_depth .metric mean std_err .config
## <int> <int> <int> <chr> <dbl> <dbl> <chr>
## 1 920 10 7 rmse 6.06 0.560 Preprocessor1_Model03
## 2 329 27 2 rmse 6.11 0.597 Preprocessor1_Model07
## 3 1788 14 6 rmse 6.25 0.580 Preprocessor1_Model04
## 4 1427 24 4 rmse 6.39 0.598 Preprocessor1_Model06
## 5 779 36 8 rmse 6.48 0.643 Preprocessor1_Model09Para interpretação dos resultados temos que quanto menor for o RMSE melhor é o modelo. Seleciona-se o melhor modelo usando a função select_best().
6.5.3 Seleção do melhor modelo
xgb_best_tune <- select_best(xgb_trained, 'rmse')
final_xgb_model <- xgb_model %>%
finalize_model(xgb_best_tune)
xgb_best_tune## # A tibble: 1 × 7
## trees min_n tree_depth learn_rate loss_reduction sample_size .config
## <int> <int> <int> <dbl> <dbl> <dbl> <chr>
## 1 920 10 7 0.0309 0.0000360 0.726 Preprocessor1_Mo…select(xgb_best_tune, trees, min_n, tree_depth, .config)## # A tibble: 1 × 4
## trees min_n tree_depth .config
## <int> <int> <int> <chr>
## 1 920 10 7 Preprocessor1_Model03O melhor modelo foi o modelo 3 com RMSE de 6.06.
6.5.4 Aplicando os dados de teste ao modelo
Na etapa final é criado o novo fluxo de trabalho onde é submetido os dados de teste ao modelo escolhido após o treinamento do modelo. É adicionado em add_recipe() o pré-processamento dos dados criado na etapa inicial do pré-processamento, em add_model() é adicionado o modelo final. A função last_fit() indica que é último ajuste a ser realizado.
previsoes <- workflow() %>%
add_recipe(pre_recipe) %>%
add_model(final_xgb_model) %>%
last_fit(divisao) Usando collect_predictions() obtêm-se as previsões salva no objeto previsoes.
previsoes %>% collect_predictions()## # A tibble: 103 × 5
## id .pred .row Price_house .config
## <chr> <dbl> <int> <dbl> <chr>
## 1 train/test split 43.0 2 42.2 Preprocessor1_Model1
## 2 train/test split 27.4 6 32.1 Preprocessor1_Model1
## 3 train/test split 48.4 8 46.7 Preprocessor1_Model1
## 4 train/test split 16.0 9 18.8 Preprocessor1_Model1
## 5 train/test split 22.6 10 22.1 Preprocessor1_Model1
## 6 train/test split 40.9 13 39.3 Preprocessor1_Model1
## 7 train/test split 39.3 16 50.5 Preprocessor1_Model1
## 8 train/test split 40.7 19 42.3 Preprocessor1_Model1
## 9 train/test split 24.2 23 24.6 Preprocessor1_Model1
## 10 train/test split 56.0 24 47.9 Preprocessor1_Model1
## # … with 93 more rowsPode-se visualizar os resultados das previsões em .pred e comparar com os valores originais (Price_house) da base de dados de teste. A Figura 6.6 retorna a reta ajustada dos valores preditos vs valores reais.
previsoes %>%
collect_predictions() %>%
select(.row, Price_house, .pred) %>%
ggplot() +
aes(x = Price_house, y = .pred) +
geom_point() +
geom_abline() 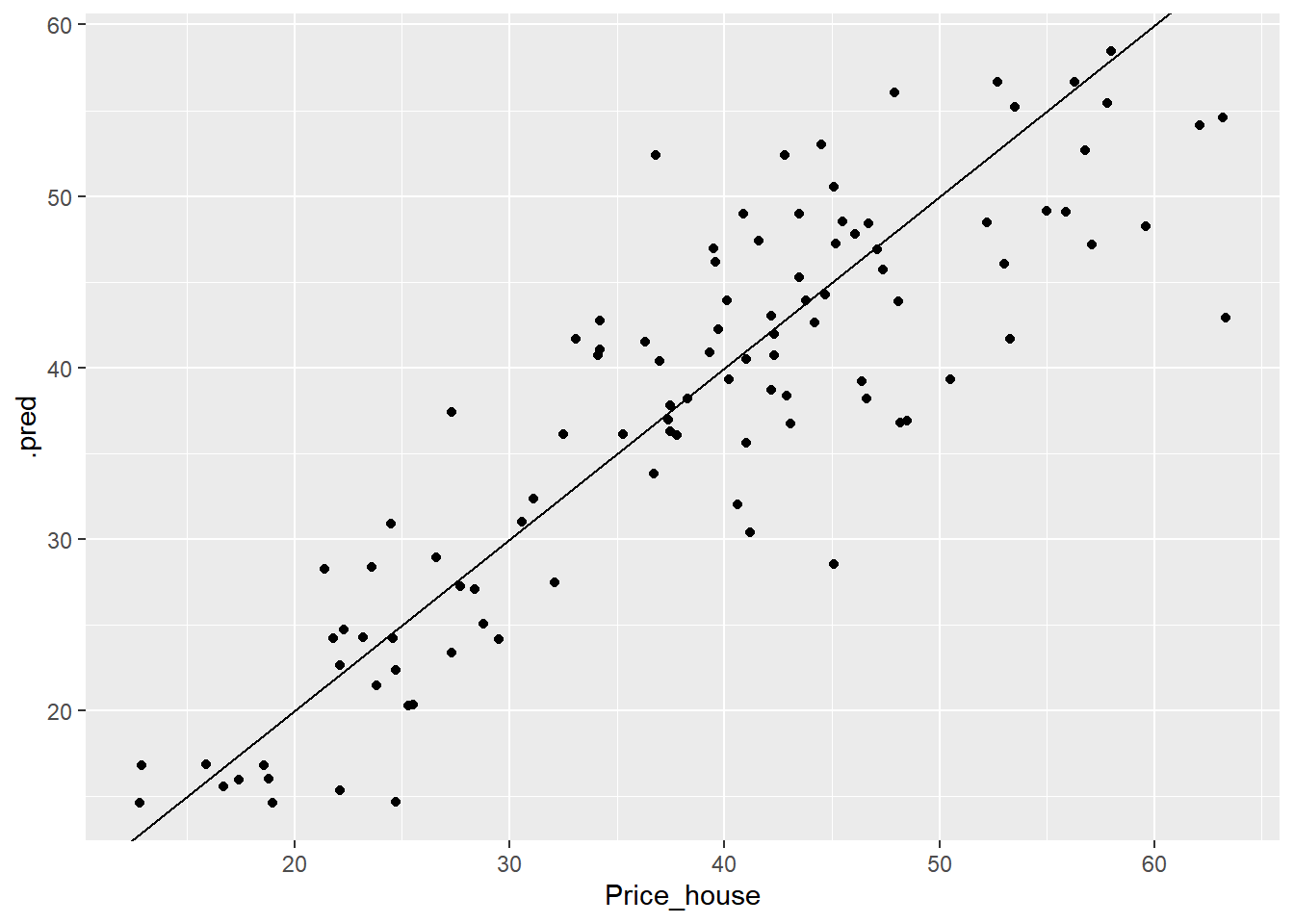
Figure 6.6: Valores preditos vs Valores observados com XGBoost.
Obtendo o RSME para os dados de teste.
previsoes %>% collect_metrics("rmse")## # A tibble: 2 × 4
## .metric .estimator .estimate .config
## <chr> <chr> <dbl> <chr>
## 1 rmse standard 6.13 Preprocessor1_Model1
## 2 rsq standard 0.760 Preprocessor1_Model1O RMSE para o XGBoost aplicado aos dados de teste foi de 6.13, ou seja, houve um aumento se comparado com o resultado nos dados de treino.
Comparando os algoritmos utilizados na regressão, o algoritmo Random Forest obteve um melhor resultado com RMSE menor tanto nos dados de treino como nos dados de teste. O resumo dos resultados podem ser visualizados na Tabela 6.1.
| Algoritmos | Modelo | RMSE_treino | Erro | RMSE_teste |
|---|---|---|---|---|
| Regressão Linear | Modelo 1 | 7.84 | 0.534 | 7.77 |
| Random Forest | Modelo 3 | 5.93 | 0.526 | 5.32 |
| XGBoost | Modelo 3 | 6.06 | 0.560 | 6.13 |
Os algoritmos Random Forest e XGBoost obtiveram um desempenho melhor que a Regressão Linear, sendo neste caso o Random Forest aquele que teve um melhor desempenho. Conclui-se que algoritmos mais robustos baseados em árvores de decisão são melhores preditores para regressão em Machine Learning.