Chapter 7 Einfaktorielle Varianzanalyse
7.1 Vom t-Test zur ANOVA
7.1.1 Einführung
In Kapitel 10 haben wir über ein inferenzstatistisches Verfahren gelernt, die für den Mittelwertsvergleich von zwei unabhängigen Stichproben genutzt werden kann, nämlich den Zweistichproben-t-Test für unabhängige Stichproben. Es ist möglich, wie bei der Regression eine Modellgleichung für die Messwerte von Personen aufzustellen:
\(y_{i1}=\mu_{1}+\epsilon_{i1}\)
\(y_{i2}=\mu_{2}+\epsilon_{i2}\)
Die beiden Gleichungen stehen jeweils für den Messwert einer Person in den entsprechenden Gruppen, die miteinander verglichen werden. So steht \(\mu_{1}\) für den Gruppenmittelwert der ersten Gruppe, wobei \(\mu_{2}\) für den Gruppenmittelwert der zweiten Gruppe steht. \(\epsilon_{i1}\) bzw. \(\epsilon_{i2}\) steht für die Abweichung des Messwerts der i-ten Person in der ersten oder zweiten Gruppe vom Mittelwert \(\mu_{1}\) oder \(\mu_{2}\) der jeweiligen Gruppe. Formal ist das Residuum \(\epsilon\) folgendermaßen definiert: \(\epsilon_{ik}=y_{ik}-\mu_{k}\).
Es ist möglich, die Gruppenmittelwerte aufzuteilen in den sogenannten Gesamtmittelwert und dem Treatmenteffekt-Parameter: \(\mu_{k}=\mu+\alpha_{k}\). Folglich kann man die Modellgleichung auch so angeben:
\(y_{i1}=\mu_{1}+\epsilon_{i1}=\mu+\alpha+\epsilon_{i1}\)
\(y_{i2}=\mu_{2}+\epsilon_{i2}=\mu+\alpha+\epsilon_{i2}\)
Was sind aber nun der Gesamtmittelwert und der Treatmenteffekt-parameter? Der Gesamtmittelwert (im englischen Grand Mean) ist nichts anderes als der Mittelwert aller Messwerte, in welchem nicht zwischen den Gruppenunterschieden differenziert wird. Stellt euch vor, ihr erfasst den IQ bei Engländern und Deutschen. So könnt ihr für die beiden Stichproben einen Gruppenmittelwert \(\mu_{1}\) und \(\mu_{2}\) berecnen. Darüber hinaus könnt ihr einen Gesamtmittelwert bilden, in welchem die IQ-Werte von den Briten und den Deutschen einfließt: Dabei wird nicht zwischen den beiden Nationalitäten differenziert. Bei gleich großen Stichproben kann man den Gesamtmittelwert über folgende Formel berechnen: \(\mu=\frac{\mu_{1}+\mu_{2}}{2}\). Der Treatmenteffekt-Parameter repräsentiert den Effekt der Gruppenzugehörigkeit auf den Gesamtmittelwert. Stellen wir uns vor, der Gesamtmittelwert für den IQ liegt bei \(110\) und die beiden Gruppenmittelwerte sind \(\mu_{1}=105\) für die Engländer und \(\mu_{2}=115\) für die Deutschen. Aus diesen Werten erkennt man, dass die Gruppenzugehörigkeit Auswirkungen auf den mittleren IQ haben: Denn wenn es keinen Einfluss gäbe, müssten die drei Mittelwerte identisch sein! Diese Abweichung der Gruppenmittelwerte vom Gesamtmittelwert wird durch den Treatmeneffekt-Parameter quantifiziert mit folgender Formel: \(\alpha_{k}=\mu_{k}-\mu\). Für die Engländer kriegen wir also einen Treatmenteffekt-Wert von \(\alpha_{1}=105-110=-5\) und für die Deutschen \(\alpha_{2}=115-110=5\). Im nächsten Abschnitt werden die Elemente der Modellgleichung an einem Beispiel anschaulich erklärt. Falls ihr alles bisher verstanden habt, könnt ihr diesen jedoch überspringen. Es wird nichts neues erläutert.
7.1.2 Modellgleichung anhand von einem Beispiel
Stellen wir uns vor, wir möchten die Extraversion von Frankfurtern mit denen von Offenbachern vergleichen. Dafür erstellen wir folgende Tabelle, wobei ein höherer Extraversionswert für eine höhere Extraversion steht):
| Stadt 1=Offenbach und 2= Frankfurt | Extraversion |
|---|---|
| 1 | 1 |
| 1 | 3 |
| 1 | 5 |
| 2 | 6 |
| 2 | 7 |
| 2 | 8 |
Zuallererst berechnen wir den Gesamtmittelwert:
\(\mu=\frac{1+3+5+6+7+8}{6}=5\)
Als nächstes berechnen wir die jeweiligen Gruppenmittelwerte für die Frankfurter und Offenbacher, womit wir dann auch die Treatmenteffekt-Parameter bestimmen können:
\(\mu_{1}=\frac{1+3+5}{3}=3\) und somit \(\alpha_{1}=3-5=-2\)
\(\mu_{2}=\frac{6+7+8}{3}=7\) und somit \(\alpha_{2}=7-5=2\)
Mit diesen Informationen können wir nun die Modellgleichung aufstellen:
\(y_{i1}=3+\epsilon_{i1}=5-2+\epsilon_{i1}\) und
\(y_{i2}=7+\epsilon_{i2}=5+2+\epsilon_{i2}\)
Um die Residuenwerte zu erhalten, müssten wir die Abweichungen der individuellen Messwerte von den Gruppenmittelwerten bestimmen. Dies wird in der folgenden Tabelle dargestellt:
| Gruppenzugehörigkeit | \(y_{ik}\) | \(=\mu_{k}\) | \(+\epsilon_{ik}\) | \(=\mu\) | \(+\alpha_{k}\) | \(+\epsilon_{ik}\) |
|---|---|---|---|---|---|---|
| 1 | 1 | =3 | +(-2) | =5 | -2 | +(-2) |
| 1 | 3 | =3 | +0 | =5 | -2 | +0 |
| 1 | 5 | =3 | +2 | =5 | -2 | +2 |
| 2 | 6 | =7 | -1 | =5 | +2 | -1 |
| 2 | 7 | =7 | +0 | =5 | +2 | +0 |
| 2 | 7 | =7 | +1 | =5 | +2 | +1 |
7.1.3 Die einfaktorielle ANOVA
In der psychologischen Forschung kann es oft dazu kommen,dass man sich nicht nur dafür interessiert, wie groß der Unterschied zwischen zwei Gruppen ist, sondern stattdessen möchte man untersuchen, ob es global Mittelwertsunterschiede zwischen mehreren Gruppen gibt. Stellt euch vor, ihr möchtet nicht nur Frankfurter und Offenbacher miteinander vergleichen, sondern auch Düsseldorfer oder Berliner mituntersuchen. In diesem Fall sind die Mittel des __Zweistichprobe_-t-Tests ausgeschöpft. Jedoch gibt es für diesen Fall eine allgemeine Form der Mittelwertsvergleiche für eine x-beliebige Anzahl an Gruppen, und zwar die einfaktorielle (manchmal auch unifaktoriell genannt) ANOVA. Dabei wird die Idee der t-Tests erweitert auf den Mittelwertsvergleich von k-Gruppen: Die Nullhypothese sagt aus, dass es global auf Populationsebene keine Unterschied zwischen den Gruppenmittelwerten gibt (\(H_{0}:\mu_{1}=\mu_{2}=...=\mu_{k}\)), wobei die Alternativhypothese aussagt, dass mindestens zwei Gruppen sich in ihren Mittelwerten voneinander unterscheiden (\(H_{1}:\mu_{j}\neq \mu_{k}\) für mind. 2 Gruppen j und k). Es handelt sich somit bei der ANOVA um einen Omnibus Test, da mit dem Test __global untersucht wird, ob sich die Mittelwerte der K Gruppen voneinander unterscheide_. Die Modellgleichung der ANOVA ist praktisch identisch mit der des t-Tests, da sie mathematisch identisch sind, wobei bei der ANOVA auf K Gruppen verallgemeinert wird:
\(y_{ik}=\mu_{k}+\epsilon_{ik}=\mu+\alpha_{k}+\epsilon_{ik}\)
Die Definition der einzelnen Elementen bleibt hierbei unverändert:
\(\mu\) steht für den Gesamtmittelwert, in welchem der Mittelwert unabhängig von der Gruppenzuweisun berechnet wird.
\(\mu_{k}\) steht für die Gruppenmittelwerte der K Gruppen, die miteinander verglichen werden
\(\alpha_{k}\) steht für den Treatment-Effekt, welcher durch die Gruppenzugehörigkeit entsteht (\(\alpha_{k}=\mu_{k}-\mu\))
Im Folgenden werden verschiedene mathematische Beziehungen zwischen den Elementen des Modells veranschaulicht:
1.) Nebenbedingung: Es gilt ausnahmslos, dass die Summe aller Treatmenteffekt-Parameter Null ergibt (\(\alpha_{1}+\alpha_{2}+...+\alpha_{k}=0\)). Der Grund hierfür ist relativ simpel: Die Treatmenteffekte repräsentieren die Abweichungen der Gruppenmittelwerte vom Gesamtmittelwert. Da die Gruppenmittelwerte als ,,einzelne Beobachtungen der Gesamtmittelwerte’’ betrachtet werden können, gilt für Abweichungen von diesem Gesamtmittelwert folgende allgemeine Eigenschaft von Mittelwerten: \(\sum_{m=1}^{n}(x_{m}-\overline{x})=0\). Deshalb ist die Summe der Parameter Null.
2.) Messwert- Gesamtmittelwert= Treatmenteffekt+ Residuum bzw \(y_{ik}-\mu=\alpha_{k}+\epsilon_{ik}\): Dieser Zusammenhang erscheint plausibel, da man diesen mathematisch beweisen kann:
Vorbereitung: Es gilt: \(y_{ik}=\mu+\alpha_{k}+\epsilon_{ik}\)
\(y_{ik}-\mu\) / Wir ersetzen \(y_{ik}\) durch die obige Formel
\(\mu+\alpha_{k}+\epsilon_{ik}-\mu=\alpha_{k}+\epsilon_{ik}\)
7.2 Einfaktorielle ANOVA: Durchführung
7.2.1 Voraussetzungen und Forschungslogik
Eine grundlegende Voraussetzung bei der einfaktoriellen ANOVA (oder zumindest für die Form der Varianzanalyse, welche wir im folgenden betrachten) ist, dass die Stichproben unabhängig voneinander sind. Folglich dürfen Probanden nur Mietglied einer Gruppe sein und die Gruppen dürfen sich nicht systematisch beeinflussen (Unabhängigkeit der Beobachtungseinheiten). Eine weitere Voraussetzung ist, dass innerhalb jeder Gruppe die Werte der abhängigen Variable normalverteilt sind. Darüber hinaus müssen auch die Varianzen der K Gruppen gleich sein (Varianzhomogenität/Homoskedastizität). Die ANOVA ist relativ robust gegenüber Verletzungen der Normalverteilungsannahme, jedoch nicht gegenüber Verletzungen der Homoskedastizitätsannahme. Problematisch ist dies vor allem, wenn die relativ zu den anderen kleiner besetzten Gruppen die größere Varianzen aufweisen. Durch diesen Umstand resultiert, dass die ANOVA einen höheren \(\alpha\)-Fehler hat bzw. dass die Wahrscheinlichkeit steigt, fälschlicherweise ein signifikantes Ergebnis zu generieren. Es gibt jedoch spezielle Formen der ANOVA, bei welchem die Verletzung der Homogenitätsannahme berücksichtigt wird.
Oben im Text wurden bereits die Null- und Alternativhypothese der einfaktoriellen ANOVA definiert: Wenn die \(H_{0}\) beibehalten wird, bedeutet dies, dass die empirisch erfassten Gruppenunterschiede in den Mittelwerten das Resultat der zufälligen Stichprobenziehung ist bzw. per Zufall entstanden ist. Wenn die \(H_{0}\) jedoch verworden wird, bedeutet dies, dass die erfassten Gruppenunterschiede im Mittelwert nicht allein als das Resultat einer zufälligen Ziehung interpretiert werden kann. So schließen wir daraus, dass auf Populationsebene tatsächlich mindestens 2 Gruppen gibt, die sich in ihren Mittelwerten unterscheiden.
7.2.2 Quadratsummen
Ähnlich wie bei der multiplen Regression kann man die Variation im Kriterium durch Quadratsummen darstellen und diese auch in mehrere Quadratsummen zerlegen. Bevor wir dies tun, betrachten wir, wie man den Messwert einer Person i in der Gruppe k als eine Summe von drei Komponenten darstellen kann:
Messwert\(=\) Stichprobengesamtmittelwert + Stichproben-Treatmenteffekt + Residuum
bzw. \(y_{ik}=\overline{\overline{y}}+(\overline{y_{k}}-\overline{\overline{y}})+(y_{ik}-\overline{y_{k}})\)
Dabei ist \(\overline{\overline{y}}\) definiert als die Gesamtmittelwert der Stichprobe bzw. der Mittelwert aller Gruppenmittelwerte: \(\overline{\overline{y}}=\frac{1}{N}\sum_{k=1}^{K}\sum_{i=1}^{n_{k}}y_{ik}\)
WICHTIGE ANMERKUNG: Das \(N\) in der Formel zur Berechnung des Gesamtmittelwerts steht für die Gesamtstichprobengröße. Wenn wir 20 Düsseldorfer, 20 Frankfurter und 20 Offenbacher miteinander vergleichen, ist die Gesamtstichprobengröße \(N=60\). Der spezifische Gruppenmittelwert ist \(\overline{y_{k}}\) der folgendermaßen berechnet wird: \(\overline{y_{k}}=\frac{1}{{k}}\sum_{i=1}^{{k}}y_{ik}\)
Aus dieser Zerlegung der Komponenten kann man die Quadratsummenzerlegun ableiten:
\(QS_{tot}=QS_{zw}+QS_{inn}\) bzw.
\(\sum_{k=1}^{K}\sum_{i=1}^{n_{k}}(y_{ik}-\overline{\overline{y}})^2=\sum_{k=1}^{k}n_{k}\cdot (\overline{y_{k}}-\overline{\overline{y}})^2+\sum_{k=1}^{k}\sum_{i=1}^{n_{k}}(y_{ik}-\overline{y_{k}})\)
Dabei steht \(QS_{tot}=\sum_{k=1}^{K}\sum_{i=1}^{n_{k}}(y_{ik}-\overline{\overline{y}})^2\) für die totale Quadratsumme bzw. die totale Variation der Messwerte um den Gesamtmittelwert. Sie wird quantifiziert über die quadrierten Abweichungen der Messwerte vom Gesamtmittelwert. \(QS_{zw}=\sum_{k=1}^{k}n_{k}\cdot (\overline{y_{k}}-\overline{\overline{y}})^2\) quantifiziert die Variation der Gruppenmittelwerte um den Gesamtmittelwert, d.h. es handelt sich hierbei um die Quadratsumme zwischen den Gruppen. Zuletzt stellt \(QS_{inn}=\sum_{k=1}^{k}\sum_{i=1}^{n_{k}}(y_{ik}-\overline{y_{k}})\) die Quadratsummen innerhalb der Gruppen dar bzw. quantifiziert die Variation der Messwerte innerhalb der Gruppen (um den Gruppenmittelwert herum). Wie bei der multiplen Regression haben auch hier die Quadratsummen Freiheitsgrade: Die Quadratsumme zwischen den Gruppen hat \(df_{zw}=K-1\) Freiheitsgrade, wobei K für die Anzahl der Gruppen steht Die Quadratsumme innerhalb der Gruppen hat \(df_{inn}=N-K\) Freiheitsgrade, wobei N die Gesamtstichprobengröße und K die Anzahl der Gruppen ist. Die Quadratsummmen und ihre Freiheitsgrade werden zur Berechnung der F-Prüfgröße herangezogen. Im folgenden wird dies an einem Beispiel veranschaulicht.
7.2.3 Mittlere Quadratsummen und die F-Prüfgröße
Stellt euch vor, ihr möchtet schauen, wie das Lieblingsmusikgenre die Gewissenhaftigkeit von Personen beeinflusst. Dafür habt ihr mehrere Personen hinsichtlich ihrem Musikgeschmack und ihrer Gewissenhaftigkeit abgefragt und folgende Tabelle erstelle (Geht dabei davon aus, dass die Voraussetzungen der einfaktoriellen ANOVA erfüllt sind.:
| Heavy Metal | Elektro | Jazz | Pop | |
|---|---|---|---|---|
| Gewissenhaftigkeit | 5 | 4 | 1 | 3 |
| 3 | 3 | 0 | 2 | |
| 5 | 3 | 2 | 5 | |
| 5 | 2 | 1 | 4 |
Zuallererst berechnen wir die Gruppenmittelwerte, Gesamtmittelwerte, sowie die verschiedenen Quadratsummen:
1.) Gruppenmittelwerte und Gesamtmittelwert:
\(\overline{x_{1}}=\frac{5+3+5+5}{4}=4.5\)
\(\overline{x_{2}}=\frac{4+3+3+2}{4}=3\)
\(\overline{x_{3}}=\frac{1+0+2+1}{4}=1\)
\(\overline{x_{4}}=\frac{3+2+5+4}{4}=3.5\)
\(\overline{\overline{y}}=\frac{4.5+3+1+3.5}{4}=3\)
2.) Quadratsummen:
\(QS_{tot}=\sum_{k=1}^{K}\sum_{i=1}^{n_{k}}(y_{ik}-\overline{\overline{y}})^2\)
\(QS_{tot}=(5-3)^2+(3-3)^2+(5-3)^2+(5-3)^2+(4-3)^2+(3-3)^2+(3-3)^2+(2-3)^2+(1-3)^2+(0-3)^2+(2-3)^2+(1-3)^2+(3-3)^2+(2-3)^2+(5-3)^2+(4-3)^2\)
\(QS_{tot}=4+0+4+4+1+0+0+1+4+9+1+4+0+1+4+1=38\)
\(QS_{zw}=\sum_{k=1}^{k}n_{k}\cdot (\overline{y_{k}}-\overline{\overline{y}})^2\)
\(QS_{zw}=4\cdot(4.5-3)^2+4\cdot (3-3)^2+4\cdot (1-3)^2+4\cdot (3.5-3)^2\)
\(QS{zw}=9+ 0+ 16+1=26\)
\(QS_{inn}=QS_{tot}-QS_{zw}=38-26=12\)
Man kann nun mit Hilfe der Quadratsummen die mittleren Quadratsummen berechnen, welche zur Berechnung der F-Prügröße benötigt werden. Über folgende Formeln werden die mittleren Quadratsummen berechnet:
\(MQS_{zw}=QS_{zw}/df_{zw}=26/(K-1)=26/3=8.67\)
\(MQS_{inn}=QS_{inn}/df_{inn}=12/(N-K)=12/12=1\)
Nun können wir mit diesen Informationen die F-Prüfgröße bestimmen. Zur Erinnerung: Unsere Nullhypothese besagt, dass es über alle Gruppen hinweg keine Mittelwertsunterschiede gibt. Für unser Beispiel bedeutet dies, dass das Lieblingsmusikgenre im Mittel keine Auswirkungen auf die Gewissenhaftigkeit hat. Die Alternativhypothese besagt, dass mind. zwei Gruppen sich im Mittel voneinander unterscheiden. Die F-Prüfgröße wird über folgende Forml berechnet:
\(F=\frac{MQS_{zw}}{MQS_{inn}}=\frac{8.67}{1}=8.67\)
Nun müssen wir überprüfen, ob die F-Prüfgröße signifikant ist. Dies erreicht man, indem man die F-Prügröße \(8.67\) mit dem kritischen Wert unter der F-Verteilung vergleicht mit \(df_{zw}\) als Zählerfreiheitsgrad und \(df_{inn}\) als Nennerfreiheitsgrad. Wenn die F-Prüfgröße größer als der kritische F-Wert ist, also \(F>F_{df_{zw},df_{inn},\alpha}\) gilt, ist das Ergebnis signifikant. In unserem Beispiel haben wir \(df_{zw}=3\) und \(df_{inn}=12\) Freiheitsgrade: Somit lautet unser kritischer Wert:
## [1] 3.490295Da unsere Prügröße größer bzw. extremer als der kritische Wert ist, wird die Nullhypothese verworfen, d.h. im Mittel unterscheiden sich mindestens zwei Gruppen signifikant voneinander. Für unser Beispiel bedeutet dies, dass mit einer Irrtumswahrscheinlichkeit von 5% sich die Personen in mindestens zwei Musikgenren im Mittel in der Gewissenhaftigkeit voneinander unterscheiden. Welche Gruppen sich konkret unterscheiden, kann durch die ANOVA nicht festgestellt werden.
7.2.4 ANOVA in R
Es ist möglich, mit dem ezANOVA()-Befehl in R, welches im ez package liegt, eine einfaktorielle ANOVA durchzuführen.
# Datensatz
data<- data.frame(id=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16),
genre=c('heavy','heavy','heavy','heavy',
'elektro','elektro','elektro','elektro',
'jazz','jazz','jazz','jazz',
'pop','pop','pop','pop'),
gewis=c(5,3,5,5,4,3,3,2,1,0,2,1,3,2,5,4))
# id und genre zu Faktoren konvertieren
data$id<- as.factor(data$id)
data$genre<- as.factor(data$genre)
# Package laden (vorher vllt. installieren mit install.packages())
library('ez')## Registered S3 methods overwritten by 'lme4':
## method from
## cooks.distance.influence.merMod car
## influence.merMod car
## dfbeta.influence.merMod car
## dfbetas.influence.merMod carezANOVA(data= data, # Datensatz, welcher genutzt wird
wid= id, # Variable zur Identifikation der Probanden
dv= gewis, # Die abhängige Variable
between=genre) # Die Gruppierungsvariable, die zwischen Personen unterscheidet## Coefficient covariances computed by hccm()## $ANOVA
## Effect DFn DFd F p p<.05 ges
## 1 genre 3 12 8.666667 0.002482849 * 0.6842105
##
## $`Levene's Test for Homogeneity of Variance`
## DFn DFd SSn SSd F p p<.05
## 1 3 12 0.75 6 0.5 0.68926947.2.5 Bedeutung der mittleren Quadratsummen
Die mittleren Quadratsummen repräsentieren in der ANOVA relative Unterschiede zwischen Gruppen bzw. Personen. Um es kurz zu fassen, quantifiziert die mittlere Quadratsumme \(QS_{zw}\) die gruppenspezifischen Unterschiede, d.h. sie beschränkt sich auf die Unterschiede der Mittelwerte vom Gesamtmittelwert, relativiert an ihren Freiheitsgraden. Wenn die Gruppen gleichbesetzt sind, besteht folgender Zusammenhang: \(MQS_{zw}=Var(\epsilon)+n\cdot Var(\alpha)\). Die mittlere Quadratsumme \(MQS_{inn}\) repräsentiert die personenspezifische Unterschiede, d.h. sie beschränkt sich allein auf die Abweichungen der Messwerte von ihrem Gruppenmittelwert, relativiert an ihren Freiheitsgraden. Gleichzeitig ist \(MQS_{inn}\) ein Schätzer für die Residualvarianz: \(MQS_{inn}\approxeq Var(\epsilon)\).
7.2.6 \(\alpha\)-Fehlerinflation
Man könnte nun meinen, dass die einfaktorielle Varanzanalyse komplett überflüssig ist, da sie zum einen keine Auskunft darüber gibt, welche zwei Gruppen sich im Mittel voneinander unterscheiden und zum anderen kann man eine ANOVA durch mehrere t-Tests ersetzen kann. Jedoch ist die m-fache Anwendung eines t-Tests mit mehreren PRoblemen verbunden, das größte davon ist die sogenannte \(\alpha\)-Fehler-Inflation. Wenn wir den multiplen \(\alpha\)-Fehler definieren als die Wahrscheinlichkeit, dass von mehrerehn t-Tests bei mindestens einem die \(H_{0}\) verworfen wird, obwohl in allen Tests die Nullhypothese gilt, können wir bei einer m-fachen Anwendung eines t-Tests folgenden Umstand feststellen: Der multiple \(\alpha\)-Fehler liegt deutlich oberhalb desjenigen \(\alpha\)-Fehlers, welchen wir für die einzelnen Tests festgelegt haben, und kann im Extremfall bis zum m-fachen des einzelnen \(\alpha\)-Fehlers ansteigen. Dies bedeutet, dass die Wahrscheinlichkeit, mind. einmal einen \(\alpha\)-Fehler zu begehen, rasant ansteigt. Stellen wir uns vor, wir möchten drei verschiedene t-Tests auf einem 5%-\(\alpha\)-Fehlerniveau anwenden. So kann der multiple \(\alpha\)-Fehler im Extremfall bei 15% liegen, d.h. die Wahrscheinlichkeit dass mindestens einer dieser drei t-Tests signifikant ausfällt, liegt bei 15%. Es gibt Korrekturformeln, um das Problem der \(\alpha\)-Fehler-Inflation zu umgehen. Eine solche Methode stellt die Bonferroni Korrektur dar. Bei der Bonferroni-Korrektur wird der \(\alpha\) Fehler von jedem einzelnen Testverfahren korrigiert in Abhängigkeit von der Anzahl der zu durchführenden Tests nach folgender Formel: \(\alpha_{b}=\alpha/m\). Bei unserem Beispiel würden wir für dreit t-Tests folgenden korrigierten \(\alpha\)-Fehler haben: \(\alpha_{b}=0.05/3=0.0167\). Mit der Bonferroni-Korrektur wird folglich gewährleistet, dass der multiple \(\alpha\)-Fehler niemals größer sein wird als den ursprünglich für das Testverfahren gewählte \(\alpha\)-Fehler. Der Nachteil der Bonferroni-Korrektur ist, dass die Teststatistik nun konservativer ist, wodurch sich die Teststärke verringert, d.h. es wird schwieriger, einen tatsächlich vorhandenen Effekt aufzudecken. Deshalb ist die ANOVA die bessere Wahl, da es sich hierbei um einen globalen Test handelt, welcher alle Mittelwerte simultan testet und den vom Testanwender gewählten \(\alpha\)-Fehler einhält.
7.3 Post-Hoc Tests
Kommen wir zurück zu unserem Beispiel mit dem Lieblingsmusikgenre. Wir haben nun eine signifikante ANOVA erhalten, was bedeutet, dass sich mind. zwei Gruppen im Mittel voneinander unterscheiden. Nun gilt es herauszufinden, welche Gruppen dies spezifisch sind. Hier greift man nun auf sogenannte Post-Hoc Tests, die unterschuchen, welche Paare von Gruppen einen signifikanten Mittelwertsunterschied aufweisen. Ein solcher Post-Hoc Test ist der Tukey-Test, welchen wir im folgenden vorstellen werden.
7.3.1 Tukey-Test
7.3.1.1 Logik der Tukey Methode
Beim Tukey-Test werden im ersten Schritt alle möglichen Paare von Gruppen gebildet. Daraufhin wird mit dem Test entschieden, ob die Mittelwertsdifferenz sich zwischen den beiden Gruppen signifikant voneinander unterscheiden. Der Vorteil beim Tukey Test ist, dass der insgesamt ausgewählte \(\alpha\)-Fehler für alle Testvergleiche kontrolliert wird, d.h. es kommt zu keiner Inflation des \(\alpha\)-Fehlers, da ein Gesamt-\(\alpha\)-Fehler ausgewählt wird. Dieser Gesamt-\(\alpha\)-Fehler ist folgendermaßen definiert: Ausgehend von der Annahme der Nullhypothese (\(H_{0}\): In der Population sind die Mittelwerte der Gruppen alle identisch) entspricht die Wahrscheinlichkeit, dass sich mind. ein Gruppenpaar bzw. zwei Gruppen signifikant voneinander unterscheiden, dem Gesamt-\(\alpha\)-Fehler. Für unser Beispiel würden wir folgenden Gruppenpaare bilden: 1.) Heavy Metal und Elektro, 2.) Heavy Metal und Jazz, 3.) Heavy Metal und Pop, 4.) Elektro und Jazz, 5.) Elektro und Pop, 6.) Jazz und Pop. Wichtig: Der Tukey Test setzt voraus, dass in allen Gruppen die Stichprobengrößen identisch sind.
7.3.1.2 Durchführung des Tukey-Tests
Als erstes wird die sogenannte Honest significant difference (HSD, im folgenden \(P_{krit}\)) berechnet nach folgender Formel:
\(P_{krit}=q_{(\alpha;m;df_{inn})}\cdot s_{\overline{y}}\)
Dabei steht q für den kritischen q-Wert unter der sogenannten ,,studentized range’’-Verteilung (auch q-Verteilung genannt). Die q-Verteilung ist abhängig von zwei Parametern: Zum einen von den Anzahl der Gruppenmittelwerten (m) und zum anderen von dem Freiheitsgrad \(df_{inn}\). In unserem Beispiel entspricht \(m=4\) und \(df_{inn}=N-K=16-4=12\). Man kann diesen kritischen Wert aus einer Tabelle herauslesen oder in in R bestimmen über den Befehl qtukey():
qtukey(0.95, # Alpha-Fehlerniveau
nmeans=4, # Anzhal der Gruppenmittelwerte
df=12) # Anzahl der Freiheitsgrade von df(inn)## [1] 4.19866\(s_{\overline{y}}\) kann man über folgende Formel bestimmen: \(s_{\overline{y}}=\sqrt{MQS_{inn}/n}\). Wichtig: n steht in der Formel für die Stichprobengröße innerhalb einer Gruppe, nicht für die Gesamtstichprobengröße. In unserem Beispiel entspricht \(n=4\), da in jeder Gruppe 4 Personen sind. Für unser Beipiel erhalten wir demnach folgende Lösung:
\(s_{\overline{y}}=\sqrt{1/4}=0.5\)
Die Honest Significant Difference beträgt demnach:
\(P_{krit}=4.2\cdot 0.5=2.1\)
Im nächsten, und letzen Schritt, berechnet man nun den Betrag der Mittelwertsdifferenz aller Gruppenpaare (\(|\overline{y}_{j}-\overline{y}_{k}|\) für alle Paare j und k). Die Logik hierbei ist, dass zwei Gruppenmittelwerte sich dann signifikant voneinader unterscheiden, wenn ihre Mittelwertsdifferenz im Betrag größer ist als die Honest Signifikant Difference, also gilt: \(|\overline{y}_{j}-\overline{y}_{k}|>P_{krit}\)
Im Folgenden wird für jedes Gruppenpaar die Mittelwertsdifferenz berechnet und überprüft, ob diese Gruppen sich signifikant voneinander unterscheiden:
1.) Heavy Metal und Elektro: \(|4.5-3|=1.5\) \(\to\) Da \(1.5<2.1\) gilt, ist die Mittelwertsdifferenz unter einem \(\alpha\)-Fehlerniveau von 5% nicht signifikant.
2.) Heavy Metalund Jazz: \(|4.5-1|=3.5\) \(\to\) Da \(3.5>2.1\) gilt, ist die Mittelwertsdifferenz unter einem \(\alpha\)-Fehlerniveau von 5% signifikant.
3.) Heavy Metal und Pop: \(|4.5-3.5|=1\) \(\to\) Da \(1<2.1\) gilt, ist die Mittelwertsdifferenz unter einem \(\alpha\)-Fehlerniveau von 5% nicht signifikant.
4.) Elektro und Jazz: \(|3-1|=2\) \(\to\) Da \(2<2.1\) gilt, ist die Mittelwertsdifferenz unter einem \(\alpha\)-Fehlerniveau von 5% nicht signifikant
5.) Elektro und Pop: \(|3-3.5|=0.5\) \(\to\) Da \(0.5<2.1\) gilt, ist die Mittelwertsdifferenz unter einem \(\alpha\)-Fehlerniveau von 5% nicht signifikant.
6.) Jazz und Pop: \(1-3.5=2.5\) \(\to\) Da \(2.5>2.1\) gilt, ist die Mittelwertsdifferenz unter einem \(\alpha\)-Fehlerniveau von 5% signifikant.
Ergebnis: Die Paare ,,Heavy Metal/Jazz’’ und ,,Pop/Jazz’’ haben sich im Mittel signifikant in ihrer Gewissenhaftigkeit voneinander unterschieden.
7.3.1.3 Tukey Methode in R
Es ist möglich, in R den Tukey Test mit einen Befehl zu berechnen und zwar TukeyHSD():
## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = gewis ~ genre, data = data)
##
## $genre
## diff lwr upr p adj
## heavy-elektro 1.5 -0.5993301 3.59933011 0.2012641
## jazz-elektro -2.0 -4.0993301 0.09933011 0.0636452
## pop-elektro 0.5 -1.5993301 2.59933011 0.8923559
## jazz-heavy -3.5 -5.5993301 -1.40066989 0.0016505
## pop-heavy -1.0 -3.0993301 1.09933011 0.5146067
## pop-jazz 2.5 0.4006699 4.59933011 0.0185992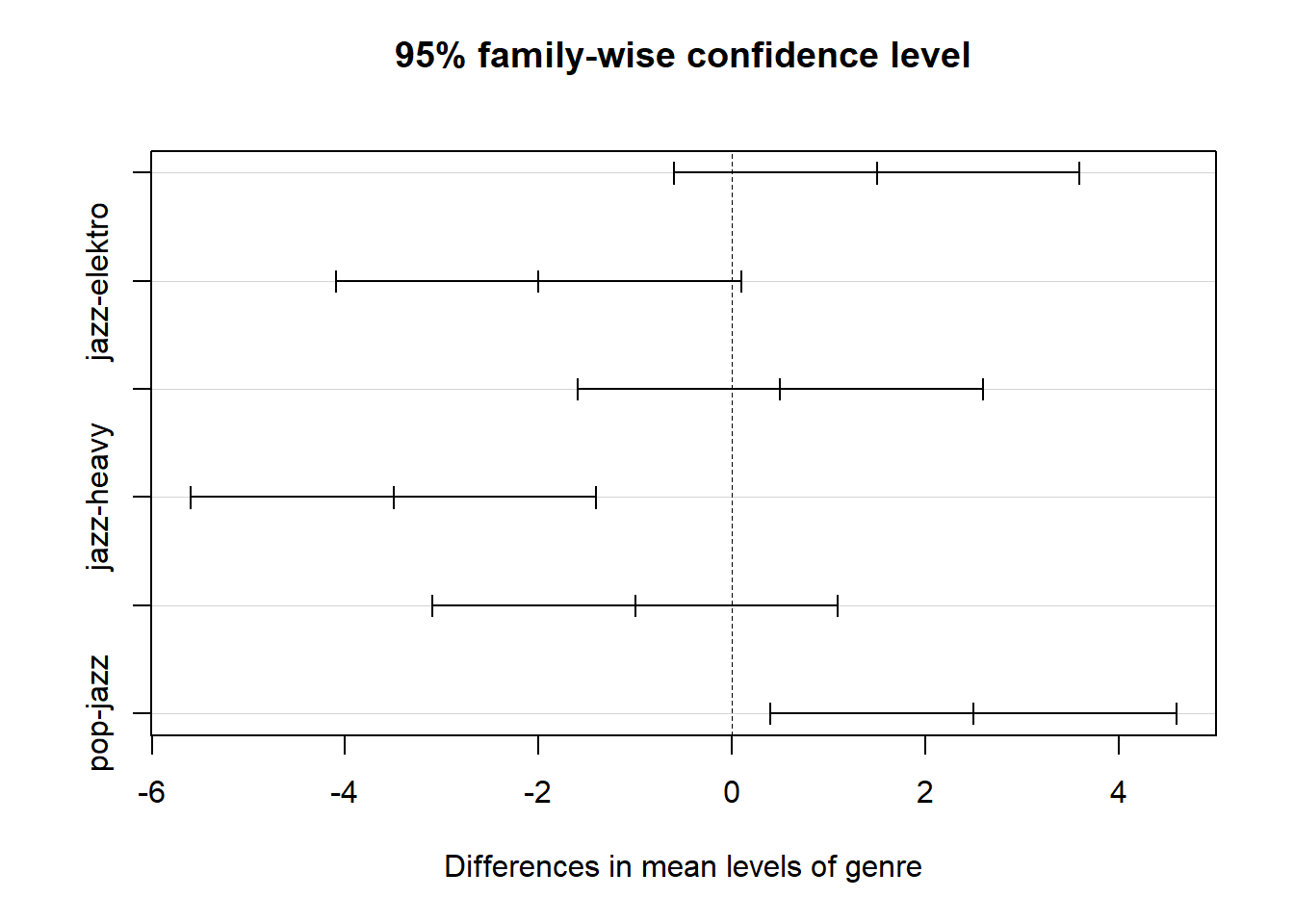
Neben den Mittelwertsdifferenzen der Gruppenpaare (diff-Spalte) und dem p-Wert, welche die Signifikanz der Mittelwertsdifferenz darstellt (p adj-Spalte) gibt der TuckeyHSD Befehl zusätzlich die Konfidenzintervalle für die Mittelwertsdifferenzen an (lwr und upr-Spalte).
7.3.2 Bonferroni Methode in R
Es ist auch möglich, die Bonferroni-Korrektur und folglich die adjustierten t-Tests für alle Gruppenpaare mit einer Formel in R durhzuführen und zwar pairwise.t.test():
pairwise.t.test(data$gewis, # abhängige Variable
data$genre, # Gruppierungsvaraible, Faktorstufen bilden die Gruppenpaare
p.adjust='bonferroni')##
## Pairwise comparisons using t tests with pooled SD
##
## data: data$gewis and data$genre
##
## elektro heavy jazz
## heavy 0.332 - -
## jazz 0.091 0.002 -
## pop 1.000 1.000 0.025
##
## P value adjustment method: bonferroniDie Werte in der Tabelle sind die p-Werte des adjustierten t-Tests bei den jeweiligen Gruppen. Mit der Bonferroni-Methode kommt man zum gleichen Ergebnis: Die Gruppenpaare ,,Heavy Metal und Jazz’’ sowie ,,Jazz und Pop’’ unterscheiden sich im Mittel signifikant voneinander in der Gewissenhaftigkeit.
7.3.3 Vergleich Tuckey und Bonferroni
Die Bonferroni-Methode stellt auch ein Post-Hoc-Methode dar, da man theoretisch gesehen nach einer signifikanten ANOVA mehrere t-Tests für alle Gruppenpaare durchführen könnte, wobei die \(\alpha\)-Fehler bereits korrigiert wurden. Im allgemeinen ist die Tuckey Methode der Bonferroni-Korrektur vorzuziehen, da diese eine höhere Teststärke aufweist aufgrund der Tatsache, dass der Test nicht durch Testlogik selbst konservativer wird.
7.4 Abschließend: Kausale Interpretation und Erweiterung der einfaktoriellen ANOVA
Eine Ablehnung der \(H_{0}\) ist nicht gleichzusetzen mit einer Kausalität: Wir können anhand des signifikanten Ergebnisses nicht sagen, dass das Lieblingsmusikgenre die Ursache für die unterschiedlichen Mittelwerte in der Gewissenhaftigkeit ist. Eine kausale Interpretation ist nur möglich, wenn eine randomisierte Zuordnung der einzelnen Personen zu den Gruppen stattfand. In unserem Beispiel ist dies nicht der Fall, da die Personen sich selbst in die Gruppen eingewählt haben in Abhängigkeit von ihrem Lieblingsmusikgenre. Eine Alternative zur randomisierten Zuordnung ist die Aufnahme passender Kontrollvariablen in das Modell. Da wir in unserem Beispiel dies jedoch nicht gemacht haben, können wir definitiv keine kausalen Interpretationen generieren.
Die einfaktorielle ANOVA kann auch auf mehrere Faktoren erweitert werden. Stellen wir uns vor, wir möchten nicht nur Mittelwertsunterschiede in der Gewissenhaftigkeit in Abhängigkeit vom Lieblingsmusikgenre auf Signifikanz prüfen, sondern auch in Abhängigkeit von der Nationalität. In diesem Fall hätten wir dann zwei Faktoren, die möglicherweise sich auch gegenseitig beeinflussen. Dies entspräche dann einer zweifaktoriellen ANOVA, welche wir im nächsten Kapitel behandeln werden.