Chapter 2 Aula 06 - Exercicios

2.1 Exercicio 01

Vamos carregar o conjunto de dados:

dadosCen01 = read_excel("Dados/Data_HousePrice_Area.xlsx",sheet = 1 )
dadosCen02 = read_excel("Dados/Data_HousePrice_Area.xlsx",sheet = 2 )

Vamos fazer um grafico de dispersao para os dois conjuntos

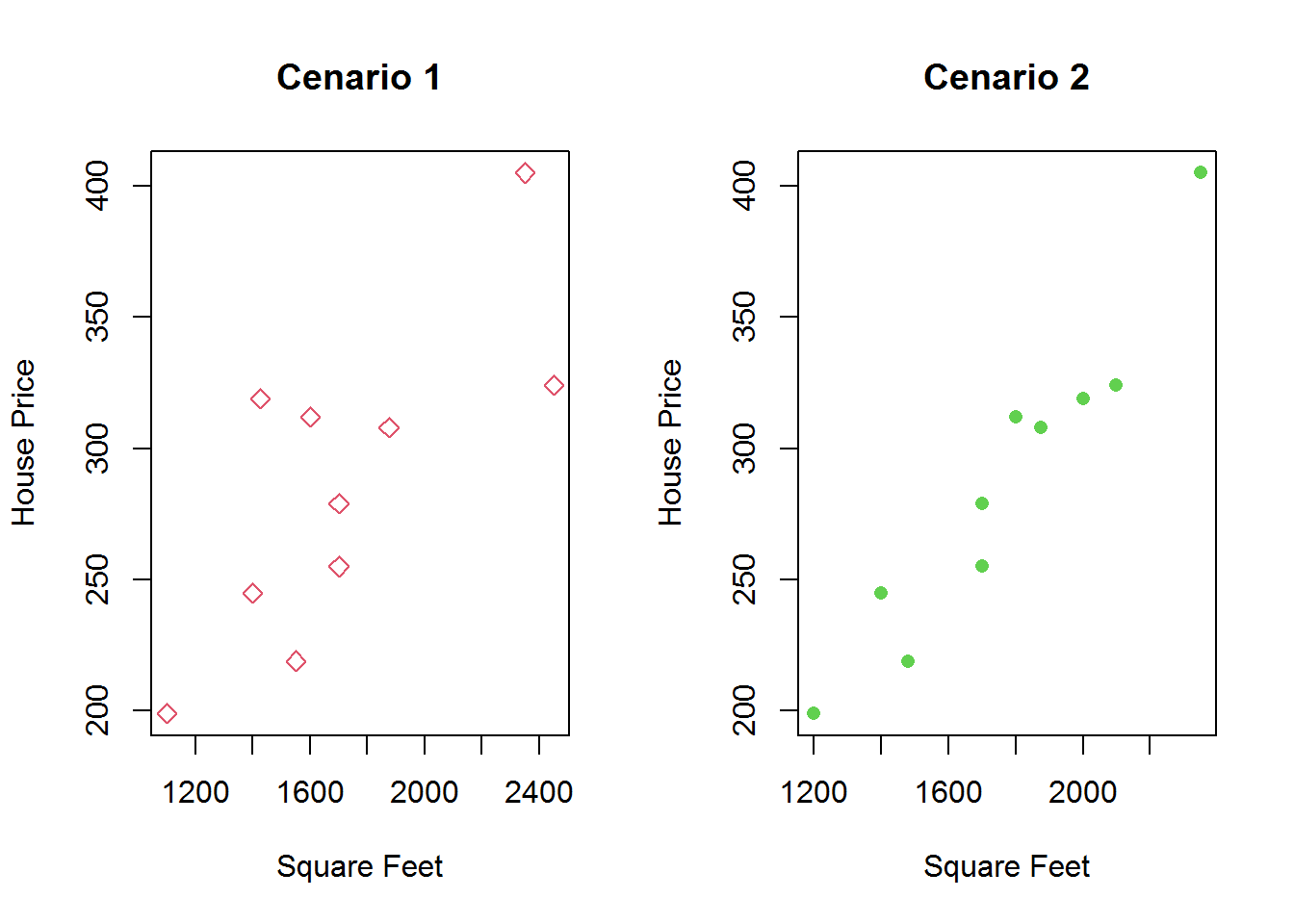
Comparando os dois graficos, podemos observar:

• observação 1
• observação 1

Algumas estatisticas descritivas para House Price::

• Cenário 01:

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   199.0   247.5   293.5   286.5   317.2   405.0

• Cenário 2:

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   199.0   247.5   293.5   286.5   317.2   405.0

Vamos agora ajustar um modelo de regressão para amobos os cenarios

modelCen01 = lm(dadosCen01$`House Price` ~ dadosCen01$`Square Feet`)
sumCen01 = summary(modelCen01)
sumCen01

## 
## Call:
## lm(formula = dadosCen01$`House Price` ~ dadosCen01$`Square Feet`)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -49.388 -27.388  -6.388  29.577  64.333 
## 
## Coefficients:
##                          Estimate Std. Error t value Pr(>|t|)  
## (Intercept)              98.24833   58.03348   1.693   0.1289  
## dadosCen01$`Square Feet`  0.10977    0.03297   3.329   0.0104 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 41.33 on 8 degrees of freedom
## Multiple R-squared:  0.5808, Adjusted R-squared:  0.5284 
## F-statistic: 11.08 on 1 and 8 DF,  p-value: 0.01039

Para o cenario 1, o valor do \(R^2\) é 0.58

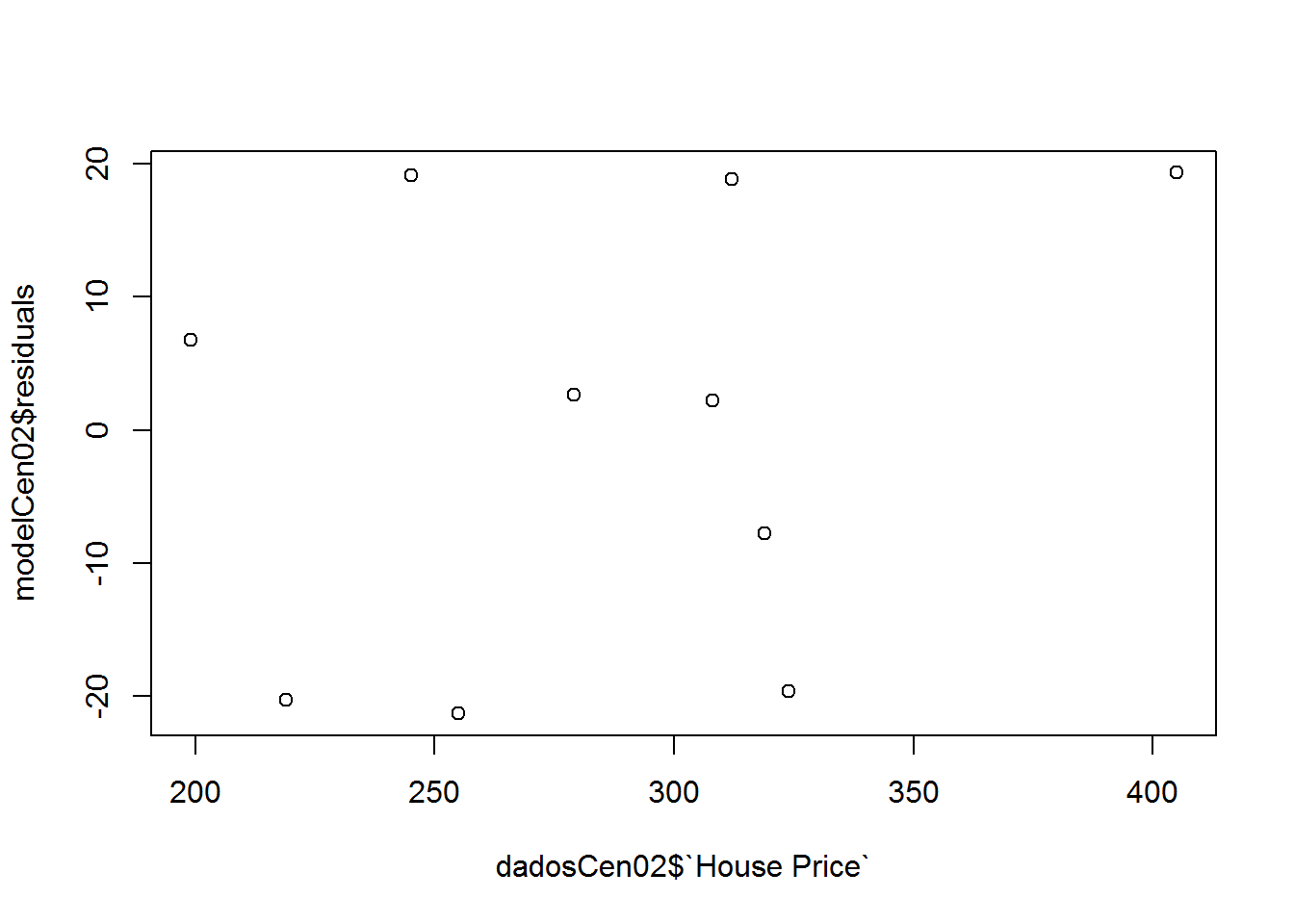
Vamos analisar os residuos:

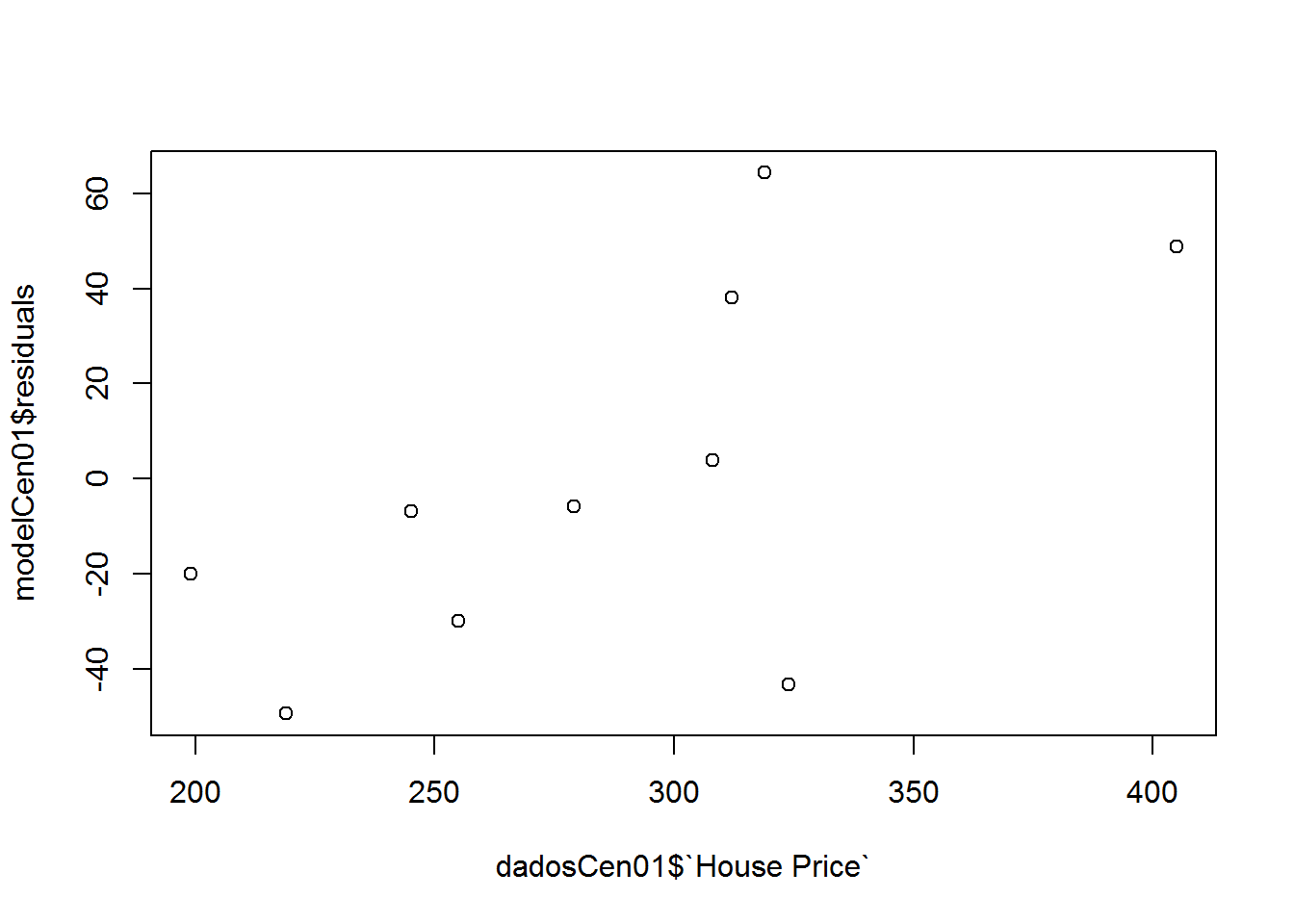
Escrever aqui o que pode ser observado do grafico de residuos

Vamos para o cenario 2:

modelCen02 = lm(`House Price` ~ `Square Feet`, data = dadosCen02)
sumCen02 = summary(modelCen02)
sumCen02

## 
## Call:
## lm(formula = `House Price` ~ `Square Feet`, data = dadosCen02)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -21.323 -16.654   2.458  15.838  19.336 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   -9.64509   30.46626  -0.317     0.76    
## `Square Feet`  0.16822    0.01702   9.886 9.25e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 17.56 on 8 degrees of freedom
## Multiple R-squared:  0.9243, Adjusted R-squared:  0.9149 
## F-statistic: 97.73 on 1 and 8 DF,  p-value: 9.246e-06

Para o cenario 2, o valor do \(R^2\) é 0.92

Vamos analisar os residuos: