x1_m <- mean(df1.1$magic_score[df1.1$iden=="武装直升机"])
x2_m <- mean(df1.1$magic_score[df1.1$iden=="某品牌塑料袋"])
x_s <- sd(df1.1$magic_score)
N <- 100
r_pbis <- (x1_m-x2_m)/x_s*sqrt((N/2)*(N/2)/(N*(N-1)))
r_pbis[1] -0.6108072相信大家对盲人摸象的典故都不陌生。几个盲人接了个盲人按摩的活,给一头大象做马杀鸡1。每位盲人负责一个区域,有人摸腿,有人摸鼻子,有人摸肚子等等。最后活干完了,大家吵起来了,对自己摸的是啥产生了一些人民内部矛盾。
有趣的是,英语里还有个说法叫房间里的大象(elephant in the room),意指一个大家避免讨论但非常明显的问题。
在上一章中,我们已经通过独立样本t检验找到了一只大象——机人和袋人的魔法天赋有差异。从摸大象的角度看,我们已经睁着眼睛通过摸鼻子的方式摸出了这是一只大象。在这一章中,我希望带着各位读者以一种近似性骚扰的方式从各种角度重新摸,来展示我们能用多少种方式摸出这是一只大象。
描述数据的方式有非常多种。上面我们介绍的是针对数据集中趋势的统计检验。还有一个大家非常熟悉的描述统计方式,虽然可能很多人没有意识到这是一种描述统计,那就是相关。
相关字面意思地就是描述两个(当然也可以是多个)变量的关联程度。我们的大象——机人和袋人的魔法天赋不一样,可以从相关的角度去描述吗?当然没问题,用相关的语言,我们可以关注:一个人的魔法天赋是否与他是机人或者袋人有关?
所以这样一个相关中的两个变量是什么呢?一个是人的性别自我认同(机人 vs 袋人),另一个是魔法天赋分数。显然,前一个变量是一个只有两水平的类别变量,后一个变量是一个连续变量。统计学的好的读者肯定已经能脱口而出了,一个天然的二分类别变量和一个连续变量的相关应该使用点二列相关计算。
Equation eq-rb 就是点二列相关系数的计算公式。相关系数就是对于相关程度的数字描述,通常相关系数的取值范围是-1 ~ +1。 +1表示完全的正相关;-1表示完全的负相关;0表示两个变量没有关系。
我知道大家已经迫不及待想享受计算的乐趣了,让我们把我们的数据代入公式,开始计算吧。
x1_m <- mean(df1.1$magic_score[df1.1$iden=="武装直升机"])
x2_m <- mean(df1.1$magic_score[df1.1$iden=="某品牌塑料袋"])
x_s <- sd(df1.1$magic_score)
N <- 100
r_pbis <- (x1_m-x2_m)/x_s*sqrt((N/2)*(N/2)/(N*(N-1)))
r_pbis[1] -0.6108072计算的结果是,性别自我认同和魔法天赋分数的点二列相关系数是-0.61,这是一个相对比较高的相关系数。也在一定程度上说明了性别自我认同和魔法天赋分数存在关联。但是,还是像我们在第二章的时候讨论的问题,平均数有差异,那你怎么判断总体是不是真的有差异呢?同样的,我们算出了样本中的两变量相关,那么怎么知道总体中两个变量是否相关呢?
答案仍然是使用NHST,设定我们的零假设(r=0),然后构造抽样分布,得到样本中相关系数在抽样分布中的出现概率,通过alpha水平判断是否拒绝零假设。相关系数的抽样分布仍然可以使用t分布,有如下公式 Equation eq-tb :
我们又可以享受计算的乐趣了。
## 代入公式得到t值
t_pbis <- r_pbis*sqrt((N-2)/(1-r_pbis^2))
## 根据t值和自由度计算p值;乘以2计算双尾概率
p_pbis <- 2*(1- pt(abs(t_pbis), df=N-2))
## 输出结果
print(paste("点二列相关的双尾检验: r=", round(r_pbis, 4),",t=",round(t_pbis, 4),",p=",round(p_pbis, 15),",df=",N-2))[1] "点二列相关的双尾检验: r= -0.6108 ,t= -7.6368 ,p= 1.498e-11 ,df= 98"点二列相关系数的显著性检验说明,人们的自我性别认同和他们的魔法天赋分数之间的相关是显著的。这点也与我们的期待一致,毕竟大象就在房间里。不过,读者可以仔细检查一下我们上面做出的检验的具体数值,再对照上一章 sec-t检验实战 看看有没有什么发现?
是的,不管是t的绝对值,p值还是df值,针对这两个变量的点二列相关的显著性检验结果,和我们的独立样本t检验结果一模一样,一个数字都不带差的。为什么呢?
事实上,如果你将上面的点二列相关系数公式 Equation eq-rb 代入对其显著性进行检验的t检验公式 Equation eq-tb 中,最终可以得到下面的独立t检验公式。
这个推导十分简单,感兴趣的读者可以自己找一张草稿纸代入计算,并以此入眠。“可惜此处的空白太小”2,我就不详细推导了。读者只需要注意,N=n0 + n1 即可。
所以,换句话说,对于性别自我认同和魔法天赋分数这两个变量的点二列相关推论统计,跟比较机人和袋人的魔法天赋平均分数差异的推论统计,实际上是同一个东西。我们确实在摸同一只大象!
如果读者们系统学习过相关的统计知识3,应该会知道,点二列相关可以被看做是皮尔逊(Pearson)相关的特例。当然,我相信有一部分读者可能没有学过相关的概念,或更可能已经忘了皮尔逊相关是什么。简单地来说,皮尔逊相关主要用于描述两个连续变量之间相关关系。皮尔逊相关系数的计算公式如下:
事实上,当你用1和0分别表示机人和袋人,代入上面的公式中就可以得到我们的点二列相关系数公式 Equation eq-rb 。所以同样的,我们在我们的数据中也可以尝试使用1和0代表机人和袋人来进行一次相关系数检验。
## 分别用1和0表示机人和袋人
df1.1$iden_n <- c(rep(0,50),rep(1,50))
## 比较一下两个变量的差异
## 原来的变量
table(df1.1$iden)
某品牌塑料袋 武装直升机
50 50 ## 新生成的变量
table(df1.1$iden_n)
0 1
50 50 当然,你也可以使用as.numeric()命令直接改变iden变量的属性。但因为我被外星人劫持了,如果我不这么写代码的话他们就会把全世界的薯片都变成酸甜的番茄口味。为了全世界人类的福祉,我决定向外星人屈服。
好,现在我们有了一个新的性别自我认同变量(数字版)。我们就可以用它来算一个皮尔逊相关,并检验相关系数的显著性了。
cor.test(df1.1$iden_n,df1.1$magic_score)
Pearson's product-moment correlation
data: df1.1$iden_n and df1.1$magic_score
t = 7.6368, df = 98, p-value = 1.498e-11
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.4708826 0.7207539
sample estimates:
cor
0.6108072 结果如上,是的,我们又摸了大象一把。不过这次我们胸有成竹,因为我们已经知道本质就是同一个公式,那么结果自然也会一样。我猜,在你再次看到7.6368,1.498e-11这些数字时,已经无动于衷了。
不过当我们放到皮尔逊相关这个角度去摸这只大象时,不妨回忆一下,如果我们坐在统计的课堂上,当老师讲解这个概念时,使用的例子是什么样的。比如下面这个图,使用的就是鸢尾花的数据,呈现了花瓣长度(x轴)和花瓣宽度(y轴)之间的关系。见过花的读者应该都知道,这两个变量之间显然存在关系,在同一个物种上,花瓣不能光横着长或者竖着长。就好像在ppt里缩放图片,显然你得按住shift缩放才能保住花的真实感。所以,花的长度越长,一般宽度就越宽,反过来也一样。
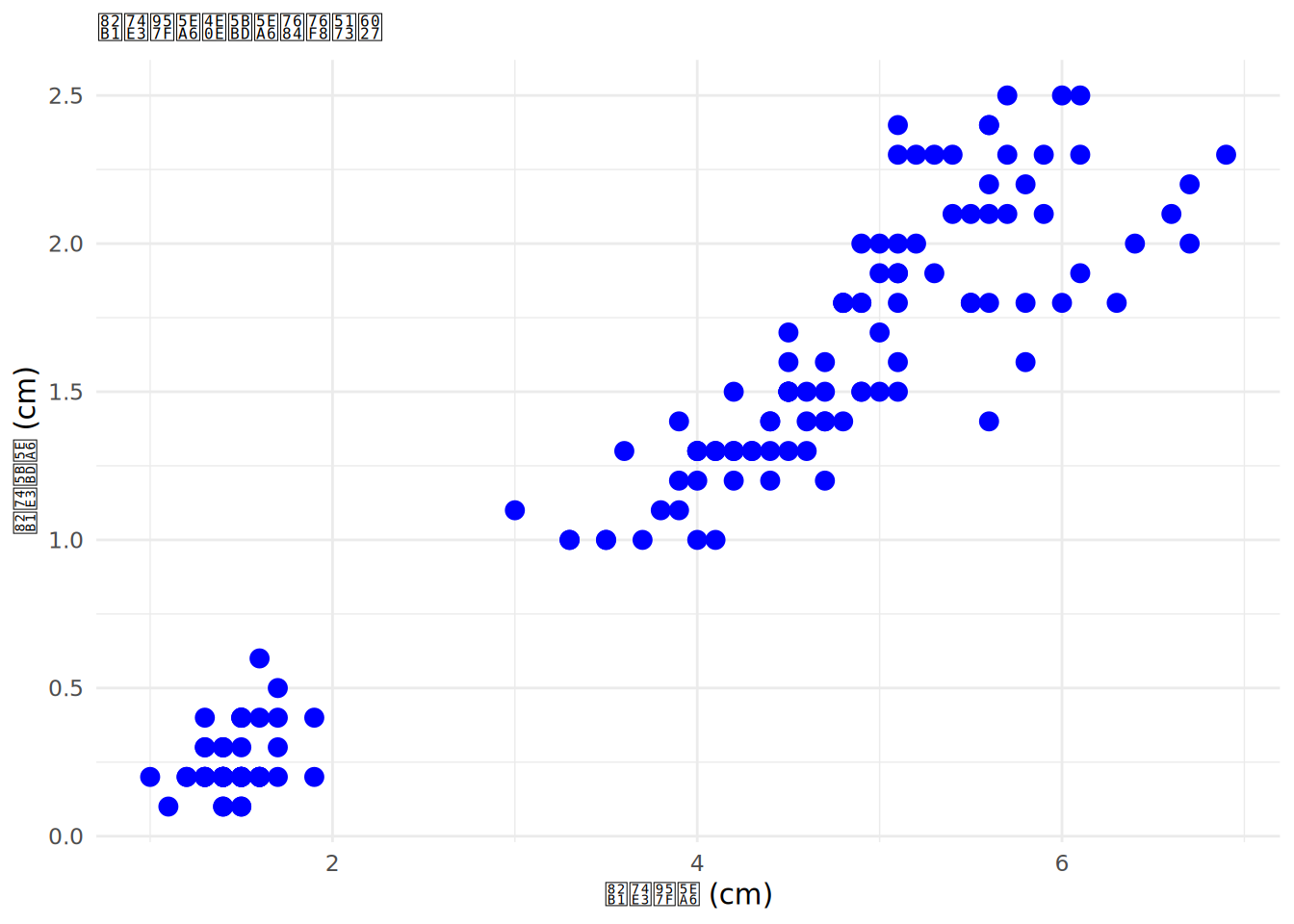
通常我们使用皮尔逊相关描述的就是这样两个连续变量之间的相关关系。从上面这张散点图来看,显然所有点都聚集在一起形成了一种趋势。这个趋势是什么呢,好难猜啊。
`geom_smooth()` using formula = 'y ~ x'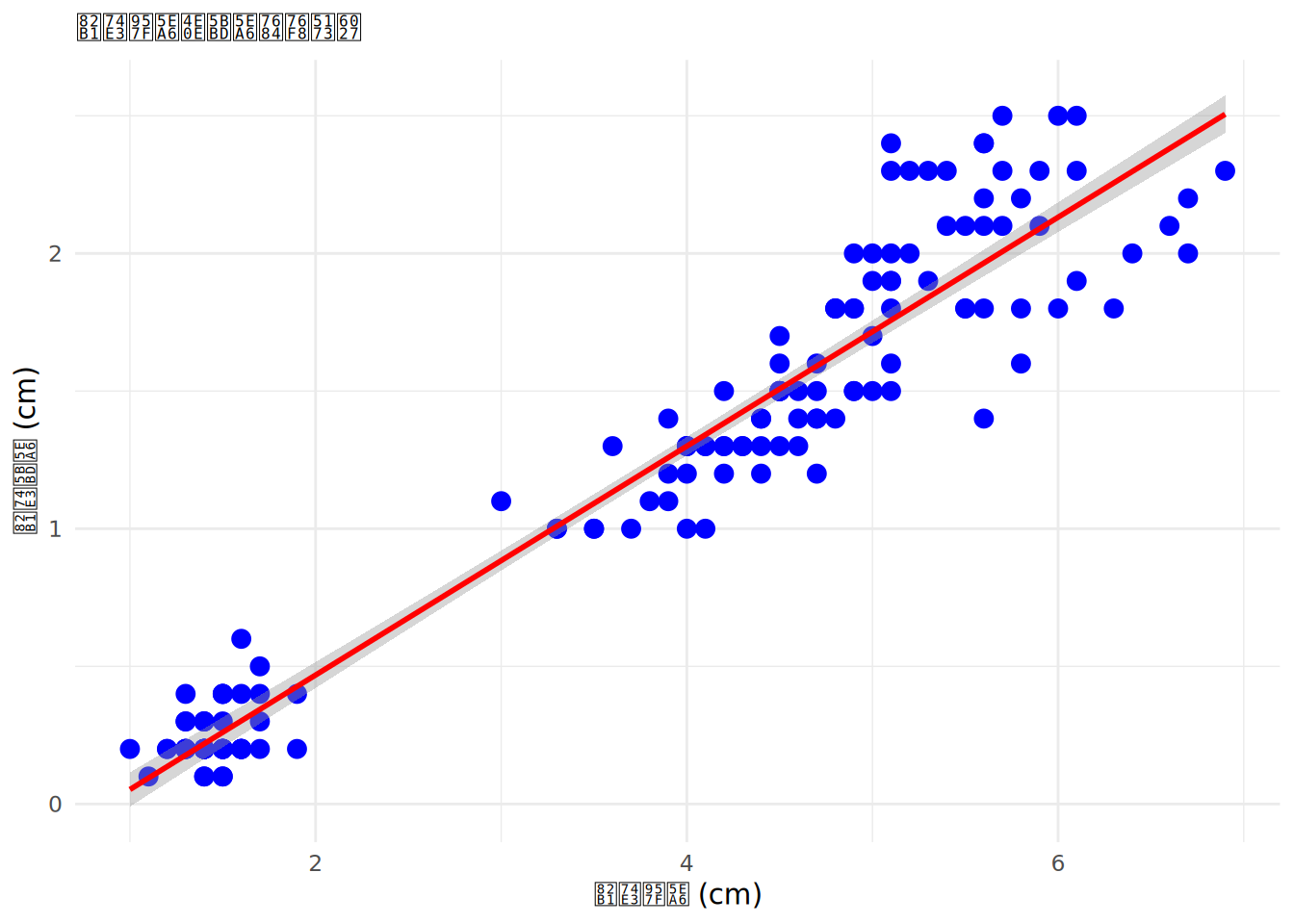
好了不卖关子了,相信很多读者都能直接画出上面图里的红线。这也是许多情况下对相关进行表征的一个办法。散点图里,显然蓝色的点似乎聚集在一条看不见的线附近,而我们心中的相关关系,很多时候都是这样一条的直线。
事实上,两变量的皮尔逊相关系数描述的就是两个变量的线性关系。比如下图中就展示了两个变量的散点图,如果对数据计算皮尔逊相关系数并检验显著性,r = -.052, p = .245。换句话说,皮尔逊相关的结果说明两个变量之间没有相关。图中拟合出的直线也似乎没有很好的描述数据的趋势。
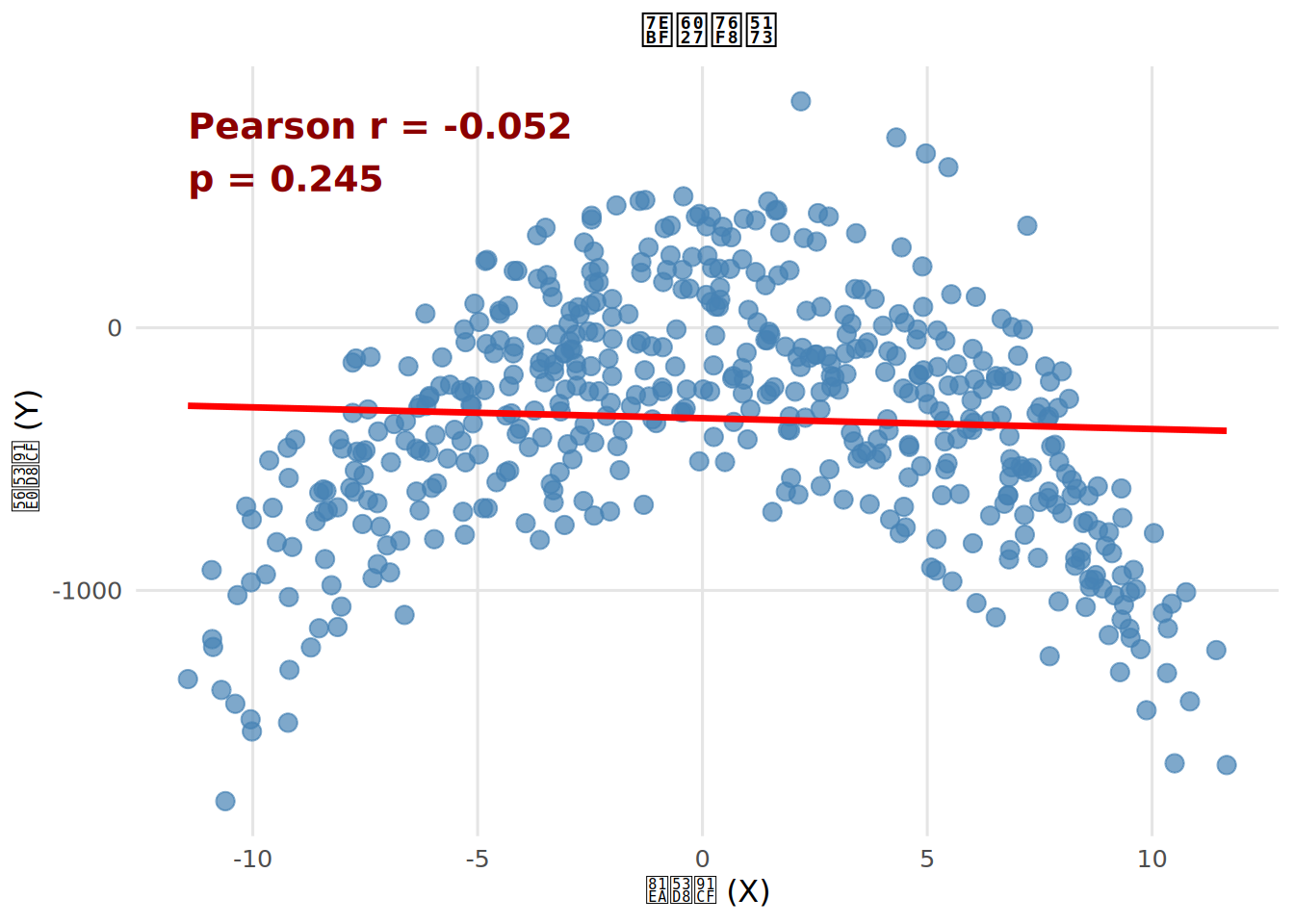
那么真实情况是什么样的呢。我们再看一张图。
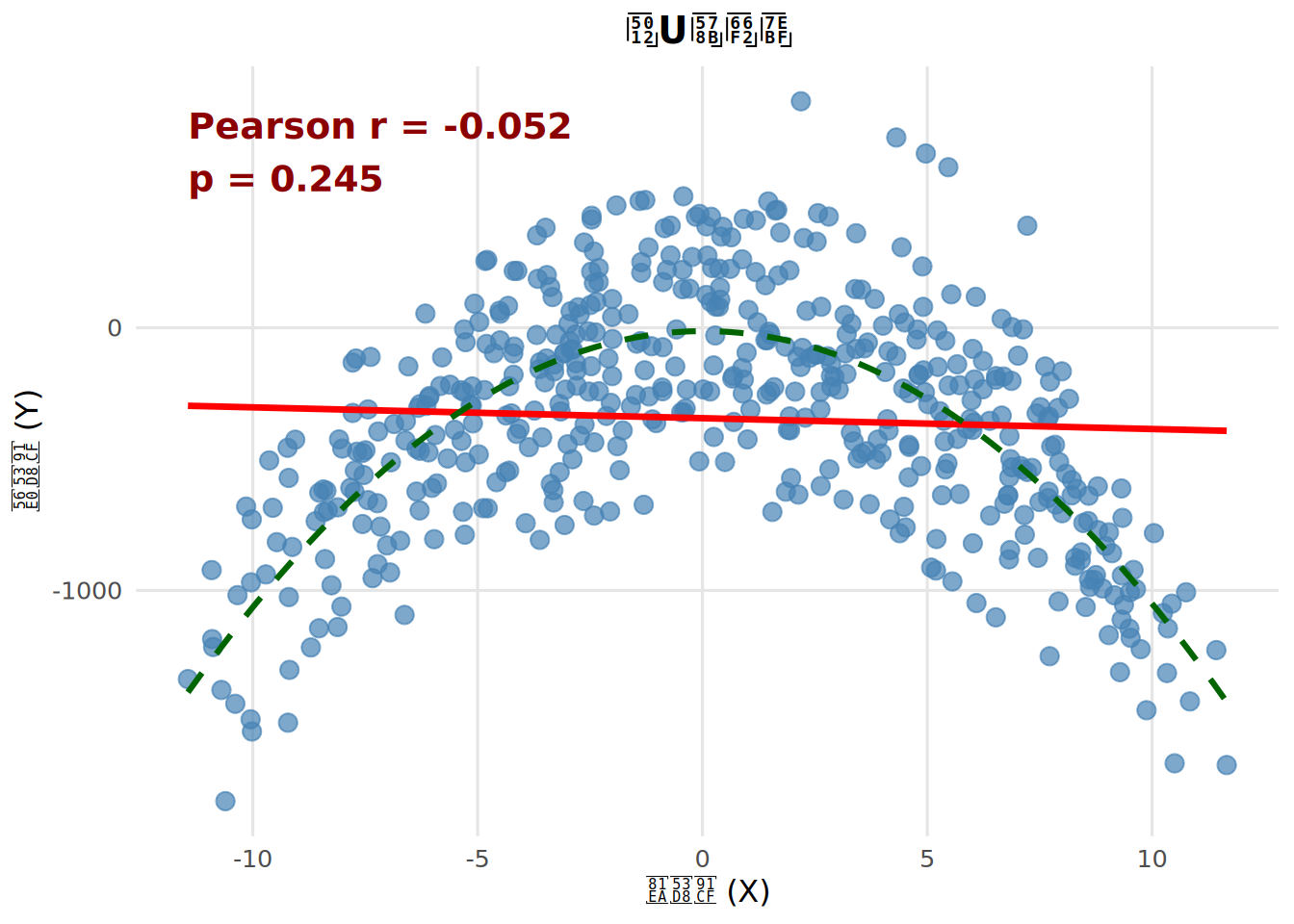
可以看到,图中的绿色虚线提示了两个变量间的关系其实是非线性的,实际上是一个倒U型曲线(想想心理学常说的关于动机和表现的耶基斯–多德森定律)。这条线一画,看上去就对数据的趋势有了一个贴切的描述。换句话说就是,皮尔逊相关系数并不能找到非线性,也就是不能用一条直线描述的相关关系(对非线性关系的检验我们会在 sec-nonlinear 中介绍)。所以,不管是点二项相关还是皮尔逊相关系数,反映的都是一种“线性”的相关关系。
那么,我们之前描述的关于性别自我认同和魔法天赋之间的关系,也可以在图里画上这样一条直线表示它们之间的关系。
我们在第一摸里花了那么久的时间,得到了两个结论。其一是,我们之前做的独立样本t检验,和自变量与因变量的相关系数显著性检验本质是一回事。另一个是,相关系数本质描述的,是一种线性关系。我们还把这种关系在之前的描述统计图里,用一条直线表示了出来。不知道读者有没有好奇,这条直线是怎么画出来的?
画这样一条直线,我们使用的是另一个统计工具,线性回归。这条直线就是所谓的回归直线。这个回归模型,可以写成一个一元一次方程:
所以我们管这样的模型叫做一元回归模型,因为这是最简单的线性回归模型,所以也叫简单线性回归。
咱们的九年义务教育还没忘的读者应该都能理解这样一个方程如何在直角坐标系中画出来。问题在于,我们如何确定b0 和b1 这两个系数。不过故事可能是完全反过来的。我们确定这两个系数的方法叫做最小二乘法,这个办法其实也简单地在笔者本人的高中数学里讲过。这个办法也叫最小平方法,也就是找到一个函数,让误差最小。误差是什么呢,就是函数对数据的预测与实际数据之间的差值。请看下图:
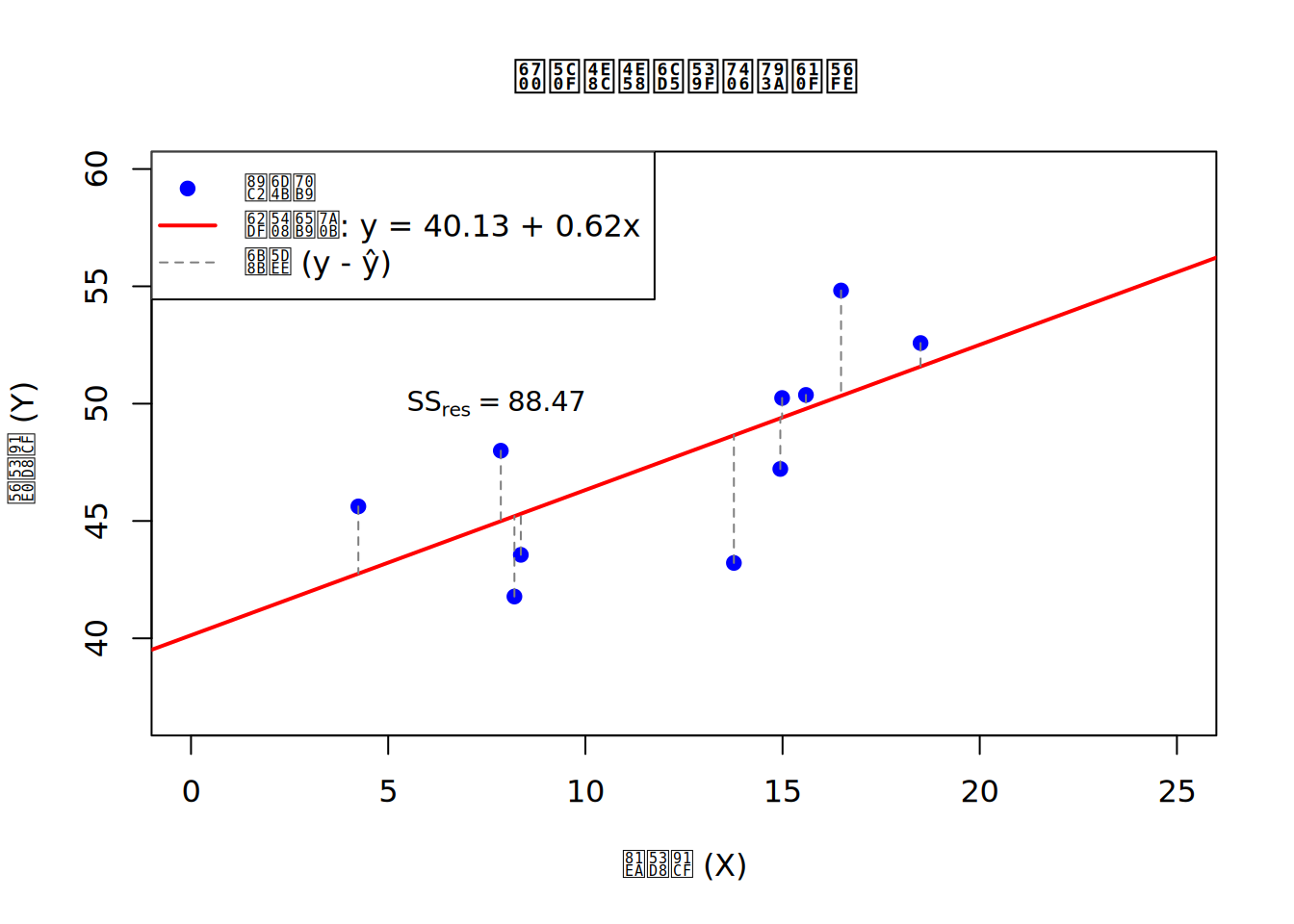
这条红线就是我们的函数(方程)。每个蓝点都是一个实际数据。可以看到,其实每个蓝点都没有在红线上,但可以从蓝点画一条垂直于x轴的线,连到红线上。这个线段就是误差。当然在计算上直接使用差值会有正负号不好加减的问题,所以我们可以把这个差值开平方以后相加,当这个平方和最小的时候(所以叫最小平方法),也就是每个点到线的距离之和最短的时候,就是对数据最佳的(线性)拟合。
如果对于任意一个原始数据点的坐标,那么对应的回归模型预测值是,误差就是。我们的方程也可以写成。简而言之,最小二乘法就是找到让e2最小的那个方程。
接下来我们来拟合一个能描述我们机人和袋人魔法天赋分数的线性回归模型。就像我们在独立样本t检验中做的那样,性别自我认同作为我们的预测变量,魔法天赋分数作为我们的结果变量。也就是我们一定程度上能通过一个人是机人还是袋人,判断ta的魔法天赋情况。
lm1 <- lm(magic_score~iden_n, df1.1)
summary(lm1)
Call:
lm(formula = magic_score ~ iden_n, data = df1.1)
Residuals:
Min 1Q Median 3Q Max
-18.414 -6.369 -1.198 6.157 25.225
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 81.240 1.301 62.426 < 2e-16 ***
iden_n 14.055 1.840 7.637 1.5e-11 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 9.202 on 98 degrees of freedom
Multiple R-squared: 0.3731, Adjusted R-squared: 0.3667
F-statistic: 58.32 on 1 and 98 DF, p-value: 1.498e-11上面就是我们的回归分析的统计结果。运用最小二乘法拟合数据找到的回归方程是。换言之b0=81.240,b1=14.055。如果你还残存着高中的数学知识,应该还记得,我们把b0叫做截距,b1叫做斜率。不过,这两个系数有什么实际意义吗?
不知道读者们还记不记得我们之前的几个关键数值,比如“点二列相关的双尾检验: r= -0.6108 ,t= -7.6368 ,p= 1.498e-11 ,df= 98”。再拿着这些数值回到我们回归方程的拟合结果逡巡一下,就会发现,咦,怎么对于预测变量的斜率进行的显著性检验,结果还是一样的?换句话说,就像相关系数一样,斜率作为一个描述统计的数值,它跟零之间的差异的显著性检验,也是在检验机人和袋人的魔法天赋是否有差异,也是在检验自我性别认同和魔法天赋之间是否相关。是的,我们又摸了大象一把。
原理是什么呢?我们不妨回到上面的图,不过我们可以在图里再画两条辅助线。
上图还是我们对于数据的描述性统计。两个红色三角形,对应的分别是两个人群的平均魔法天赋,分别是81.2395(机人),和95.29439(袋人)。还记得回归方程是如何得出的吗?最小二乘法,找到误差最小的那条线。在这个回归模型里,我们的机人对应的还是皮尔逊相关里使用的0,袋人对应1。那么,对于机人来说,也就是x=0,距离所有实际数据y误差最小的那个点是多少呢?
没错,就是它们的平均数。同理,袋人也是一样的。
那么,我们把这两个点一连线,画出来的就是对应的回归线。所以b0=81.240对应的是什么呢?x=0时函数预测的y值,这个值就是机人的平均魔法天赋分数。斜率b1又对应着什么呢?如果你们还记得斜率的几何意义,应该能看出来,斜率对应的就是图中紫色的虚线除以绿色的虚线(也就是蓝线与绿虚线夹角的tan值)。紫色的虚线是什么呢?机人与袋人魔法天赋平均数之差。绿色虚线是什么呢?机人与袋人对应的x值之差。斜率其实就是在反映预测变量x每一个单位的增长,会导致y增加多少。转化成数学形式:
还记得我们对机人和袋人赋的x值吗?对,0和1。所以上面那个式子的分母就是1,斜率b1就是机人和袋人的魔法天赋分数的差值。检验它是否显著,就是在检验机人和袋人的平均魔法天赋分数的差异是否显著!
我们还可以做一件事,把两个变量都做标准化处理,转变为Z分数,也就是标准分数。忘了这是什么东西的读者可以回到第二章@sec-零假设显著性检验 的部分,在其中我们介绍正态分布的时候提到了Z分数。
lm1 <- lm(scale(magic_score)~scale(iden_n), df1.1)
summary(lm1)
Call:
lm(formula = scale(magic_score) ~ scale(iden_n), data = df1.1)
Residuals:
Min 1Q Median 3Q Max
-1.5925 -0.5508 -0.1036 0.5325 2.1815
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -5.092e-16 7.958e-02 0.000 1
scale(iden_n) 6.108e-01 7.998e-02 7.637 1.5e-11 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.7958 on 98 degrees of freedom
Multiple R-squared: 0.3731, Adjusted R-squared: 0.3667
F-statistic: 58.32 on 1 and 98 DF, p-value: 1.498e-11以上就是把两个变量标准化之后的结果。可以看出,标准化之后,回归方程的截距实际上变成了零4。而斜率的显著性检验结果,仍然和上面使用原始分数计算的一样。换句话说,标准化并不改变数据的显著性。 不过更重要的是,不知道大家有没有注意到标准化后斜率的数值。还记得我们的相关系数的值吗?
r_pbis[1] -0.6108072是的,这个斜率就是两个变量的相关系数!
其实,考虑到用最小二乘法生成的回归模型,其中斜率的计算公式就是 回到皮尔逊相关系数的计算公式 Equation eq-rp 观察,其实 回归系数和相关系数仅在分母上有所差别。即 所以,当你把两个变量转换成分布形态一样,但平均数为0,标准差为1的标准正态分布时,两个变量的标准差在上面的公式中就都变为1,斜率就跟相关系数相等了。 事实上,不管是 Equation eq-as 还是 Equation eq-rs 的显著性检验,都是在把它们跟0比较。那么它们是否等于0,取决于分子是否为零。而我们构造出的这些式子,最终指向的结果是,在这样一个两水平的分类变量作为自变量的情况下,斜率是否为0,取决于平均数之差是否为零或相关是否为零。根本而言,这都是我们伸向大象的黑手,走了不同的路径而已。
在这第二摸的最后,我们可以总结一下,不管是处理平均数差异的独立样本t检验,还是关心两变量关系的相关系数,或者是反映结果变量随预测变量变化而变化的斜率,本质上对它们的显著性检验都是在检验同一只大象。而本书的一大目标,就是用回归模型带你重走取经路,看看你之前学过的各种检验如何在线性模型中理解,并把它作为一种工具,灵活地运用于你遇到的更加复杂的统计问题之中。
是的,在第一章中,我说我们要放弃直线,走一段弯路。这段弯路,就是让我们运用“直线”——以线性关系来统合你之前学过的心理统计。很有意思的转折,不是吗?
也许摸完第二摸之后,读者也许会觉得,这大象都快被你摸秃了,你还要摸吗?是的,我们已经在第二摸中引出了本书的中心主题。但心理统计本科阶段的最后一块拼图并没有拼上,那就是大家最熟悉又陌生的——方差分析。
方差分析的原理是什么呢?还记得我们的假设是什么吗?
在上一章t检验的介绍( sec-tdis )里,我们使用t检验直接对是否等于0做检验。这实际上采用的是一种直接针对集中趋势(平均数)差异的检验方式。第一摸中,我们针对的是另一个常见的描述统计指标——相关做了显著性的假设检验。那么,我们还有什么常见的描述统计没有用过吗?
是的,方差分析的方差。因为我们使用的是样本,所以使用样本数据估计总体方差的公式是:
这里的n-1,实际上是自由度(degree of freedom, df),即在这里,df=n-1。我们其实在上一章中触碰过自由度的概念,但是并没有展开来讲。聪明的读者能回忆起来是在那里讲的吗?是的,还是在t检验,我们介绍t分布的形态会随着自由度的改变而改变。之后我们介绍了独立样本t检验的公式 Equation eq-tee ,z在它下面还有一个对于方差的公式。我们再来看一下:
和 分别对应机人和袋人的方差。观察这个公式你可以发现,其实公式的分子就是机人和袋人两个方差公式的分子相加,因为这就是样本方差乘以对应样本的自由度;而分母对应的就是两个样本对应的自由度相加。
上面的公式实际上就是试图把机人和袋人的方差根据他们的样本量(或者说,自由度)重新加权生成一个能表示把他们放在一起时(pooled)的方差情况。所以观察 Equation eq-ssq 以及 Equation eq-spp 可以发现,其实方差的基本形式就是分子是原始分数减去它们的平均数的平方和,我们叫它离均差平方和。在统计里,我们一般认为这个统计量代表着一组数据的变异(variation)。这一部分是可以进行加减计算的,像 Equation eq-spp 这样。
那么分母就更好理解了,就是这组变异所对应的自由度。不过自由度这个概念相对就比较抽象了。不知道我上面在介绍样本方差的公式 Equation eq-ssq 时有没有读者奇怪,为什么分母除的不是n而是n-1呢?其实如果这组数据不是来自样本而是总体,那么总体方差的公式确实应该是n。如果读者们之前学过统计的知识,比如我前两天刚刚监考过我校数理统计与概率论的课程期末考试,试卷里好几题都在测试学生们对于样本方差的分母应该使用自由度,这样才是对总体方差的无偏估计这一概念5。所以,实际上我们一般只在使用样本估计总体时使用自由度这个概念。
通常在统计概念上,自由度顾名思义,指的是样本数据中能自由变化的个数。肯定有读者好奇过,同样都是对总体数据进行估计,为什么对总体平均数的无偏估计就不需要除以df呢?即
其实我们也可以把计算样本平均数的公式写成这种形式。问题在于,在计算样本平均数时,数据中能自由变化的个数是多少呢?举个例子:
计算这样一组样本数据的和,比如袋人的样本,每个样本数据Y都可以自由变化。所以这里的df就等于样本容量n。
我们再看我们的样本方差的公式 Equation eq-ssq 呢。只看分子:
这样一组离均差平方和每个 是否都是可以自由变化的呢?并不是,因为在这个数据中,还使用了一个统计量,而这个平均数是在使用原始数据Y减去它的时候就已经确定了的。换句话说,每个 中的Y,都已经提前被用于计算 了。那么在上面的公式 Equation eq-ss 中,能自由变化的Y有多少个呢?
我们可以这么思考,先假设排在公式前面的几个Y都在自由变化,那么到第几个的时候它就不得不被前面几个兄弟拖累,只能配合它们演出而尽力在表演了呢?平均数的公式是这个,也就是上面求和公式再除以样本量(或者自由度):
n显然是一个常数,所以通常统计上平均数和求和本质上是一个东西6。对于 Equation eq-ss 来说, 已经确定了。那么当Y在其中自由变化时,变化到 时, 就会尴尬地发现,因为 已经确定,所以它就得是那个配合演出的倒霉蛋了。比如一个六个袋人的样本平均魔法天赋是2,前五个自由变化的袋人最后整出了个200的平均数,那最后一个袋人只能含泪认下自己不能再自由变了,只能是(2*6-200*5)=-988 这么屈辱的分数。所以,在计算样本方差时,自由度是n-1,因为第n个哥们儿为了平均数固定不得不为前面n-1个兄弟的自由飞翔买单。 这时候,我们再回头看 Equation eq-spp 这个公式。自由度为什么-2也就好理解了,因为我们在计算分子平方和时,使用了两个样本平均数,所以两个样本都有一个哥们得买单。而这个公式也揭示了,对于多个样本的方差计算,可以分别计算几个离均差平方和(或者说变异)相加,再除以几个平方和对应的自由度。
换句话说,样本方差本质就是反映一组数据的变异平均分到每个能自由变化的个体上会是多少。就像总体方差是反映总体变异平均给总体的每个个体会是多少一样。
我们之前提到一个新思路,除了直接通过平均数的抽样分布比较集中趋势也就是平均数差异的显著性(独立样本t检验)之外,是不是可以通过离中趋势也就是方差的比较来看两个样本是否有差异呢。上面对于方差公式的分析说明,公式中的分子,也就是离均差平方和,或者说变异,是可以加减后再除以自由度计算“方差”的。换句话说,我们可以把一个样本中的离中趋势,或者说变异,分解成几个不同的部分。那么,问题就变成了,怎么分解这些变异呢?
回到我们的数据,我们可以计算几个方差?这个问题相信大家不难回答。样本中的机人和袋人合在一起作为一个大样本,可以计算他们的魔法天赋样本方差。如下图,估计所有个体距离所有个体的平均数的差异。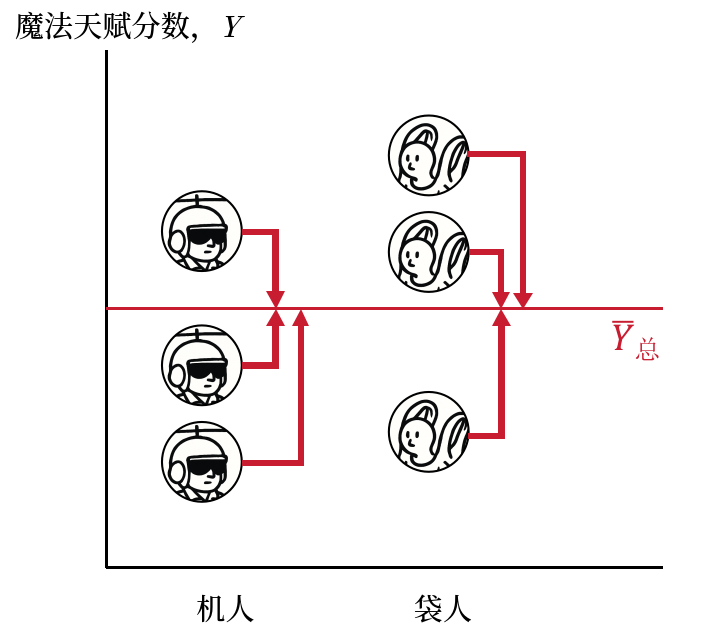
机人自己作为一个样本有一个样本方差,袋人同理,对应的公式还是使用 Equation eq-ssq 就不再重复了。如下图,两个样本中的个体,分别计算他们与对应的样本平均数的差异,即机人算一个方差,袋人算一个方差。
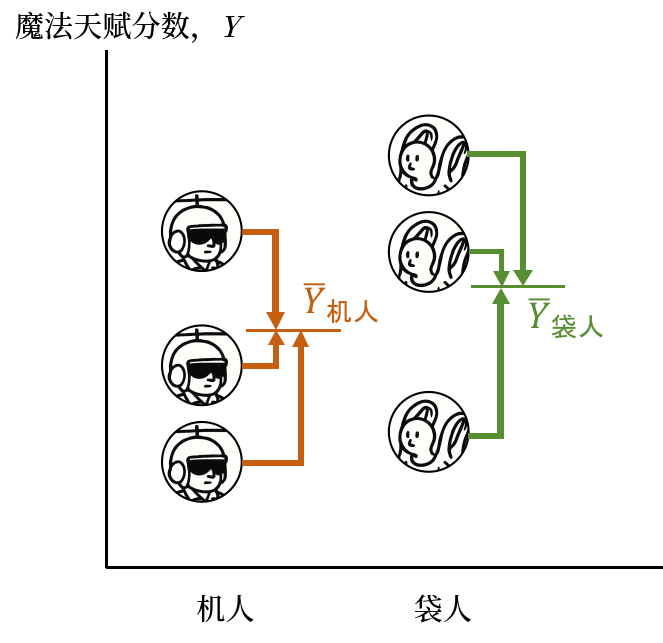
还有一个大家可能会忽略的,是用机人和袋人的魔法天赋平均数,分别代表这两个样本中所有个体的魔法天赋情况7,进而计算这样两个由平均数组成样本与两个样本中所有个体的平均数之间的平均数。为了方便大家理解,下面写出它的计算公式:
就像 Equation eq-spp 的形式一样,实际上这也是一个对于两样本方差的加权平均,只不过这两个样本是样本的平均数而不是原始值。如下图,所有的机人个体用机人平均数代替计算他们到机人袋人合在一起后的平均数差异;袋人个体用袋人的平均数代替。
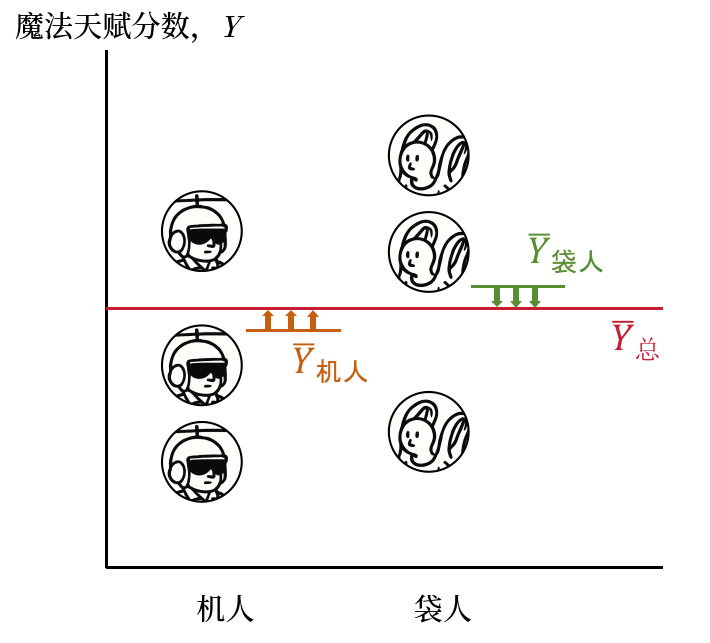
那么为了进行加减运算,我们可以提取这几个方差的分子,也就是我们之前提到的离均差平方和,在方差分析中,我们用SS(Sum of squares)来表示。两个样本中所有个体合在一起的魔法天赋的离均差平方和,我们称为SStotal ,简写为SST。
sst <- var(df1.1$magic_score)*99机人样本的方差的分子,即机人样本的魔法天赋平方和,SS机人,因为代码里不方便写中文,我们记作SS0,也就是我们之前给它的赋值。
ss0 <- var(df1.1[df1.1$iden_n==0,"magic_score"])*49同理,袋人的魔法天赋平方和,SS袋人 。记作SS1。
ss1 <- var(df1.1[df1.1$iden_n==1,"magic_score"])*49这两个样本的平方和相加,就是两个组的组内平方和,记作SSwithin ,简写为SSW。
ssw <- ss0 + ss1Equation eq-ssb 计算的两组人平均数之间的平方和,SSbetween ,简写为SSB。
## 机人的魔法天赋平均数
mach_man_m <- mean(df1.1[df1.1$iden_n==0,"magic_score"])
## 袋人的魔法天赋平均数
bag_man_m <- mean(df1.1[df1.1$iden_n==1,"magic_score"])
## 总平均数
grand_m <- mean(df1.1[,"magic_score"])
ssb <- ((mach_man_m-grand_m)^2*50 + (bag_man_m-grand_m)^2*50)*1我们把这几个数放在一起看看。
sst[1] 13236.86ssw[1] 8298.377ssb[1] 4938.478不知道对数字敏感的读者有没有发现什么?
sst[1] 13236.86ssw+ssb[1] 13236.86是的SST=SSW+SSB。机人和袋人这两个组的总体平方和可以被分解,或者说拆成两个部分:(1)SSW:两个组分别计算组内个体与组平均数差异的平方和之和,即组内平方和;(2)SSB:用组平均数代表组内的每个个体,计算他们到这两组合起来以后总平均数的差异平方和,即组间平方和。好吧,我知道这两句话很拗口,但没关系,你可以翻到前面看看公式和图配合理解。
现在的关键是,为什么SST=SSW+SSB呢?
回想一下,我们在第二章中讨论过,当你抽取了一个样本的魔法天赋分数,如果有人要你报告这个样本的情况,你会怎么报告呢?用平均数对吧?所以对于我们的数据,机人和袋人两个组合在一起,对于他们魔法天赋的描述,我们也用他们合在一起的平均数表示。也就是我们上面几幅图中的。
那么,当我们用变异的角度来看, 描述了两个组所有个体的魔法天赋情况,那么所有个体偏离这个平均数的情况,就是他们“不受拘束”“肆意妄为”的所有变异,也就是我们计算的SST。
那么,我们的假设是什么呢?我们认为,这么一大群人,实际上有一个有意义的划分,就是机人和袋人。换句话说,在形成魔法天赋的过程中,你是机人或者是袋人,会影响你的魔法天赋分数。那么你作为一个机人或者袋人,对魔法天赋分数的影响,是不是也体现在偏离的变异中呢?显然是的。那么这部分我们用机人和袋人解释的变异体现为什么呢?当然是机人的平均数和袋人的平均数,分别偏离的那部分,也就是SSB。
好的,那么我们就剩下了SSW。SSW是什么呢?机人和袋人内部,每个个体偏离组平均魔法天赋的变异。换句话说,就是当你是机人或者袋人,你也必然会有一些跟你相同性别自我认同的人不一样的魔法天赋,毕竟显然魔法天赋不可能完全由你的性别自我认同决定。这部分的变异,不是由机人或者袋人导致的,也就是总变异中,不能被性别自我认同解释的部分。
现在,你可以理解了吗?
SST(总变异)=SSB(组间变异:用机人和袋人解释的变异)+SSW(组内变异:机人和袋人不能解释的变异)
就像我们一般不拿机人和袋人两个组的魔法天赋总和进行比较,而是计算一个人均魔法天赋分数进行比较一样;通常我们也不用离均差平方和也就是SS进行比较,而是计算平均每个自由度的“变异”,其实也就是“方差”,大家可以再回去看看公式 Equation eq-ssq 。 我们在方差分析中把这种“平均”后的的离均差平方和叫做,均方(Mean Square, MS),挺顾名思义的对吧。
所以,我们现在可以计算出三个均方,MST= SST/dfT; MSB = SSB/dfB; MSW = SSW/dfW。MST其实就是一个样本对于总体方差的无偏估计。但更关键的是后面两个MSB和MSW。
就像我们上面分析的MSB对应的组间变异代表的是,由性别自我认同,也就是机人和袋人带来的平均数离开的变异。这部分变异其实描述的是我们提出的假设——性别自我认同影响魔法天赋。而MSW对应的组内变异,代表的是不由性别自我认同假设解释的变异。
而这两种变异,在经过“平均化”,变成均方后,都像MST一样,也可以视为一种对于总体方差的估计。
那么,再回想一下我们在进行t检验的时候所使用的零假设:
如果这个假设成立,说明性别自我认同带来的变异对应的MSB是随机的,这种随机效应也是不由性别自我认同假设解释的变异,本质上,这部分的变异来源就跟MSW的来源是一致的,都是作用在个体上的随机的(其他)效应带来的。换句话说,机人袋人内部跟他们的组平均魔法天赋不一样的差异,我们认为就是像扔骰子一样随机出现的。那么如果机人和袋人这个划分其实在总体上对魔法天赋没影响,那么在样本中表现出来的,他们各自的平均数和总平均数之间的差异,也是扔骰子扔出来的。
那么我们怎么推翻这个零假设呢?如果零假设不成立,意味着机人袋人的平均数和总平均数的差异不是扔骰子扔出来的。那么对应的MSB就应该比扔骰子扔出来的MSW更大。有聪明的读者可能会说,我懂了,那我们的零假设就可以是:
就像t检验一样,我们可以这么转换一下:
然后计算左边的显著性。
不过可惜的是,方差或者均方是不可以加减的,还记得我们上面在做什么吗?我们在加减计算的都是离均差平方和,而不是均方。而离均差平方和因为没有平均化又不能用于比较。那咋办呢?
不卖关子了,统计学家发现,虽然均方之差我们可能没有简便的办法,但是均方相除的分布满足F分布。所以,我们的零假设就变成了:
那么,如果这个F值显著地大于1,那么就能推翻零@eq-MSB假设,验证我们地备择假设了。接下来地一切,就跟t检验在t分布中做的一样了。这就是方差分析。
接下来我们就可以进行方差分析了。下面是代码和结果,写法是不是跟回归分析的部分有些像?
aov1 <- aov(magic_score~iden, df1.1)
summary(aov1) Df Sum Sq Mean Sq F value Pr(>F)
iden 1 4938 4938 58.32 1.5e-11 ***
Residuals 98 8298 85
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1所以上面呈现了一个方差分析的输出结果,方差分析表。iden就是我们的自变量,也就是个体的性别自我认同,他是机人还是袋人,对应组间变异。Residuals 残差,也就是不能被解释的变异,对应组内变异。后面的几栏,df就是自由度想必大家都知道,Sum Sq就是SS 离均差平方和,Mean Sq就是MS 均方。F value就是F值,看看上面最后的零假设。Pr(>F) 就是我们朝思暮想的p值。
所以我们看到这个结果一般这么报告,机人和袋人的魔法天赋分数存在显著差异,F(1,98) = 58.32, p <.001.
好了,其实上面浪费了那么多篇幅,仅仅只是帮大家重温了一边方差分析的原理。相信有些读者直接快速扫过,直接看到了这里。显然,现在我们要开始展示,方差分析只不过是平平无奇的另一摸罢了。
首先我们还是回到方差分析的结果,有没有什么跟之前的分析一样的部分呢?
自由度df都是98,不是巧合。p值,跟之前的1.497*10-11比较,似乎也就是一个四舍五入的结果。
p_pbis[1] 1.497957e-11不过,我想提醒大家关注一下F值。回想一下,我们之前的t检验中,t值是多少呢?7.636829。发现什么了吗?
t_pbis[1] -7.636829还没发现,让我们把它平方一下,再看看?
t_pbis^2[1] 58.32115是的,F=t2。
我们回顾一下,F值是怎么计算的:Equation eq-F 。MSB是什么?Equation eq-MSB 。 MSW是什么?机人和袋人内部的离均差平方和之和除以自由度,前面没有专门写过。写在下面:
大家可以回第二章看看t值的公式 Equation eq-tee 。把t值公式平方之后,易证得 t2=F,此处略去过程8。
这说明F检验和t检验本质上是等价的,或者说,是摸的同一个大象。这点相信大家已经不意外了。不过,这从另一个角度揭示了,从集中趋势平均数比较出发,用平均数之差的分布作为显著性检验的t检验;和从离散趋势方差比较出发,用均方的比值的分布作为显著性检验的F检验,本质上是一回事。
要理解平均数差异和方差比较本质是一回事,我们不妨再回到回归模型中。还记得我们的回归方程吗?
在我们的数据里,机人对应iden=0,袋人对应iden=1。拟合后,b0是机人的组内平均魔法天赋分数,b1 是袋人和机人的组内平均魔法天赋分数之差。我们也把 这部分称为 ,表示根据拟合的回归方程计算出的对结果变量的预测值。显然,当iden=0时, ,也就是机人的魔法天赋均值;当iden=1时, ,也就是袋人的魔法天赋均值。所以,我们的回归模型本质也可以看作是原始数据=预测值+误差的形式:
所以回到我们机人和袋人的数据,我们可以用下面的表格进一步理解。每一行都代表一个个体,前50是机人,后50是袋人。
| 原始数据Y | b0 | b1*x | 预测值 | e |
|---|---|---|---|---|
| 0 | ||||
| 0 | ||||
| 0 | ||||
| 0 | ||||
| … | … | … | … | … |
| 0 | ||||
| … | … | … | … | … |
通过上面的表格,我们就可以更清晰的感受到,这个回归模型,本质就是使用机人和袋人的组均值,去预测每个个体的表现,剩下的就是预测的误差(残差)。所以我们上面的公式 Equation eq-lm1 ,可以理解为:
这样看上去就是一个基于均值预测数据的模型,对吧?接下来我们可以动一点小手术,把 Equation eq-lm1 改造一下:
上面的式子,在等号两边各减去了所有个体的平均数,然后把参照上面的表,把残差e用y和预测值表示,显然,等式依然成立。等等,这几个括号形式怎么有点眼熟呢?我们可以再把两边平方一下:
按照我们这么严谨的推导过程,这个式子显然对任意一个机人或袋人的个体都成立。那么,我们把样本中所有的机人和袋人求和,会得到什么呢?换句话说,就像上面的表格那样,把每一列中的所有单元格相加。只不过,现在的表格变成了:
| 原始数据Y | ||||
|---|---|---|---|---|
| … | … | … | … | |
| … | … | … | … | … |
| … | … | … | … |
求和的结果呢?
是不是更眼熟了?这不就是离均差平方和吗?我们上面说了,y的预测值其实就是机人和袋人的组均值,相信聪明的读者不难看出,上面的式子,其实就是:
那么后面这坨 是什么呢?我们分别考虑 和 的值。考虑到 9, 和 都等于0。读者可能要说,啊哈,被我抓到了,两个变量各自求和等于0可不一定它们的乘积求和也等于0。没错,不过我想要说明的是 和 ,也都等于0。它们是什么呢?对,就是平均数。所以我想构建的是下面这个式子:
如果我们把 和 看成两个变量X和Y,那么上面的式子可以看作是
而回到皮尔逊相关系数的计算公式 Equation eq-rp 以及Z分数的计算公式,不难看出,皮尔逊的相关系数公式也可以写成(这也是相关系数的另一个形式的公式):
实际上,皮尔逊相关系数的另一种写法是: 而当我们对原始数据进行标准化之后,两个变量的标准差都变成了1。换句话说,相关系数其实就是Cov,也就是协方差的标准分数。所以,协方差也在一定程度上反映了两个变量之间的相关程度,只不过它是非标准化的,也就是它的取值范围不在-1~+1之间,但正值仍然代表正相关,负值仍然代表负相关,0表示没有相关。
到这里你应该意识到了,我们上面费了半天劲推导 是什么。实际上它是 和 这两个变量协方差的分子。那么这两个变量的相关程度是怎么样的呢? 是预测值(组平均)减去一个常数(样本总平均数),而加减常数是不影响相关程度的。 是残差。而回归分析的一个基本假设就是,模型预测值(预测变量)和残差彼此独立,意思就是它们的相关为0。其实道理很简单,如果你的预测值和残差之间存在相关,那么说明你的预测变量没有被全部有效地用于预测结果变量,还剩了一点流到了残差里,这显然是不能接受的。
好了,这样我们历尽艰险,最终发现,从@eq-lm1 这样一个回归方程的均值角度出发,经过一系列的变换,最终可以得到我们在方差分析中使用的SST=SSB+SSW。均值和方差对应的统计检验,又一次找到了内在联系。
事实上,在我们论述到平方和的时候,不知道你有没有会想起,当我们在第二摸的时候提到,回归方程的拟合方法使用了最小二乘法,也叫最小平方法。回到我们在第二摸回归中使用的辅助图,你会发现,我们计算的,两组数据的平方和,不就是在回归中计算的所有数据到回归线(也就是预测数据——组平均数)的距离的平方吗?本质上,最小二乘法要找到的最小平方和,就是我们的SSW。通过最小二乘法分离出了SSW对应的残差,剩下的不就是回归模型解释的变异,在我们的数据里,对应的就是组平均值带来的SSB。
所以,对于回归模型来说,可以使用另一个角度的变异分解:
也就是,总变异=模型解释的变异+随机误差带来的变异。
来看看我们之前的回归分析结果:
lm1 <- lm(magic_score~iden_n, df1.1)
summary(lm1)
Call:
lm(formula = magic_score ~ iden_n, data = df1.1)
Residuals:
Min 1Q Median 3Q Max
-18.414 -6.369 -1.198 6.157 25.225
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 81.240 1.301 62.426 < 2e-16 ***
iden_n 14.055 1.840 7.637 1.5e-11 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 9.202 on 98 degrees of freedom
Multiple R-squared: 0.3731, Adjusted R-squared: 0.3667
F-statistic: 58.32 on 1 and 98 DF, p-value: 1.498e-11不知道大家在第二摸的时候有没有注意到这个结果的最后一行,F-statistic: 58.32 on 1 and 98 DF, p-value: 1.498e-11。是的,虽然我在上面绕了一个大圈子,但其实回归分析的结果里就已经明明白白地写着跟我们方差分析一模一样的结果。但是,为什么一个回归模型的结果输出,最后要报告一个方差分析的结果呢?答案还是要回到我们上面说的,回归模型中针对模型的变异分解上来。
其实这种把变异分解为模型和残差的视角不仅仅用于回归模型,大部分试图对实际数据进行拟合的模型都可以这么看待模型的表现情况,比如最近很流行的机器学习模型。换言之,包括回归模型在内的任何一个学习模型,我们都希望在理想情况下它能够更多地解释总体变异,尽量降低残差(也就是模型不能拟合的数据部分)。
那么很自然的,你就会想要通过变异构建一个指标来衡量模型的拟合情况。比如:
显然,这是一个比值,而且模型解释的变异永远不可能大于总变异,所以这是一个取值范围在0~1的指标。指标的值越大,说明模型解释的变异占总变异的比例越高,模型表现的越好。
ssb/sst[1] 0.3730855你能在回归分析的结果输出中找到这个指标吗?是的,就是Multiple R-squared,也就是R210。我们在回归分析结果输出中看到的最后一行方差分析的结果,就是在检验 R2即模型解释的变异在总变异中占的比例是否显著大于零,本质上还是在对解释的“平均”变异是否多于“误差”做检验,所以这个F检验其实就是:
对应我们的数据,因为我们的回归方程只有一个预测变量——自我性别认同,所以MSmodel 就是我们方差分析中使用的组间均方,MSerror 就是我们的误差均方。在我们这个回归模型上看,对于模型的R2的检验,就是对机人和袋人使用方差分析的检验。
了解了这个之后,其实给我们提供了看待心理统计或者统计模型本身的新视角。我们在心理研究中使用的任何统计模型,不管是t检验、F检验、回归分析或者你将来可能会接触到的逻辑回归、机器学习模型等等,本质都是在寻找一个能最好地描述和解释你手上实际数据的模型。换句话说,理解了这一点,会对你之后学习其他统计模型,理解统计学习(statistical learning)或机器学习有一些帮助吧。
而本书中主要介绍的统计方法,或者说心理统计中使用的绝大多数统计方法都是基于线性模型,也就是基本都假设变量与变量之间的关系是线性的。相比心理专业或者社科背景的读者都会觉得这个假设并不符合现实。确实,选择线性模型并不意味着我们真的认为现实中的情况是这样的,而正是因为现实中的情况是复杂多样的,变量与变量之间的关系可能非常“曲线”,才是我们选择使用线性模型“粗略”地检验它们的原因之一。比如,也许每增加一岁,你的魔法能力增加的幅度并不一样,也许到了30岁你成为魔法师后神功大成增长就相对停滞了。但使用线性模型,我们至少能知道,或者满足于“30岁前,每增加一岁,魔法才能就会增加一点”这个结论。换句话说,我们在传统心理统计中使用线性模型,很大程度上不是为了对数据进行精确拟合和预测,而是粗略地判断变量和变量之间的大致关系如何。11当然,有时变量之间确实存在某种非线性的关系,无法被线性模型直接检验,我们在后面的章节( sec-nonlinear )也稍微介绍了如何使用线性模型对一些非线性关系进行检验。
而要进行精确的预测,我们可能受困于样本量,可能受困于样本和总体之间的信息丢失,我们可能没有办法准确到对总体进行精确的预测。从这个角度上说,心理学和类似的其他学科,现阶段确实更多的研究工作围绕着通过描述和发现现象验证理论(假设),而非对人的心理和行为进行“预测”。也许,要走到“预测“的这一步,也需要统计科学的进一步发展,能让实证研究者以更低的成本更精确地拟合数据,拟合出真正能符合现实情况的模型吧。
不知道读者有没有疑惑,在我们介绍对于回归模型的拟合程度指标时,把它命名为R2。但是,为什么呢?不仅使用了R这个字母,而且还非得加上一个平方,这么命名有什么深意呢。
想想我们的第一摸,相关系数使用的字母是r,这其中是不是有什么关联呢?我们来验证一下。我们在第一摸中的相关系数是:
cor(df1.1$iden_n,df1.1$magic_score)[1] 0.6108072它的平方是:
cor(df1.1$iden_n,df1.1$magic_score) ^2[1] 0.3730855我们之前计算的R2是:
ssb/sst[1] 0.3730855看来,R2 里的R跟r是相等的。换句话说,模型解释的变异占总变异的比例在数值上等于相关的平方。那么,为什么要区分R和r这两个字母呢?我们可以看看另一个相关的计算:
## 生成基于机人和袋人使用回归方程预测的魔法天赋分数
df1.1$magic_score_pre <- predict(lm1)
## 计算生成的预测值和原始数据之间的相关系数
cor(df1.1$magic_score_pre,df1.1$magic_score)[1] 0.6108072## 第一摸中计算的相关系数
cor(df1.1$iden_n,df1.1$magic_score)[1] 0.6108072在上面的代码中,我们计算了一组使用回归模型预测的结果变量(魔法天赋值) ,并计算了它跟结果变量的原始数据 之间的相关。这个相关系数,跟我们之前计算预测变量与结果变量的相关系数相等。这就是R和r的区别。r表示的是预测变量和结果变量两个变量之间的相关。R表示的是模型预测值和结果变量原始数据之间的相关。
有读者会说,既然两个值相等,为什么要搞出这两种相关,用其中一个不就行了?这是因为,就想我们下一章开始马上就会涉及的,一个回归模型含有的预测变量会多于一个,这时候R和r就不相等了。
那么,为什么要把r或者R平方呢?不知道大家还记不记得这个公式 Equation eq-covR ,我们说,r可以看成协方差的标准分数。那么,把r平方之后我们得到了什么呢?
再考虑到 Equation eq-ssq ,相信读者们不难推导出,上面的公式实际上是SSB与SST也是 SSmodel 和 SStotal 的比值。
在上面使用R2的概念时,我们强调的都是模型解释的变异占总变异的比例。我们也介绍了,R对应的是整个模型,r对应的是变量。那么,R2对应的就是SSmodel/SStotal,r2对应的是SSB/SST,这里的SSB,是指自我性别认同这个变量解释的变异。新的问题来了,r2有什么用呢?
如果大家之前学习过方差分析的效应量的概念的话,应该知道通常我们都是使用 及其衍生指标来计算方差分析的效应量。当然,也有很多心理统计教学会直接把R2作为单因素方差分析的效应量指标之一。13无论如何,我们来看看方差分析效应量的计算:
## 计算方差分析的效应量
rstatix::eta_squared(aov1) iden
0.3730855 ## r^2
ssb/sst[1] 0.3730855是的,计算出来的 就是 r2 。这其实就是 的定义,自变量/预测变量对应的变异解释占总变异的比例。它之所以能成为效应量,就是因为它是一个标准化系数的平方,不会因为样本量和变量本身的数值大小而发生变化,而能作为衡量不同组变量之间关系的指标。在这个意义上,其实相关系数本身也能做到一样的事,所以在进行元分析14时,相关系数是一个主要的效应量来源。
到这里,我们基本结束了我们的摸象之旅。这章的撰写时间大大超出了我的想象。不知道你们摸遍这只大象的时候有没有感受到其中的趣味性呢?对我来说,我花了五六年的时间,才逐渐理解了这只大象为什么是一只大象。我不能保证上述的摸法已经穷尽所有,但我希望各位读者不仅满足于知道这是同一只大象;更能在这一前提下,了解不同的摸法,在这只大象身上摸索时,手与手之间会如何彼此触碰,又如何最后融汇成一只大象。我希望,读者们能在这个过程中感受到学习和推导统计的快乐。这种快乐,想必和在物理学中证明波动力学和矩阵力学等价一样,充满了世界之中一切冥冥之中相通的美感。
在将来的统计旅程中,也许你会遇到新的统计方法,新的研究需要,那时如果你能做到手中无象而心中有象,学习和思考的难度会下降很多。所谓“大音希声,大象无形”,这只大象不是t检验,不是方差分析,不是相关,也不是回归,而是联通你对诸多统计方法理解背后的统计思想和逻辑。那么,你就无需自宫而神功大成了。17
对了,多说一句,方差分析和回归分析这些统计模型,当我们把它们视为一只大象时,我们把它叫做一般线性模型(General Linear Model)。这部分的内容是从本科心理统计课程迈上所谓的“高级心理统计”的主要垫脚石。
当然是开个玩笑,对盲人朋友没有什么恶意。↩︎
费马语。↩︎
这里的相关指的是相关这个统计概念,当然为了避免歧义,我们也可以表述成,“关于相关的相关统计知识”。是不是除了像绕口令之外就没有其他问题了呢。↩︎
因为计算机运算取值的关系,R给出的结果是一个无限接近于0的数值,但相信我,它就是零。↩︎
感兴趣的读者可以自己搜索一下相关的数学证明。虽然我觉得用这个证明去理解自由度给的帮助不大。↩︎
比如计算一个量表的分数时,我们可以使用所有题目的分数和,也可以使用所有题目的平均分。做出的统计分析没有差异。平均数的优势是当有缺失值时,量表分数仍然可用。而有常模的量表更多地使用求和,因为更便于使用者解读分数。↩︎
是的,就像我们在t检验中做的那样,用集中趋势代表对于一个样本平均而言每个个体的魔法天赋水平。↩︎
西江月 证明
即得易见平凡,仿照上例显然。留作习题答案略,读者自证不难。
反之亦然同理,推论自然成立,略去过程QED,由上可知证毕。
作者: @Mario Li↩︎
想不明白的读者可以看看上面的表,本质就是所有原始数据的和,就是平均数*人数。↩︎
为什么叫它我们会在下一部分解释。↩︎
这也是你很少看到心理学研究关注模型拟合情况(大多数情况下,R2)的原因之一。当然,你马上会看到,在不是以模型拟合为语境的情况下,对于↩︎
考虑距离为离均差的话,离均差的平方 ,如果已知所有y的取值,试图找到让这个方程取值最小的x值,即二次函数顶点,↩︎
如果你没有学过效应量的相关概念,也可以移步 sec-ecI ,计划中这个番外章会稍微涉及假设检验、效应量以及对应的功效分析。↩︎
对不同研究进行汇总分析的一类研究,也叫荟萃分析。如果我写的开心顺利,将来也许会作为本书的支线简单介绍元分析。↩︎
这里我们使用的“影响”一词指的是一个变量导致了另一个变量发生变化的“影响”,即affect或have an effect on。本书不就近期国内学术圈热烈讨论的 温忠麟 et al. (2025) 与 葛枭语 (2025) 的争端站队。↩︎
注意,这个推导过程并不严谨,也未必严格等价。↩︎
不要问我自宫隐喻了什么,没有那么多为什么,大象已经是我的脑瓜能想出来的绝妙比喻了,别让我耗费脑细胞想别的隐喻了。你非要问,那自宫就是只背怎么点gui做统计或者复制粘贴代码,而不求甚解的做统计吧。↩︎