2 Fundamentos
2.1 Variables regionalizadas
En geostatística se estudian fenómenos que se extienden en el espacio y presentan cierta organización o estructura espacial.
No se trabaja directamente con el fenómeno físico en sí, sino con su representación matemática: una variable regionalizada (o regionalización). Esta se entiende como una función numérica definida en un espacio geográfico que busca describir y medir adecuadamente dicho fenómeno.
Para comprender la idea, pensemos en un fenómeno que se distribuye en un dominio espacial \(D\).
Si realizamos mediciones en diferentes puntos del dominio, obtenemos solo una parte de la información posible, ya que en teoría podrían hacerse infinitas mediciones.
Sin embargo, por limitaciones de tiempo, costo o esfuerzo, solo se recolecta un conjunto finito de datos.
Definición 2.1 Cuando \(s\) recorre el dominio \(D\), el conjunto \(\{z(s), s \in D\}\) se denomina variable regionalizada o regionalización, siendo \(\{z(s_i), i=1,2,3,...\}\) una colección de valores de esa variable y cada valor individual un valor regionalizado.
Un enfoque determinista puede emplearse para describir o modelar un fenómeno regionalizado, proporcionando una estimación precisa de los valores de la regionalización. Sin embargo, este enfoque exige un conocimiento profundo del origen del fenómeno y de las leyes físicas o matemáticas que gobiernan la evolución de la variable regionalizada.
En la práctica, muchos de los fenómenos regionalizados que se estudian son tan complejos que un modelo determinista solo logra representarlos parcialmente. Por esta razón, el enfoque determinista suele ser insuficiente y se recurre al enfoque probabilístico, el cual permite no solo incorporar el conocimiento existente, sino también manejar la incertidumbre asociada al fenómeno aleatorio regionalizado.
2.2 Funciones aleatorias
Desde una perspectiva probabilística, el valor regionalizado puede interpretarse como el resultado de un mecanismo aleatorio, es decir, una variable aleatoria (va).
Si consideramos los valores regionalizados en todos los puntos de un dominio \(D\), podemos verlos como la manifestación de una función aleatoria espacial (también llamada proceso estocástico o campo aleatorio).
Definición 2.2 Cuando \(s\) recorre el dominio bajo estudio \(D\), se tiene una familia de variables aleatorias \(\{Z(s), s \in D\}\), lo cual constituye un campo aleatorio espacial.
Esta decisión metodológica es central en la geoestadística: la variable regionalizada se interpreta como una realización de un campo aleatorio espacial.
La variable regionalizada suele ser altamente irregular en el ámbito local, lo que dificulta su representación mediante funciones deterministas, pero al mismo tiempo presenta una cierta estructura espacial u organización.
El enfoque probabilístico (o geoestadística probabilística) permite considerar ambos aspectos, el errático y el estructurado, de la siguiente manera (Emery (2000)):
- En cada ubicación \(s\), \(Z(s)\) es una variable aleatoria (por lo que tiene un aspecto erráctico).
- Para un conjunto de puntos \(s_1, s_2, \ldots, s_k\), las variables \(Z(s_1), Z(s_2), \ldots, Z(s_k)\) están ligadas por correlaciones espaciales, responsables de la similitud en los valores (aspecto estructurado).
La geoestadística estudia tanto la irregularidad local como la estructura global de las variables regionalizadas como se aprecia en la siguiente figura:
# Paquetes
library(GeoModels) # tu paquete
library(fields) # para drape.plot
set.seed(199)
# Parámetros del modelo exponencial
corrmodel <- "Exponential" # nombre del modelo en GeoModels
parms <- list(mean = 0, # media
sill = 1, # varianza (sill)
nugget = 0, # nugget
scale = 0.25)
# Malla 2D (101 x 101)
step <- 0.01
x <- seq(0, 1, by = step)
y <- seq(0, 1, by = step)
# Simulación del campo gaussiano en grilla
f <- GeoSim(corrmodel = corrmodel,
param = parms,
grid = TRUE,
coordx = x, coordy = y
)$data
# Gráfico 3D
op <- par(mar = c(0,0,0,0), mgp = c(0.5,0.5,0))
drape.plot(x, y, f, col = tim.colors(), theta = 40, phi = 40)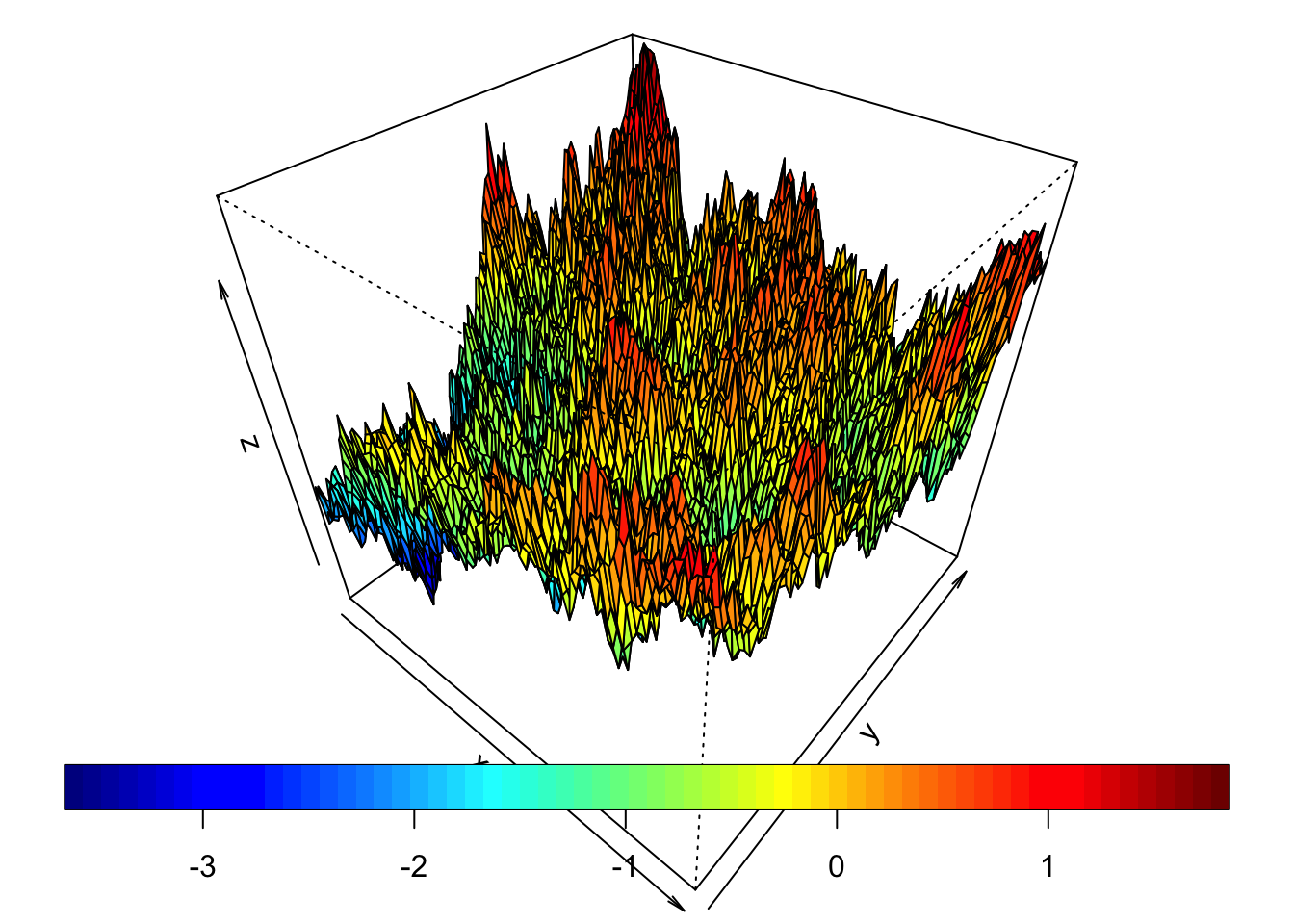
Figura 2.1: Simulación de una variable regionalizada.
Si \(Z(s)\) es un campo aleatorio y consideramos un conjunto de puntos \((s_1, \ldots, s_k)\), entonces \(Z(s)\) se caracteriza por su función de distribución conjunta k-dimensional.
El conjunto de todas estas funciones para distintos \(k\) y combinaciones posibles de puntos en el dominio se denomina ley de probabilidad espacial.
Definición 2.3 Dado un campo aleatorio \(Z(s)\), la función de distribución conjunta k-dimensional se define como:
\[ F(z(s_1), \ldots, z(s_k)) = P[Z(s_1) \leq z(s_1), \ldots, Z(s_k) \leq z(s_k)]. \]
En geoestadística lineal basta con conocer los dos primeros momentos de la distribución de \(Z(s)\).
En la práctica, la información disponible no suele permitir inferir momentos de orden superior.
Los momentos de interés son: media (o primer momento), varianza y covarianza (y de manera equivalente, el semivariograma).
Definición 2.4 (Esperanza o primer momento)
La esperanza de un campo aleatorio se define como una función no aleatoria de \(s\) que coincide en cada punto con el valor esperado de la variable aleatoria en ese lugar:
\[ \mu(s) = E(Z(s)), \quad \forall s \in D. \]
Cuando depende de la ubicación, también se le denomina tendencia (drift) del campo aleatorio.
Definición 2.5 (Varianza)
La varianza de un campo aleatorio se define como una función no aleatoria de \(s\) que coincide en cada punto con la varianza de la variable aleatoria en ese lugar:
\[ V(s) = V(Z(s)), \quad \forall s \in D. \]
Definición 2.6 (Covarianza)
La función de covarianza de un campo aleatorio se define como una función no aleatoria de los puntos \(s_i\) y \(s_j\), tal que para cualquier par de posiciones coincide con la covarianza entre las variables en esos puntos:
\[ C(s_i, s_j) = E\big[(Z(s_i) - \mu(s_i))(Z(s_j) - \mu(s_j))\big], \quad \forall s_i, s_j \in D. \]
Definición 2.7 (Variograma)
El variograma de un campo aleatorio se define como la varianza de las primeras diferencias:
\[ 2\gamma(s_i - s_j) = V\big(Z(s_i) - Z(s_j)\big), \quad \forall s_i, s_j \in D. \]
La función \(\gamma(s_i, s_j)\) recibe el nombre de semivariograma.
Definición 2.8 (Campo gaussiano)
Un campo aleatorio \(Z(s)\) es gaussiano si, para todo \(k\) y cualquier conjunto de puntos \(s_1, \ldots, s_k\), la distribución conjunta de \(Z(s_1), \ldots, Z(s_k)\) es una distribución gaussiana multivariante.
Una distribución gaussiana multivariante se caracteriza por un vector de medias y una matriz de varianzas-covarianzas.
Esto implica que los dos primeros momentos (media y covarianza) determinan completamente su estructura probabilística.
Por esta razón, la suposición de campos gaussianos es común en geoestadística y constituye la base de muchos métodos como el kriging.