잠재성장 모형의 기본 구조
5 잠재성장 모형 (Latent growth model)
5.1 잠재성장 모형 개괄
- 구조방정식 모형을 확장한 분석 방법
- 종단면 자료(longitudinal data)를 분석하는 데 사용
- 동일한 종속변수를 시간 간격을 달리하여 반복 측정한 자료 (즉 패널 자료)에 대한 분석에 적합함
- 시간에 따른 변화를 모델링할 수 있음 \(\to\) 개인 수준의 변화 궤적, 이러한 변화에 영향을 미치는 요인을 분석할 수 있게 해줌
- 전통적인 패널자료 분석기법 (특히 경시적 모형 분석)과의 차이: 잠재변인의 시간에 따른 변화를 모델링함
5.2 주 활용처
- 개인 수준의 변화 측정
- 변화의 속도와 방향 파악
- 변화에 영향을 미치는 요인의 식별
이런 활용이 가능해지면 궁극적으로 인과관계에 대한 더 강력한 추론이 가능해지고, 개인차를 고려한 맞춤형 개입 전략 수립에도 도움이 될 수 있다.
활용례
- 교육 분야에서 학생들의 학업 성취도 변화
- 심리학 분야에서 자아존중감의 변화
- 의학 분야에서 환자의 건강 상태 변화 등
5.3 이론적 배경
5.3.1 기본적인 LGM 모형의 전제들
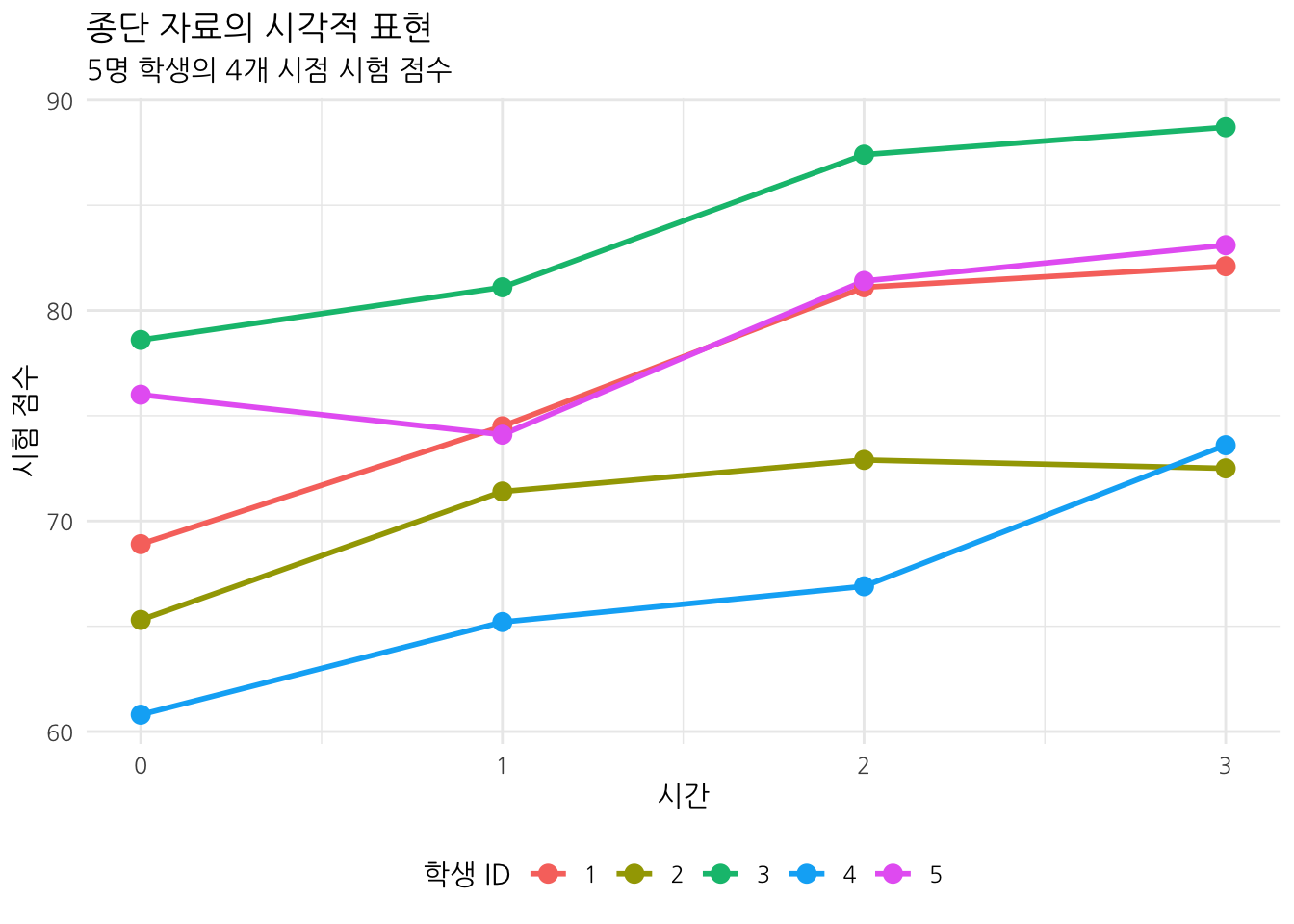
종속변수를 3회 이상 측정: 변화 패턴을 파악하기 위해서는 최소 3회 이상의 측정이 필요. 선형 변화를 파악하려면 최소 3회, 비선형 변화를 파악하려면 4회 이상의 측정이 권장
연속형 변수: 관심 대상 outcome은 등간 또는 비율 척도의 연속형 변수 (예: 시험 점수, 삶의 질, 자아존중감 등).
동일한 시점: 모든 대상에 대해 동일한 시점에 측정되어야 합니다. 예를 들어, 모든 학생이 1학기 중간고사, 1학기 기말고사, 2학기 중간고사, 2학기 기말고사를 치렀어야 함.
동일한 측정 단위: 모든 측정 시점에서 동일한 단위와 척도를 사용해야. 예를 들어, 모든 시험이 100점 만점으로 동일하게 평가되어야 함
| ID | Time | Score |
|---|---|---|
| 1 | 0 | 68.9 |
| 1 | 1 | 74.5 |
| 1 | 2 | 81.1 |
| 1 | 3 | 82.1 |
| 2 | 0 | 65.3 |
| 2 | 1 | 71.4 |
| 2 | 2 | 72.9 |
| 2 | 3 | 72.5 |
| 3 | 0 | 78.6 |
| 3 | 1 | 81.1 |
| 3 | 2 | 87.4 |
| 3 | 3 | 88.7 |
| 4 | 0 | 60.8 |
| 4 | 1 | 65.2 |
| 4 | 2 | 66.9 |
| 4 | 3 | 73.6 |
| 5 | 0 | 76.0 |
| 5 | 1 | 74.1 |
| 5 | 2 | 81.4 |
| 5 | 3 | 83.1 |
5.3.2 모형의 수식 표현
- 1수준 모형
\[Y_{it} = \alpha_i + \beta_i \times \text{Time}_t + \epsilon_{it}\]
- where (2수준 모형):
- \(\alpha_i = \mu_\alpha + \zeta_{\alpha i}\): 개인 \(i\)의 초기값은 평균 초기값(\(\mu_\alpha\))과 개인차(\(\zeta_{\alpha i}\))로 구성.
- \(\beta_i = \mu_\beta + \zeta_{\beta i}\): 개인 \(i\)의 변화율은 평균 변화율(\(\mu_\beta\))과 개인차(\(\zeta_{\beta i}\))로 구성
- 즉, 다시 표현하면
\[Y_{it} = (\mu_\alpha + \zeta_{\alpha i}) + (\mu_\beta + \zeta_{\beta i}) \times \text{Time}_t + \epsilon_{it}\]
- 모수를 정리하면
- 초기값의 평균 (\(\mu_\alpha\))
- 초기값의 분산 (\(\sigma^2_\alpha\))
- 변화율의 평균 (\(\mu_\beta\))
- 변화율의 분산 (\(\sigma^2_\beta\))
- 초기값과 변화율의 공분산 (\(\sigma_{\alpha\beta}\))
- 측정 오차의 분산 (\(\sigma^2_\epsilon\))
5.3.3 선형 및 비선형 모델
잠재성장 모형은 변화 패턴에 따라 다양한 형태로 구성될 수 있다:
- 선형 모델: 시간에 따라 일정한 비율로 변화
- 시간 코딩: 0, 1, 2, 3, …
- 비선형 모델: 시간에 따라 변화율이 달라지는 경우
- 이차 함수 모형: 0, 1, 4, 9, … (시간의 제곱)
- 로그 변환 모형: 0, \(\log(1)\), \(\log(2)\), \(\log(3)\), …
- 자유 추정 모형: 0, \(\lambda_1\), \(\lambda_2\), … (\(\lambda\) 값을 자유롭게 추정)
# 데이터 생성
time_points <- 0:5
linear <- 50 + 5 * time_points
quadratic <- 50 + 2 * time_points^2
log_growth <- 50 + 15 * log(time_points + 1)
free_estimate <- 50 + c(0, 3, 8, 15, 17, 18)
growth_data <- data.frame(
Time = rep(time_points, 4),
Score = c(linear, quadratic, log_growth, free_estimate),
Model = rep(c("선형", "이차함수", "로그함수", "자유추정"), each = length(time_points))
)
# 그래프 그리기
ggplot(growth_data, aes(x = Time, y = Score, color = Model, group = Model)) +
geom_line(size = 1.2) +
geom_point(size = 3) +
theme_minimal(base_family='Nanum Gothic') +
labs(title = "다양한 잠재성장 모형의 성장 곡선",
subtitle = "시간에 따른 측정값 변화 패턴",
x = "시간", y = "측정값") +
theme(legend.position = "bottom",
legend.title = element_text(face = "bold"),
plot.title = element_text(hjust = 0.5, face = "bold"),
plot.subtitle = element_text(hjust = 0.5))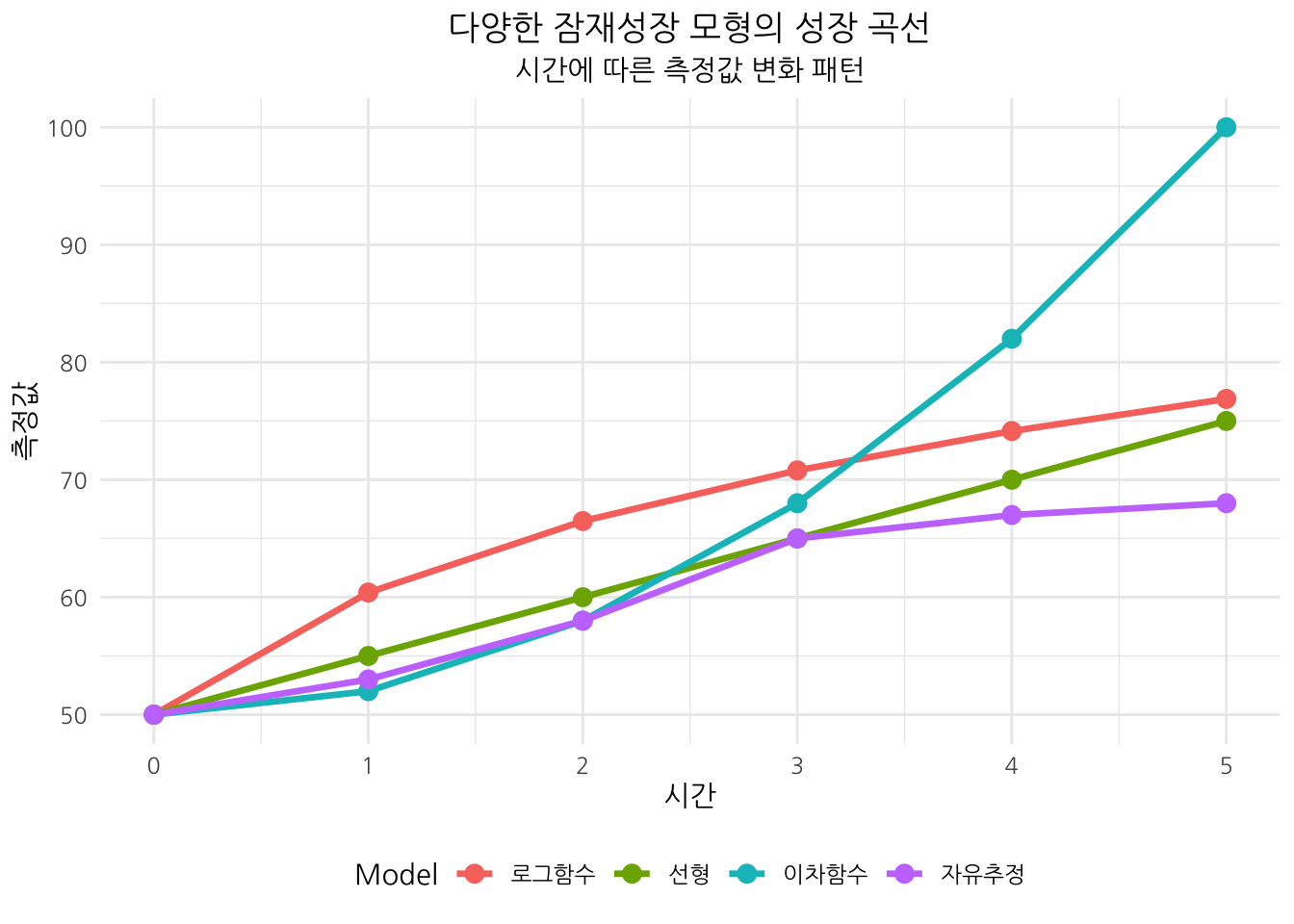
각 모형의 수학적 표현:
- 선형 모델: \(Y_{it} = \alpha_i + \beta_i \times t + \epsilon_{it}\)
- 이차 함수 모델: \(Y_{it} = \alpha_i + \beta_{1i} \times t + \beta_{2i} \times t^2 + \epsilon_{it}\)
- 로그 변환 모델: \(Y_{it} = \alpha_i + \beta_i \times \log(t+1) + \epsilon_{it}\)
- 자유 추정 모델: \(Y_{it} = \alpha_i + \beta_i \times \lambda_t + \epsilon_{it}\) (여기서 \(\lambda_1 = 0\), 나머지 \(\lambda\) 값은 자유롭게 추정)
5.4 R을 활용한 잠재성장 모형 분석
5.4.1 필요 패키지
# 필요 패키지 설치 및 로드
# install.packages(c("lavaan", "semPlot", "tidyverse", "psych"))
library(lavaan) # 구조방정식 및 잠재성장 모형 분석
library(semPlot) # 모형 시각화
library(tidyverse) # 데이터 처리
library(psych) # 기술통계 및 데이터 요약5.4.2 데이터 준비
- 넓은 형식(Wide format): 각 행이 한 개인을 나타내고, 각 시점의 측정값이 별도의 열로 구성
- 패키지를 사용한 잠재성장 모형 분석에 적합
# 넓은 형식 데이터 예시 생성
wide_data <- reshape(long_data, idvar = "ID", timevar = "Time",
direction = "wide")
colnames(wide_data) <- c("ID", "Time0", "Time1", "Time2", "Time3")
# 데이터 확인
head(wide_data) ID Time0 Time1 Time2 Time3
1 1 68.9 74.5 81.1 82.1
5 2 65.3 71.4 72.9 72.5
9 3 78.6 81.1 87.4 88.7
13 4 60.8 65.2 66.9 73.6
17 5 76.0 74.1 81.4 83.1- 긴 형식(Long format): 각 행이 한 개인의 한 시점 측정값을 나타내며, 개인 ID와 시점을 별도의 열로 구성
- 혼합 모형(mixed models) 또는 다층 모형(multilevel models)에 적합
# 긴 형식 데이터 예시 (이미 생성한 long_data 사용)
head(long_data) ID Time Score
1 1 0 68.9
2 1 1 74.5
3 1 2 81.1
4 1 3 82.1
5 2 0 65.3
6 2 1 71.4데이터 형식 변환은 reshape() tidyr::pivot_wider(), tidyr::pivot_longer() 함수 활용
5.4.3 기본 잠재성장 모형 코드
lavaan 패키지를 사용하여 기본적인 선형 잠재성장 모형을 구축하는 방법:
# 선형 잠재성장 모형 정의
lgm_model <- '
# 잠재변수 정의
i =~ 1*Time0 + 1*Time1 + 1*Time2 + 1*Time3 # 초기값(intercept)
s =~ 0*Time0 + 1*Time1 + 2*Time2 + 3*Time3 # 변화율(slope)
# 잠재변수 간 공분산
i ~~ s
# 잠재변수 평균과 분산
i ~ 1 # 초기값의 평균
s ~ 1 # 변화율의 평균
'
# 모형 적합
lgm_fit <- growth(lgm_model, data = wide_data)
# 결과 요약
summary(lgm_fit, fit.measures = TRUE, standardized = TRUE)lavaan 0.6.15 ended normally after 147 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 9
Number of observations 5
Model Test User Model:
Test statistic 9.717
Degrees of freedom 5
P-value (Chi-square) 0.084
Model Test Baseline Model:
Test statistic 37.759
Degrees of freedom 6
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.851
Tucker-Lewis Index (TLI) 0.822
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -50.899
Loglikelihood unrestricted model (H1) -46.040
Akaike (AIC) 119.797
Bayesian (BIC) 116.282
Sample-size adjusted Bayesian (SABIC) 90.708
Root Mean Square Error of Approximation:
RMSEA 0.434
90 Percent confidence interval - lower 0.000
90 Percent confidence interval - upper 0.841
P-value H_0: RMSEA <= 0.050 0.087
P-value H_0: RMSEA >= 0.080 0.906
Standardized Root Mean Square Residual:
SRMR 0.180
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
i =~
Time0 1.000 5.548 0.919
Time1 1.000 5.548 0.910
Time2 1.000 5.548 0.874
Time3 1.000 5.548 0.831
s =~
Time0 0.000 NA NA
Time1 1.000 NA NA
Time2 2.000 NA NA
Time3 3.000 NA NA
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
i ~~
s 1.876 2.388 0.786 0.432 0.509 0.509
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
i 69.966 2.615 26.759 0.000 12.611 12.611
s 3.586 0.371 9.661 0.000 NA NA
.Time0 0.000 0.000 0.000
.Time1 0.000 0.000 0.000
.Time2 0.000 0.000 0.000
.Time3 0.000 0.000 0.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Time0 5.682 4.492 1.265 0.206 5.682 0.156
.Time1 3.080 2.851 1.080 0.280 3.080 0.083
.Time2 3.747 3.272 1.145 0.252 3.747 0.093
.Time3 6.504 5.210 1.248 0.212 6.504 0.146
i 30.781 21.718 1.417 0.156 1.000 1.000
s -0.440 0.775 -0.568 0.570 NA NA위 코드에서: - i =~ 1*Time0 + 1*Time1 + 1*Time2 + 1*Time3: 초기값(intercept) 잠재변수 정의, 모든 시점에 동일한 가중치(1) 부여 - s =~ 0*Time0 + 1*Time1 + 2*Time2 + 3*Time3: 변화율(slope) 잠재변수 정의, 시간에 따른 선형적 가중치 부여 - i ~~ s: 초기값과 변화율 간의 공분산 설정 - i ~ 1, s ~ 1: 초기값과 변화율의 평균 추정
5.4.4 결과 해석
5.4.4.1 모형 적합도 평가
- 카이제곱 검정: χ² = 2.623, df = 5, p = 0.758
- p값이 0.05보다 크므로 모형이 데이터에 적합하다고 볼 수 있음.
- 카이제곱 값이 작고 p값이 크다는 것은 모형과 데이터 간의 차이가 통계적으로 유의미하지 않음을 의미함.
- CFI(Comparative Fit Index): 1.000
- 1에 가까울수록 좋은 적합도를 나타내며, 0.95 이상이면 좋은 적합도로 간주됨.
- 현재 모형의 CFI는 1.000으로 매우 우수함.
- TLI(Tucker-Lewis Index): 1.007
- 1에 가까울수록 좋은 적합도를 나타내며, 0.95 이상이면 좋은 적합도로 간주됨.
- 현재 모형의 TLI는 1.007로 매우 우수함.
- RMSEA(Root Mean Square Error of Approximation): 0.000
- 0.05 이하면 좋은 적합도, 0.08 이하면 수용 가능한 적합도로 간주됨.
- 현재 모형의 RMSEA는 0.000으로 매우 우수함.
- 90% 신뢰구간은 [0.000, 0.096]으로, 상한값이 0.1 미만이므로 적합도가 양호함.
- SRMR(Standardized Root Mean Square Residual): 0.030
- 0.08 이하면 좋은 적합도로 간주됨.
- 현재 모형의 SRMR은 0.030으로 우수함.
5.4.4.2 모형 적합도 평가
잠재변수 계수(요인 적재량): - 초기값(i)에 대한 요인 적재량은 모든 시점에서 1.000으로 고정됨. - 변화율(s)에 대한 요인 적재량은 시간에 따라 0, 1, 2, 3으로 설정되어 선형 성장을 가정함.
공분산: - 초기값(i)과 변화율(s)의 공분산: 0.633 (p = 0.613) - p값이 0.05보다 크므로 통계적으로 유의미하지 않음. - 이는 초기값과 변화율 사이에 유의미한 관계가 없음을 의미함. - 표준화된 공분산은 0.097로, 초기값과 변화율 사이에 약한 양의 상관관계가 있지만 통계적으로 유의미하지 않음.
평균: - 초기값(i)의 평균: 61.408 (p < 0.001) - 통계적으로 매우 유의미함. - 이는 첫 번째 시점에서의 평균 점수가 약 61.4점임을 의미함.
- 변화율(s)의 평균: 5.065 (p < 0.001)
- 통계적으로 매우 유의미함.
- 이는 시간이 한 단위 증가할 때마다 점수가 평균적으로 약 5.1점씩 증가함을 의미함.
분산: - 초기값(i)의 분산: 41.416 (p < 0.001) - 통계적으로 매우 유의미함. - 이는 첫 번째 시점에서 학생들 간의 점수 차이가 상당히 크다는 것을 의미함.
- 변화율(s)의 분산: 1.029 (p = 0.046)
- 통계적으로 유의미함.
- 이는 시간에 따른 점수 변화율에 있어 학생들 간에 유의미한 차이가 있음을 의미함.
5.4.4.3 해석 요약
기본 잠재성장 모형 분석 결과, 모형은 데이터에 매우 적합한 것으로 나타남. 학생들의 초기 평균 점수는 약 61.4점이며, 시간이 지남에 따라 평균적으로 매 시점마다 약 5.1점씩 증가하는 것으로 나타남. 초기값과 변화율 모두 학생들 간에 유의미한 차이가 있었으나, 초기값과 변화율 사이의 관계는 통계적으로 유의미하지 않았음. 이는 초기 점수가 높거나 낮은 학생들이 반드시 더 빠르거나 느리게 성장하는 것은 아님을 시사함.
5.4.5 모형 시각화
# 모형 시각화
semPaths(lgm_fit, what = "est", layout = "tree2",
edge.label.cex = 0.8, curvePivot = TRUE,
title = FALSE, residuals = TRUE,
sizeMan = 8, sizeLat = 10,
edge.color = "black", node.color = c("lightblue", "lightgreen"))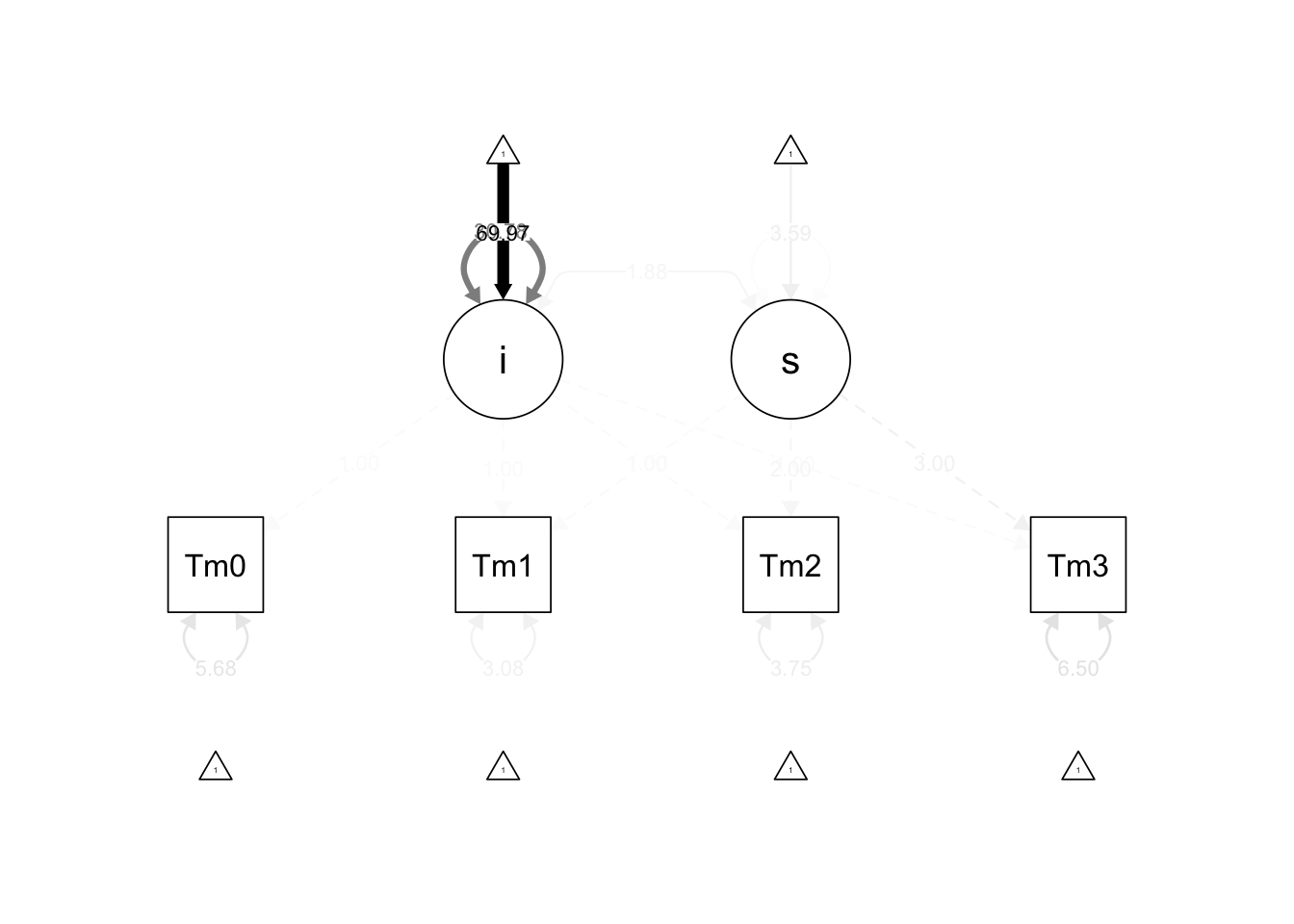
5.4.6 개인별 성장 궤적 시각화
# 개인별 성장 궤적 시각화
ggplot(long_data, aes(x = Time, y = Score, group = ID, color = factor(ID))) +
geom_line(size = 1.2) +
geom_point(size = 3) +
theme_minimal(base_family='Nanum Gothic') +
labs(title = "개인별 성장 궤적",
subtitle = "시간에 따른 개인별 측정값 변화",
x = "시간", y = "측정값",
color = "ID") +
theme(legend.position = "bottom",
plot.title = element_text(hjust = 0.5, face = "bold"),
plot.subtitle = element_text(hjust = 0.5))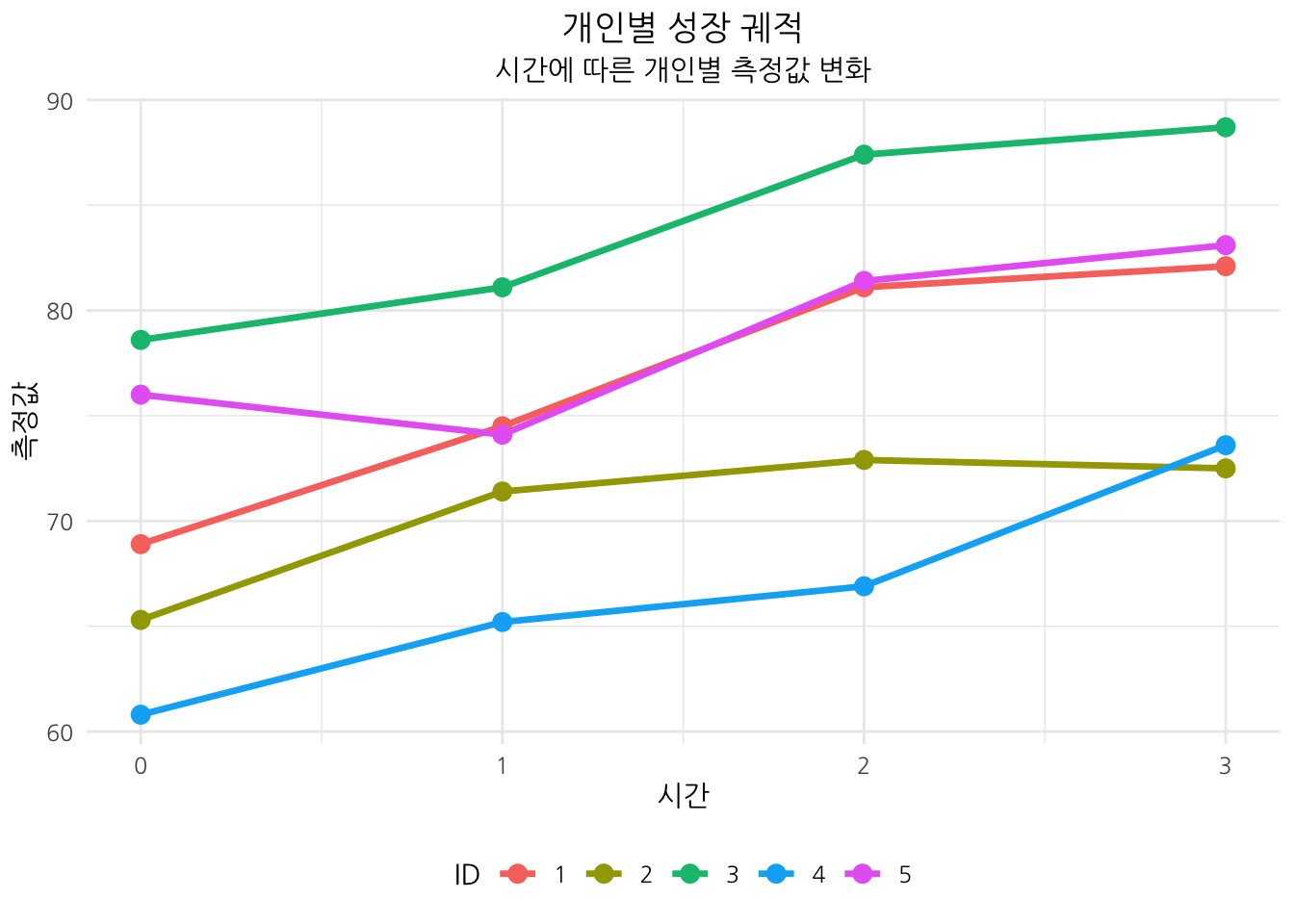
5.5 실제 데이터를 활용한 잠재성장모형 예제
5.5.1 (1) 신경 위험 처리의 변화에 대한 잠재성장모형 분석
이 예제는 Rex B. Kline의 “Principles and Practice of Structural Equation Modeling” 5판의 21장에서 제시된 실제 데이터를 활용한 분석임. 이 연구는 청소년의 신경 위험 처리(neural risk processing)가 14-17세 사이에 어떻게 변화하는지 분석한 것임.
5.5.1.1 데이터 소개
이 연구에서는 150명의 청소년을 대상으로 14세부터 17세까지 4년간 신경 위험 처리(R1, R2, R3, R4)를 측정함. 또한 학대(abuse)와 방치(neglect) 경험에 대한 정보도 수집됨. 데이터는 상관행렬과 평균, 표준편차 형태로 제공됨.
# 상관행렬 입력
kimspoonLower.cor <- '
1.00
.35 1.00
.28 .35 1.00
.29 .40 .45 1.00
.00 .07 .14 .04 1.00
.00 -.09 -.12 -.10 .26 1.00 '
# 변수명 지정 및 전체 상관행렬로 변환
kimspoon.cor <- lavaan::getCov(kimspoonLower.cor, names = c("R1", "R2",
"R3", "R4", "abuse", "neglect"))
# 상관행렬 출력
kimspoon.cor
# 표준편차를 추가하여 공분산 행렬로 변환
kimspoon.cov <- lavaan::cor2cov(kimspoon.cor, sds = c(.05,.77,.76,1.15,
7.75,4.09))
# 평균 벡터 생성
kimspoon.mean = c(.04,.61,.57,.83,7.17,3.03)
# 공분산 행렬과 평균 출력
kimspoon.cov
kimspoon.mean5.5.1.2 모형 비교
이 연구에서는 세 가지 모형을 비교함:
- 무성장 모형(No Growth Model): 시간에 따른 변화가 없다고 가정
- 잠재기반 성장모형(Latent Basis Growth Model): 비선형 변화를 자유롭게 추정
- 선형 성장모형(Linear Growth Model): 시간에 따라 일정한 비율로 변화
# 모형 1: 무성장 모형
noGrowth.model <- '
# 초기값만 포함
Intercept =~ 1*R1 + 1*R2 + 1*R3 + 1*R4
# R1의 오차분산을 0으로 고정
R1 ~~ 0*R1 '
# 모형 2: 잠재기반 성장모형
basis.model <- '
Intercept =~ 1*R1 + 1*R2 + 1*R3 + 1*R4
# 형태 요인, 첫 번째와 마지막 요인 적재량 고정
Shape =~ 0*R1 + R2 + R3 + 1*R4
R1 ~~ 0*R1 '
# 모형 3: 선형 성장모형
linear.model <- '
Intercept =~ 1*R1 + 1*R2 + 1*R3 + 1*R4
# 모든 요인 적재량을 상수로 고정
Linear =~ 0*R1 + 1*R2 + 2*R3 + 3*R4
R1 ~~ 0*R1 '
# 모형 적합
noGrowth <- lavaan::growth(noGrowth.model, sample.cov = kimspoon.cov,
sample.mean = kimspoon.mean, sample.nobs = 150)
basis <- lavaan::growth(basis.model, sample.cov = kimspoon.cov,
sample.mean = kimspoon.mean, sample.nobs = 150)
linear <- lavaan::growth(linear.model, sample.cov = kimspoon.cov,
sample.mean = kimspoon.mean, sample.nobs = 150)5.5.1.3 모형 비교 결과
# 모형 카이제곱 및 카이제곱 차이 검정
anova(noGrowth, basis)
anova(basis, linear)모형 비교 결과, 무성장 모형은 매우 적합도가 낮았으며(χ² = 267.63, df = 9, p < 0.001), 잠재기반 성장모형이 선형 성장모형보다 데이터에 더 적합한 것으로 나타남(Δχ² = 32.00, df = 2, p < 0.001). 따라서 잠재기반 성장모형을 최종 모형으로 선택함.
5.5.1.4 최종 모형 분석 결과
# 최종 모형(잠재기반 성장모형) 결과 요약
summary(basis, fit.measures = TRUE, rsquare = TRUE)최종 모형의 적합도는 매우 우수했음(χ² = 2.81, df = 4, p = 0.59, CFI = 1.00, RMSEA = 0.00). 주요 결과는 다음과 같음:
- 초기값(Intercept)의 평균은 0.040(p < 0.001)으로, 14세 시점의 평균 신경 위험 처리 수준을 나타냄.
- 형태(Shape) 요인의 평균은 0.817(p < 0.001)로, 시간에 따라 신경 위험 처리가 증가함을 보여줌.
- R2와 R3의 요인 적재량은 각각 0.678과 0.646으로 추정되었으며, 이는 비선형적인 변화 패턴을 나타냄.
- 초기값과 형태 요인 간의 공분산은 0.014(p < 0.001)로, 초기 신경 위험 처리 수준이 높을수록 시간에 따른 증가율도 높은 경향이 있음을 보여줌.
- R-제곱 값은 R1에서 1.000, R2에서 0.407, R3에서 0.388, R4에서 0.408로, 모형이 종속변수 분산의 상당 부분을 설명함을 보여줌.
5.5.1.5 결론
이 연구 결과는 청소년의 신경 위험 처리가 14-17세 사이에 비선형적으로 증가함을 보여줌. 특히, 초기 수준이 높은 청소년일수록 시간에 따른 증가율도 높은 경향이 있었음. 이러한 결과는 청소년기 신경 발달에 대한 중요한 통찰을 제공하며, 위험 처리 능력의 발달 궤적이 단순한 선형 패턴을 따르지 않음을 시사함.
5.5.2 (2) 청소년 알코올 사용 변화 예측 모형
이 예제는 Rex B. Kline의 “Principles and Practice of Structural Equation Modeling” 5판의 21장에서 제시된 두 번째 실제 데이터 분석임. 이 연구는 13-16세 청소년의 알코올 사용 변화를 예측하는 모형을 분석함.
5.5.2.1 데이터 소개
이 연구에서는 321명의 청소년을 대상으로 13세부터 16세까지 4년간 알코올 사용(a1, a2, a3, a4)을 측정함. 예측변수로는 성별(gender)과 가족 관계(family)가 포함됨. 데이터는 상관행렬과 평균, 표준편차 형태로 제공됨.
# 상관행렬 입력
duncanLower.cor <- '
1.000
.640 1.000
.586 .670 1.000
.454 .566 .621 1.000
.001 .038 .118 .091 1.000
.214 .149 .135 .163 .025 1.000 '
# 변수명 지정 및 전체 상관행렬로 변환
duncan.cor <- lavaan::getCov(duncanLower.cor, names = c("a1", "a2",
"a3", "a4", "gender", "family"))
# 상관행렬 출력
duncan.cor
# 표준편차를 추가하여 공분산 행렬로 변환
duncan.cov <- lavaan::cor2cov(duncan.cor, sds = c(1.002,.960,.912,.920,
.504,.498))
# 평균 벡터 생성
duncan.mean = c(2.271,2.560,2.694,2.965,.573,.446)
# 공분산 행렬과 평균 출력
duncan.cov
duncan.mean5.5.2.2 조건부 성장모형
이 연구에서는 성별과 가족 관계를 예측변수로 하는 조건부 선형 성장모형을 분석함.
# 조건부 성장모형 정의
predict.model <- '
# 잠재 성장 요인
Intercept =~ 1*a1 + 1*a2 + 1*a3 + 1*a4
Linear =~ 0*a1 + 1*a2 + 2*a3 + 3*a4
# 공변량
Intercept ~ gender + family
Linear ~ gender + family '
# 예측 모형 적합
predict <- lavaan::growth(predict.model, sample.cov = duncan.cov,
sample.mean = duncan.mean, sample.nobs = 321)5.5.2.3 분석 결과
# 모형 결과 요약
summary(predict, fit.measures = TRUE, rsquare = TRUE)모형의 적합도는 양호했음(χ² = 13.82, df = 9, p = 0.129, CFI = 0.992, RMSEA = 0.041). 주요 결과는 다음과 같음:
- 초기값 예측:
- 성별은 초기 알코올 사용 수준에 유의미한 영향을 미치지 않았음(β = 0.011, p = 0.918).
- 가족 관계는 초기 알코올 사용 수준에 유의미한 영향을 미쳤음(β = 0.377, p < 0.001). 가족 관계 점수가 높을수록 초기 알코올 사용 수준이 높았음.
- 변화율 예측:
- 성별은 알코올 사용 변화율에 경계선상의 유의미한 영향을 미쳤음(β = 0.065, p = 0.065). 여학생이 남학생보다 알코올 사용 증가율이 약간 높은 경향이 있었음.
- 가족 관계는 알코올 사용 변화율에 유의미한 영향을 미치지 않았음(β = -0.044, p = 0.216).
- 잠재변수 간 관계:
- 초기값과 변화율 간의 공분산은 -0.077(p < 0.001)로, 초기 알코올 사용 수준이 높을수록 시간에 따른 증가율이 낮은 경향이 있었음. 이는 천장 효과(ceiling effect)를 시사할 수 있음.
- 설명력:
- 모형은 초기값 분산의 5.0%와 변화율 분산의 3.9%를 설명함.
- 관측변수(a1-a4)의 R-제곱 값은 0.643-0.678로, 모형이 알코올 사용 측정치의 상당 부분을 설명함을 보여줌.
5.5.2.4 결론
이 연구 결과는 청소년의 알코올 사용이 13-16세 사이에 선형적으로 증가함을 보여줌. 가족 관계는 초기 알코올 사용 수준에 유의미한 영향을 미쳤으나, 시간에 따른 변화율에는 유의미한 영향을 미치지 않았음. 성별은 변화율에 경계선상의 영향을 미쳤으며, 여학생이 남학생보다 알코올 사용 증가율이 약간 높은 경향이 있었음. 또한, 초기 알코올 사용 수준이 높은 청소년일수록 시간에 따른 증가율이 낮은 경향이 있었음.
| 저자 | 제목 | 출판정보 |
|---|---|---|
| Bollen, K. A., & Curran, P. J. | Latent curve models: A structural equation perspective | Wiley (2006) |
| Duncan, T. E., & Duncan, S. C. | An introduction to latent growth curve modeling | Behavior Therapy, 35(2), 333-363 (2004) |
| Preacher, K. J., Wichman, A. L., MacCallum, R. C., & Briggs, N. E. | Latent growth curve modeling | Sage (2008) |
| Grimm, K. J., Ram, N., & Estabrook, R. | Growth modeling: Structural equation and multilevel modeling approaches | Guilford Publications (2016) |
| Little, T. D. | Longitudinal structural equation modeling | Guilford Press (2013) |
| Muthén, B., & Muthén, L. | Mplus user’s guide | Muthén & Muthén (2017) |
| Singer, J. D., & Willett, J. B. | Applied longitudinal data analysis: Modeling change and event occurrence | Oxford University Press (2003) |
5.6 부록: 핵심 R 코드 모음
# 필요 패키지 설치 및 로드
install.packages(c("lavaan", "semPlot", "tidyverse", "psych"))
library(lavaan)
library(semPlot)
library(tidyverse)
library(psych)
# 데이터 형식 변환
# 긴 형식 -> 넓은 형식
wide_data <- reshape(long_data, idvar = "ID", timevar = "Time", direction = "wide")
# 넓은 형식 -> 긴 형식
long_data <- reshape(wide_data, idvar = "ID",
varying = c("Time0", "Time1", "Time2", "Time3"),
v.names = "Score", timevar = "Time", direction = "long")
# 기본 선형 잠재성장 모형
lgm_model <- '
# 잠재변수 정의
i =~ 1*Time0 + 1*Time1 + 1*Time2 + 1*Time3
s =~ 0*Time0 + 1*Time1 + 2*Time2 + 3*Time3
# 잠재변수 간 공분산
i ~~ s
# 잠재변수 평균과 분산
i ~ 1
s ~ 1
'
# 모형 적합
lgm_fit <- growth(lgm_model, data = wide_data)
# 결과 요약
summary(lgm_fit, fit.measures = TRUE, standardized = TRUE)
# 모형 시각화
semPaths(lgm_fit, what = "est", layout = "tree2")
# 이차 함수 모형
quadratic_model <- '
# 잠재변수 정의
i =~ 1*Time0 + 1*Time1 + 1*Time2 + 1*Time3
s =~ 0*Time0 + 1*Time1 + 2*Time2 + 3*Time3
q =~ 0*Time0 + 1*Time1 + 4*Time2 + 9*Time3
# 잠재변수 간 공분산
i ~~ s
i ~~ q
s ~~ q
# 잠재변수 평균과 분산
i ~ 1
s ~ 1
q ~ 1
'
# 조건부 모형 (예측변수 포함)
conditional_model <- '
# 잠재변수 정의
i =~ 1*Time0 + 1*Time1 + 1*Time2 + 1*Time3
s =~ 0*Time0 + 1*Time1 + 2*Time2 + 3*Time3
# 예측변수의 영향
i ~ predictor
s ~ predictor
# 잠재변수 간 공분산
i ~~ s
'
# 다중 그룹 분석
mgrowth(lgm_model, data = wide_data, group = "group_variable")