22 Day 22 (April 10)

22.1 Announcements

  • April check-in is worth 5% of your grade. Please send email to both Aidan and I to plan your April check in.

  • Selected questions/clarifications from journals

    • Most questions are now project related.
    • “I am currently struggling with the idea of what makes data”good” or “bad” and how that affects the design of a study.”
    • “f you say you measured someone’s height, but the measurement method was poor or inconsistent, then the data may not be trustworthy at all….”

22.2 Gaussian process

  • A Gaussian process is a probability distribution over functions
    • If the function is observed at a finite number of points or “locations,” then the vector of values follows a multivariate normal distribution.

22.2.1 Multivariate normal distribution

  • Multivariate normal distribution

    • \(\boldsymbol{\eta}\sim\text{N}(\mathbf{0},\sigma^{2}\mathbf{R})\)
    • Definitions
      • Correlation matrix – A positive semi-definite matrix whose elements are the correlation between observations
      • Correlation function – A function that describes the correlation between observations
    • Example correlation matrices
      • Compound symmetry \[\mathbf{R}=\left[\begin{array}{cccccc} 1 & 1 & 0 & 0 & 0 & 0\\ 1 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 1 & 0 & 0\\ 0 & 0 & 1 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 1\\ 0 & 0 & 0 & 0 & 1 & 1 \end{array}\right]\]
      • AR(1) \[\mathbf{R(\phi})=\left[\begin{array}{ccccc} 1 & \phi^{1} & \phi^{2} & \cdots & \phi^{n-1}\\ \phi^{1} & 1 & \phi^{1} & \cdots & \phi^{n-2}\\ \phi^{2} & \phi^{1} & 1 & \vdots & \phi^{n-3}\\ \vdots & \vdots & \vdots & \ddots & \ddots\\ \phi^{n-1} & \phi^{n-2} & \phi^{n-3} & \ddots & 1 \end{array}\right]\:\]

  • Example simulating from \(\boldsymbol{\eta}\sim\text{N}(\mathbf{0},\sigma^{2}\mathbf{R})\) in R

    n <- 200
x <- 1:n
I <- diag(1, n)
sigma2 <- 1

library(MASS)
set.seed(2034)
eta <- mvrnorm(1, rep(0, n), sigma2 * I)
cor(eta[1:(n - 1)], eta[2:n])
    ## [1] -0.06408623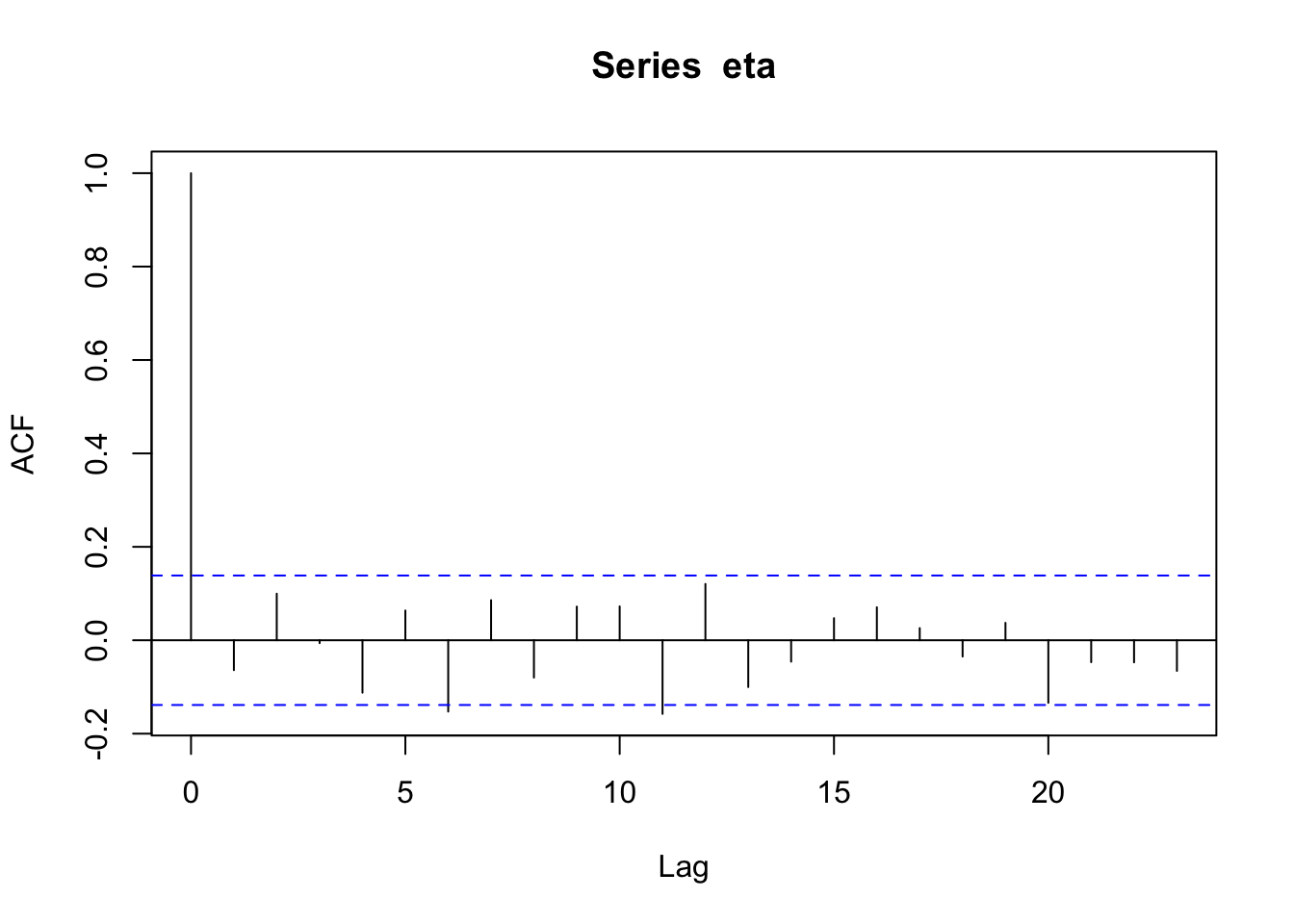
    acf(eta)

    par(mfrow = c(2, 1))
par(mar = c(0, 2, 0, 0), oma = c(5.1, 3.1, 2.1, 2.1))
plot(x, eta, typ = "l", xlab = "", xaxt = "n")
abline(a = 0, b = 0)

n <- 200
x <- 1:n # Must be equally spaced
phi <- 0.7
R <- phi^abs(outer(x, x, "-"))
sigma2 <- 1
set.seed(1330)
eta <- mvrnorm(1, rep(0, n), sigma2 * R)
cor(eta[1:(n - 1)], eta[2:n])
    ## [1] 0.7016481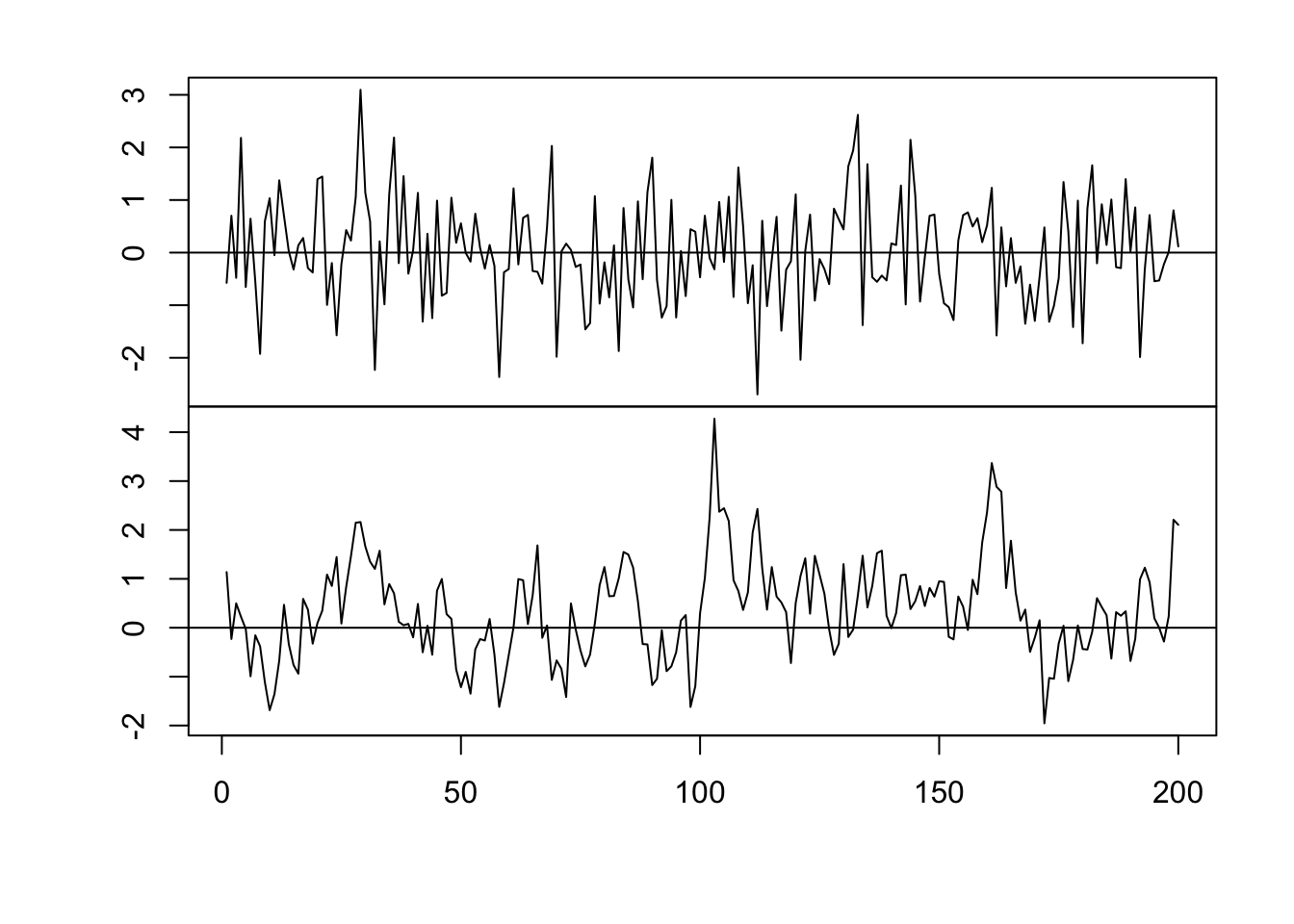
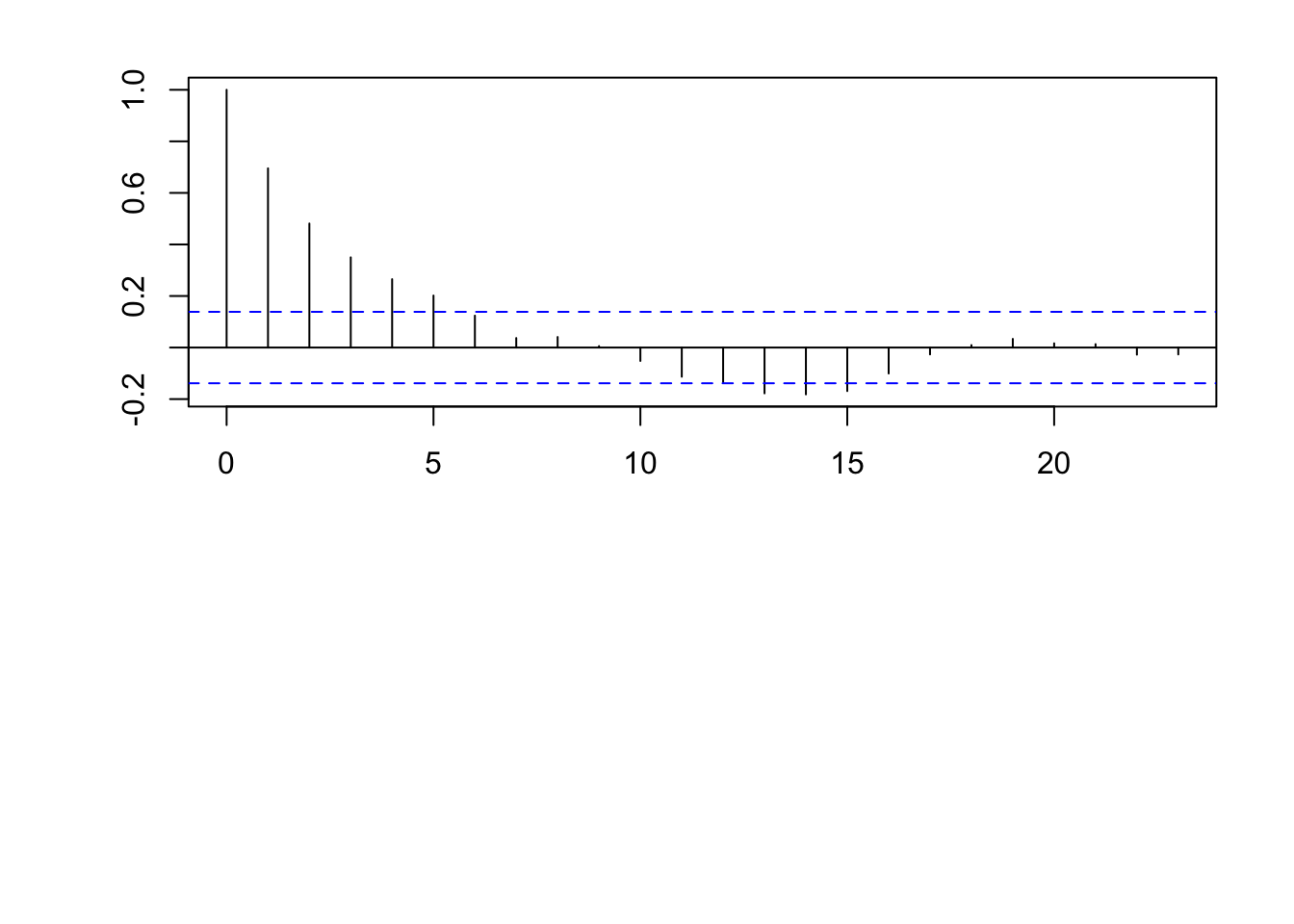
    plot(x, eta, typ = "l")
abline(a = 0, b = 0)

    acf(eta)

    • Example correlation functions
      • Gaussian correlation function \[r_{ij}(\phi)=e^{-\frac{d_{ij}^{2}}{\phi}}\] where \(d_{ij}\) is the “distance” between locations i and j (note that \(d_{ij}=0\) for \(i=j\)) and \(r_{ij}(\phi)\) is the element in the \(i^{\textrm{th}}\) row and \(j^{\textrm{th}}\) column of \(\mathbf{R}(\phi)\).
    library(fields)
n <- 200
x <- 1:n
phi <- 40
d <- rdist(x)
R <- exp(-d^2/phi)
sigma2 <- 1

set.seed(4673)
eta <- mvrnorm(1, rep(0, n), sigma2 * R)
plot(x, eta, typ = "l")
abline(a = 0, b = 0)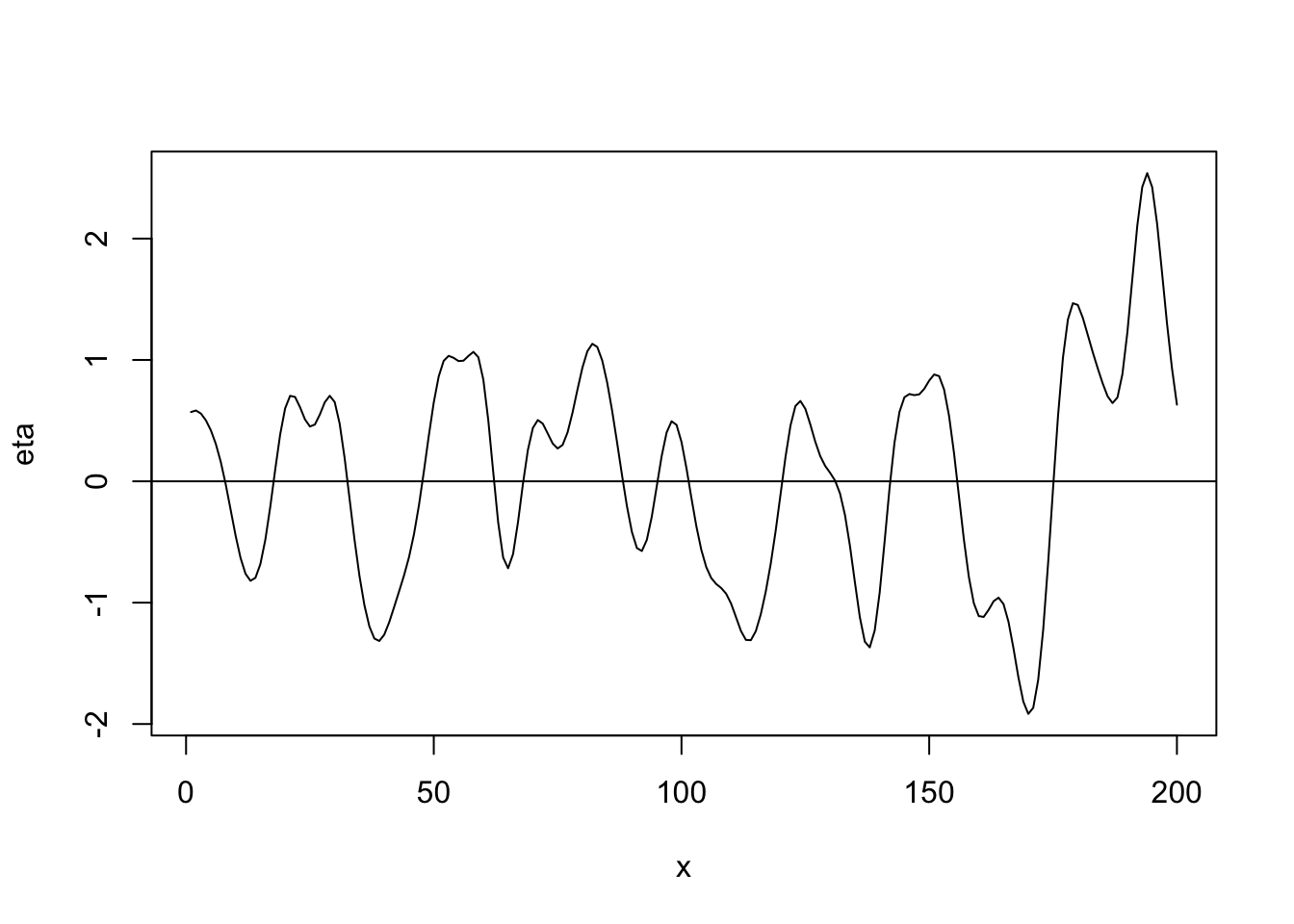

    cor(eta[1:(n-1)], eta[2:n])
    ## [1] 0.9717508
    • Linear correlation function \[r_{ij}(\phi)=\begin{cases} 1-\frac{d_{ij}}{\phi} &\text{if}\ d_{ij}<0\\ 0 &\text{if}\ d_{ij}>0 \end{cases}\]
    library(fields)
n <- 200
x <- 1:n
phi <- 40
d <- rdist(x)
R <- ifelse(d<phi,1-d/phi,0)
sigma2 <- 1

set.seed(4803)
eta <- mvrnorm(1, rep(0, n), sigma2 * R)
plot(x, eta, typ = "l")
abline(a = 0, b = 0)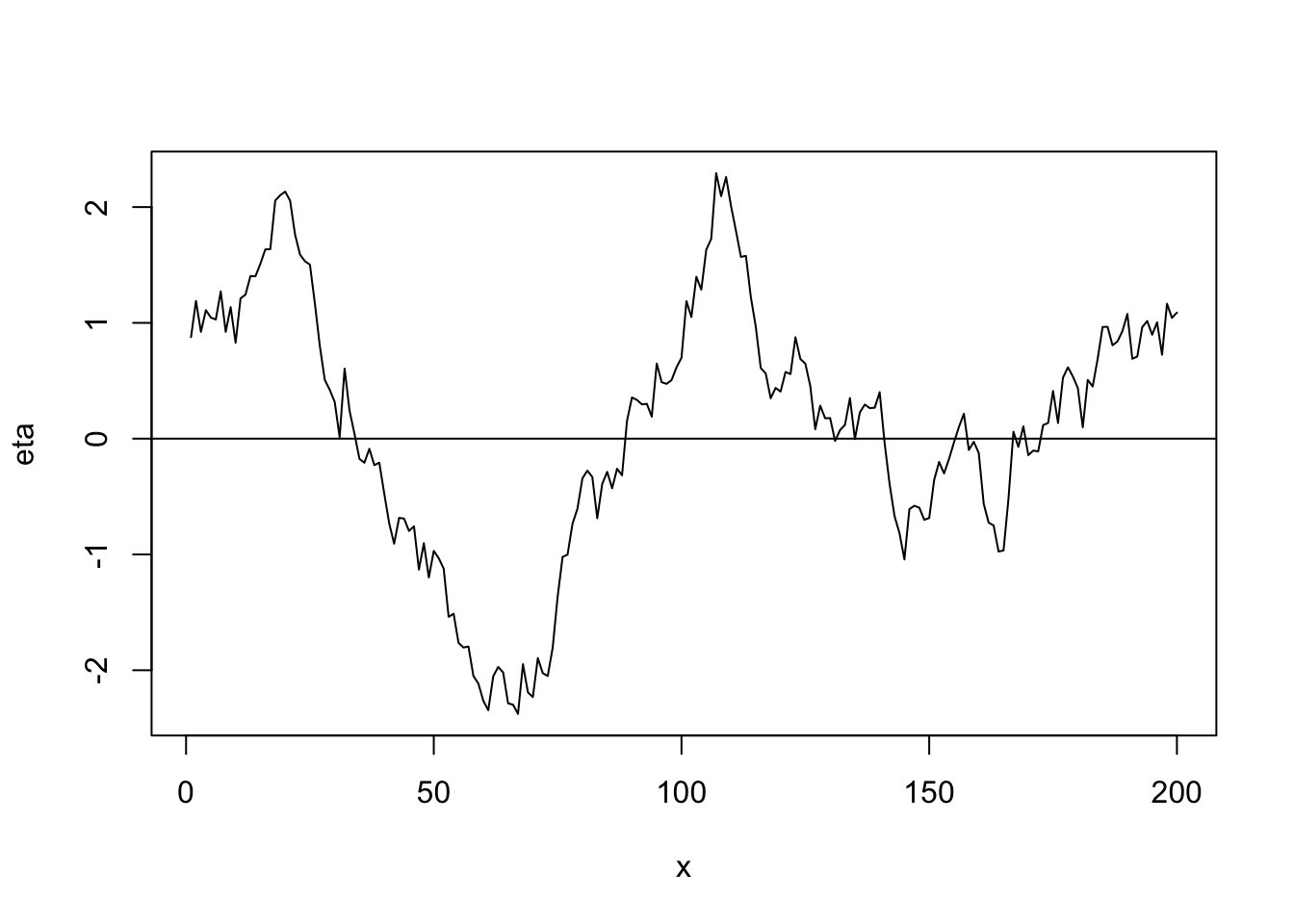

    cor(eta[1:(n-1)], eta[2:n])
    ## [1] 0.9778878

    Bayesian Kriging

  • Read Chapter 17

  • Example data set

    url <- "https://www.dropbox.com/s/k2ajjvyxwvsbqgf/ISIT.txt?dl=1"
df <- read.table(url, header = TRUE)
df <- df[df$Station == 16,c(1,2,5,6)]

head(df)
    ##     Depth Sources Latitude Longitude
## 595   598   53.37  49.0322  -16.1493
## 596   631   51.32  49.0322  -16.1493
## 597   700   42.42  49.0322  -16.1493
## 598   666   38.32  49.0322  -16.1493
## 599  1317   37.29  49.0322  -16.1493
## 600  1352   36.27  49.0322  -16.1493
    plot(df$Depth, df$Sources, las = 1, ylim = c(0, 65), col = rgb(0, 0, 0, 0.25),
 pch = 19, xlab = "Depth (m)", ylab = "Sources")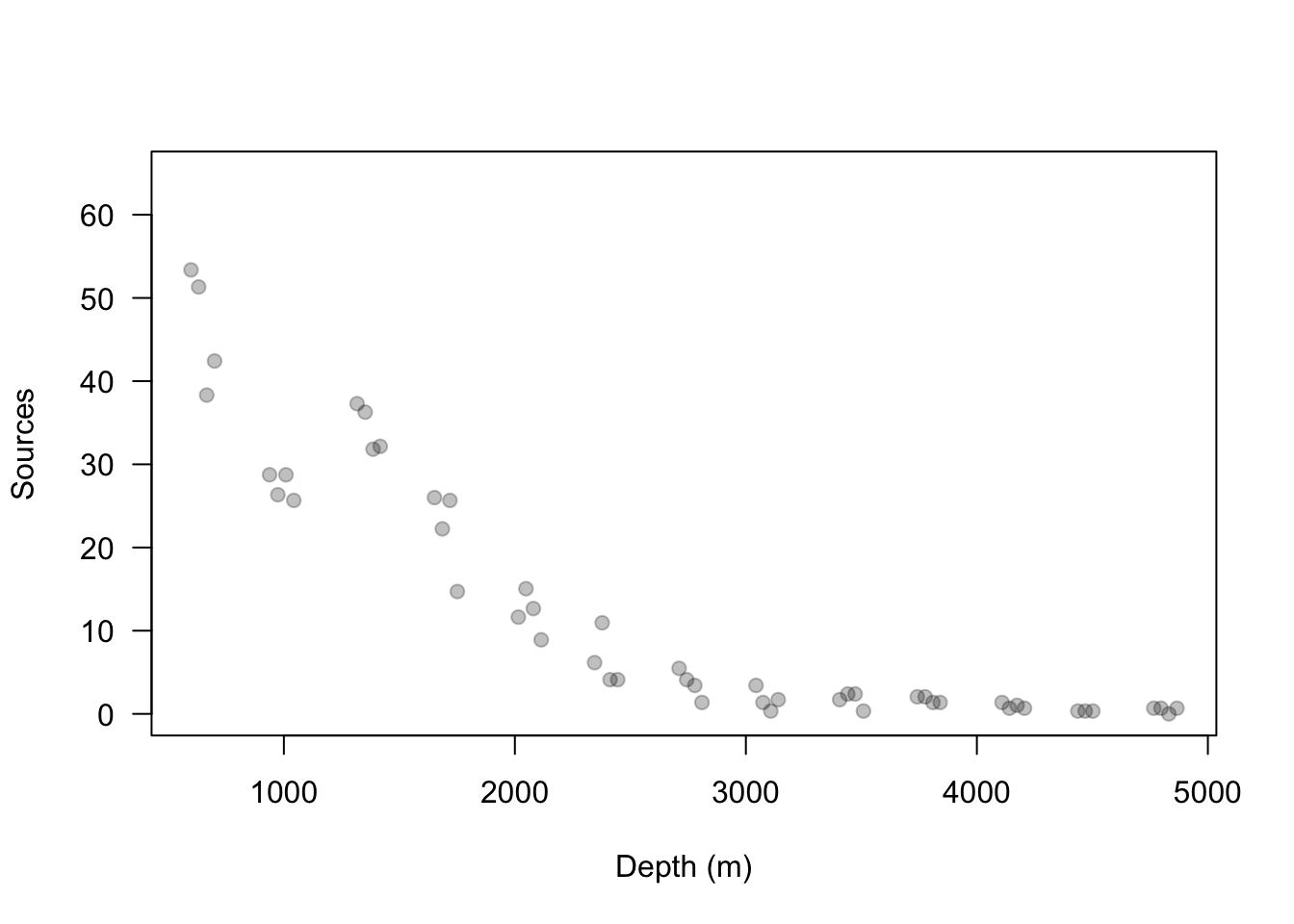

  • Modify the linear model

    • Account for spatial autocorrelation
    • Enable prediction at locations
    • Write out on whiteboard
    • In R
    library(fields)
library(truncnorm)
library(mvtnorm)
library(coda)
library(MASS)

y <- df$Sources
X <- model.matrix(~I(Depth/Depth)-1,data=df)
Z <- diag(1,length(y))
n <- length(y)

# Distance matrix used to calculate correlation matrix
D <- rdist(df$Depth)

m.draws <- 10000  #Number of MCMC samples to draw
samples <- as.data.frame(matrix(,m.draws+1,dim(X)[2]+3))
colnames(samples) <- c(colnames(X),"sigma2.e","sigma2.alpha","phi")
samples[1,] <- c(40,10,150,250)  #Starting values for beta0, sigma2.e, sigma2.alpha, and phi
samples.alpha <- as.data.frame(matrix(,m.draws+1,length(y)))

# Hyperparameters for priors
sigma2.beta <- 100 
a <- 2.01 
b <- 1
c <- 2.01 
d <- 1
e <- 0
f <- 10^6

accept <- matrix(, m.draws + 1, 1) # Monitor acceptance rate
colnames(accept) <- c("phi")
phi.tune <- 10

set.seed(3909)
ptm <- proc.time()
for(k in 1:m.draws){
  beta <- t(samples[k,1:dim(X)[2]])
  sigma2.e <- samples[k,dim(X)[2]+1]
  sigma2.alpha <- samples[k,dim(X)[2]+2]
  phi <- samples[k,dim(X)[2]+3]
  C <- exp(-(D/phi)^2)
  CI <- solve(C)

  # Sample alpha
  H <- solve((1/sigma2.e)*t(Z)%*%Z + (1/sigma2.alpha)*CI)
  h <- (1/sigma2.e)*t(Z)%*%(y-X%*%beta)
  alpha <-  mvrnorm(1,H%*%h,H)

  # Sample beta
  H <- solve((1/sigma2.e)*t(X)%*%X + (1/sigma2.beta)*diag(1,dim(X)[2]))
  h <- (1/sigma2.e)*t(X)%*%(y-Z%*%alpha)
  beta <-  mvrnorm(1,H%*%h,H)

  # Sample sigma2.alpha
  sigma2.alpha <- 1/rgamma(1,a+n/2,b+t(alpha)%*%CI%*%(alpha)/2)

  # Sample sigma2.e
  sigma2.e <- 1/rgamma(1,c+n/2,d+t(y-X%*%beta-Z%*%alpha)%*%(y-X%*%beta-Z%*%alpha)/2)

  #Sample phi
  phi.star <- rnorm(1,phi,phi.tune)
  if(phi.star > e & phi.star < f){
C.star <-  exp(-(D/phi.star)^2)
mh1 <- dmvnorm(alpha,rep(0,n),sigma2.alpha*C.star,log=TRUE) + dunif(phi.star,e,f,log=TRUE)
mh2 <- dmvnorm(alpha,rep(0,n),sigma2.alpha*C,log=TRUE) + dunif(phi,e,f,log=TRUE)
R <- min(1,exp(mh1 - mh2))
if (R > runif(1)){phi <- phi.star}}

  # Save
  samples[k+1,] <- c(beta,sigma2.e,sigma2.alpha,phi)
  samples.alpha[k+1,] <- alpha
  accept[k+1,] <- ifelse(phi==phi.star,1,0)
  if(k%%1000==0) print(k)
}
    ## [1] 1000
## [1] 2000
## [1] 3000
## [1] 4000
## [1] 5000
## [1] 6000
## [1] 7000
## [1] 8000
## [1] 9000
## [1] 10000
    proc.time() - ptm
    ##    user  system elapsed 
##  18.591   1.490  20.114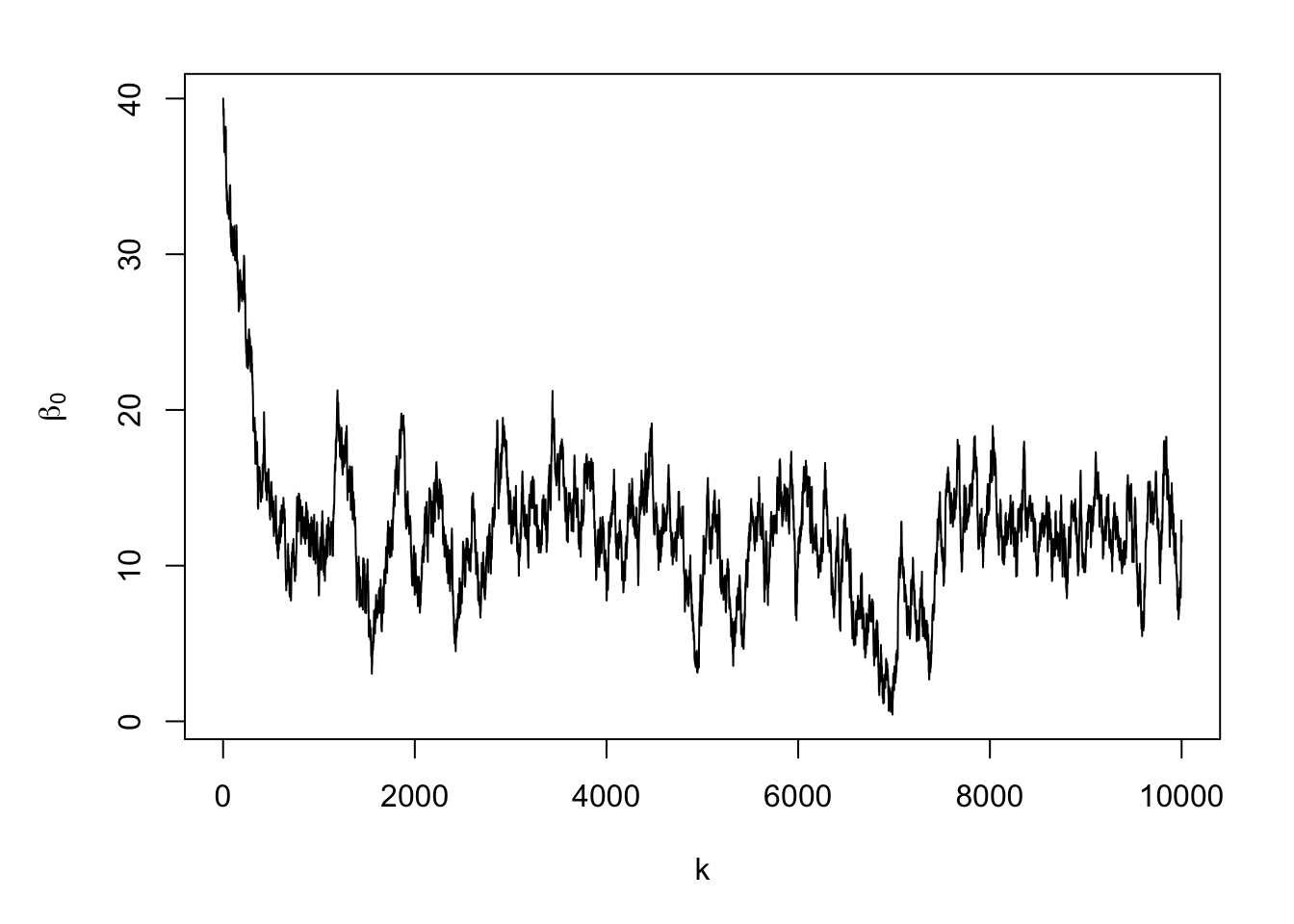
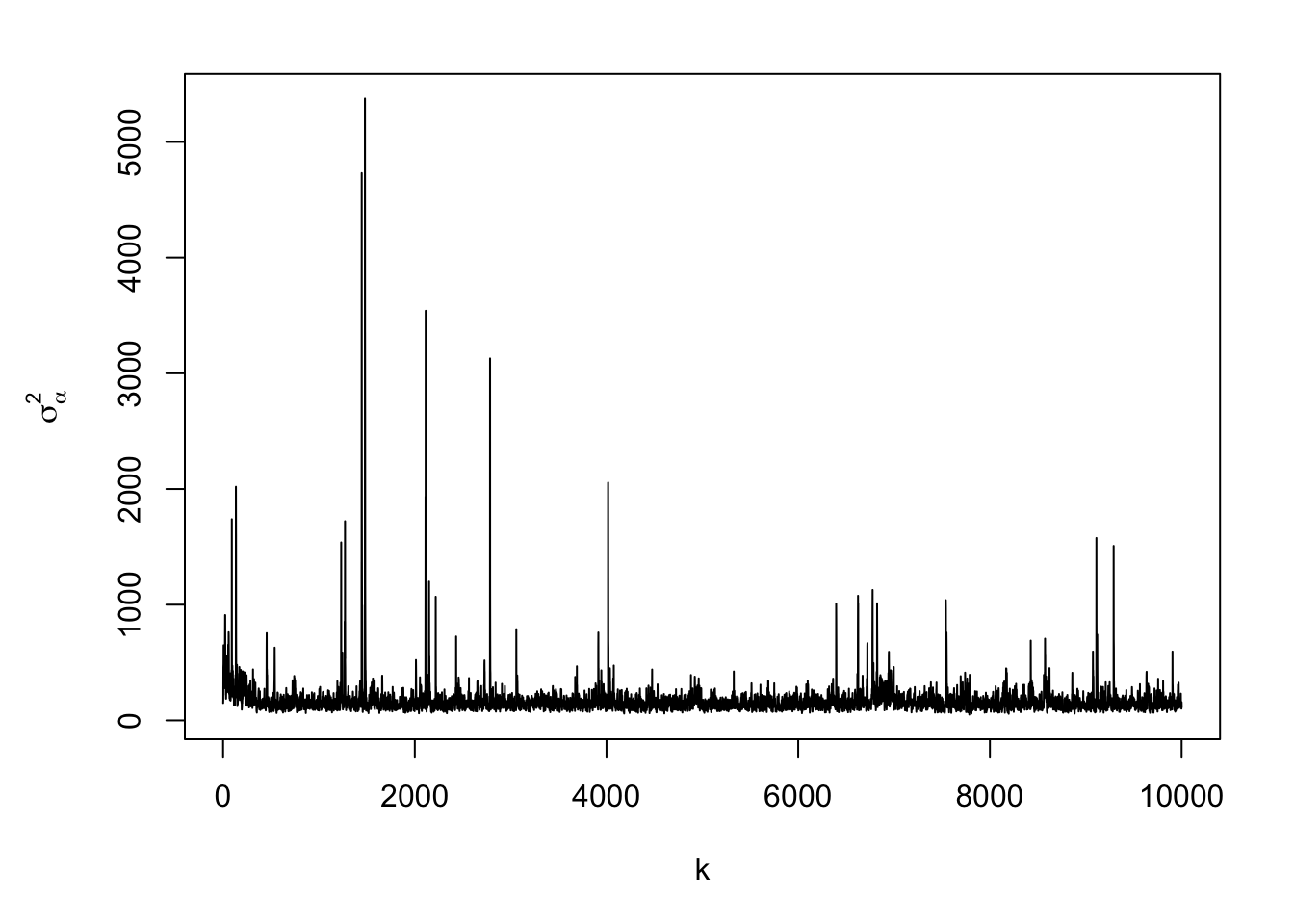
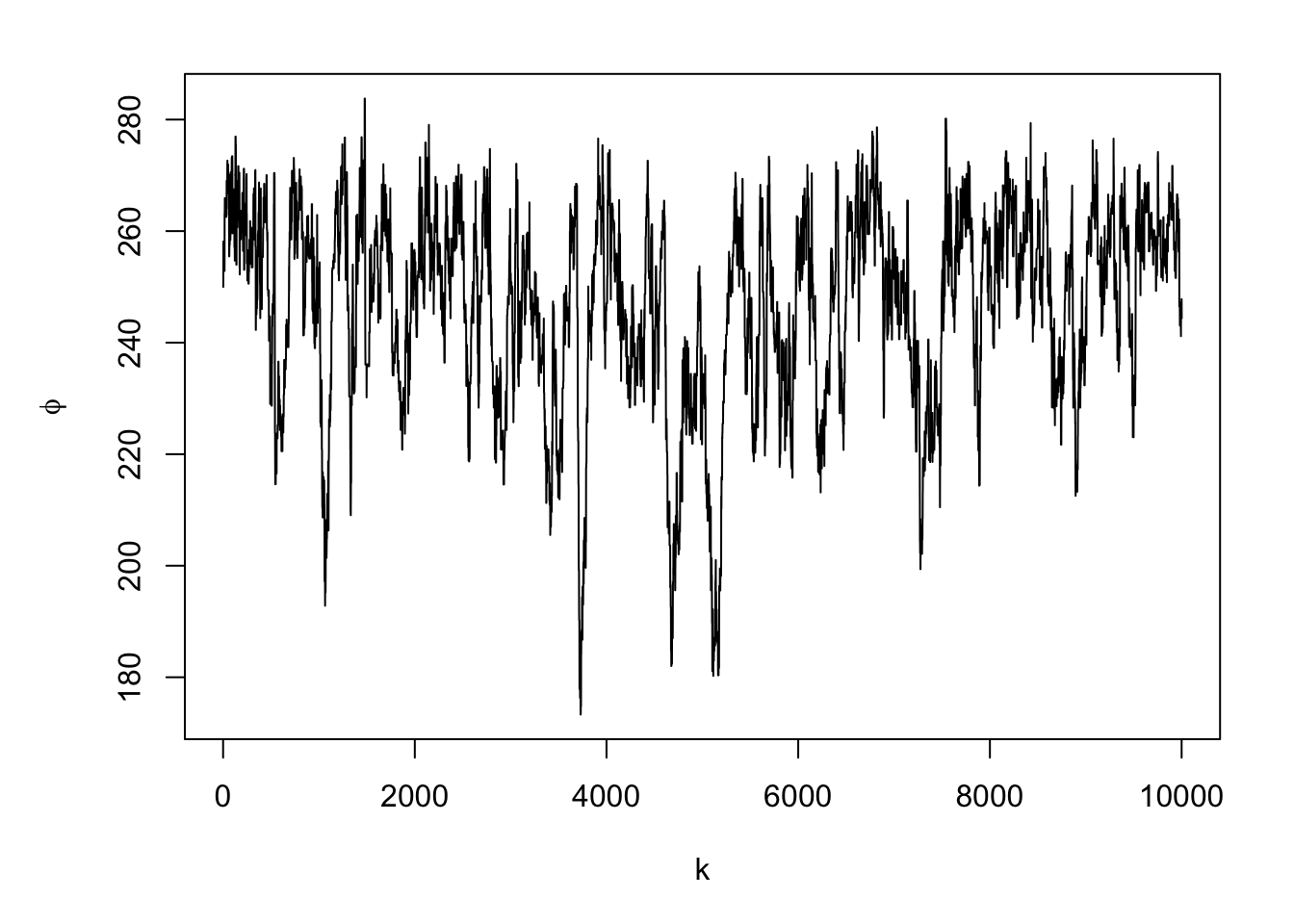
    mean(accept[-1,])
    ## [1] 0.3744
    par(mfrow=c(1,1),mar=c(5,5,2,2))
plot(samples[,1],typ="l",xlab="k",ylab=expression(beta[0]))

    plot(samples[,2],typ="l",xlab="k",ylab=expression(sigma[epsilon]^2))

    plot(samples[,3],typ="l",xlab="k",ylab=expression(sigma[alpha]^2))

    plot(samples[,4],typ="l",xlab="k",ylab=expression(phi))

    #Note: there is a trace plots for each of the 51 alphas
plot(samples.alpha[,1],typ="l",xlab="k",ylab=expression(alpha))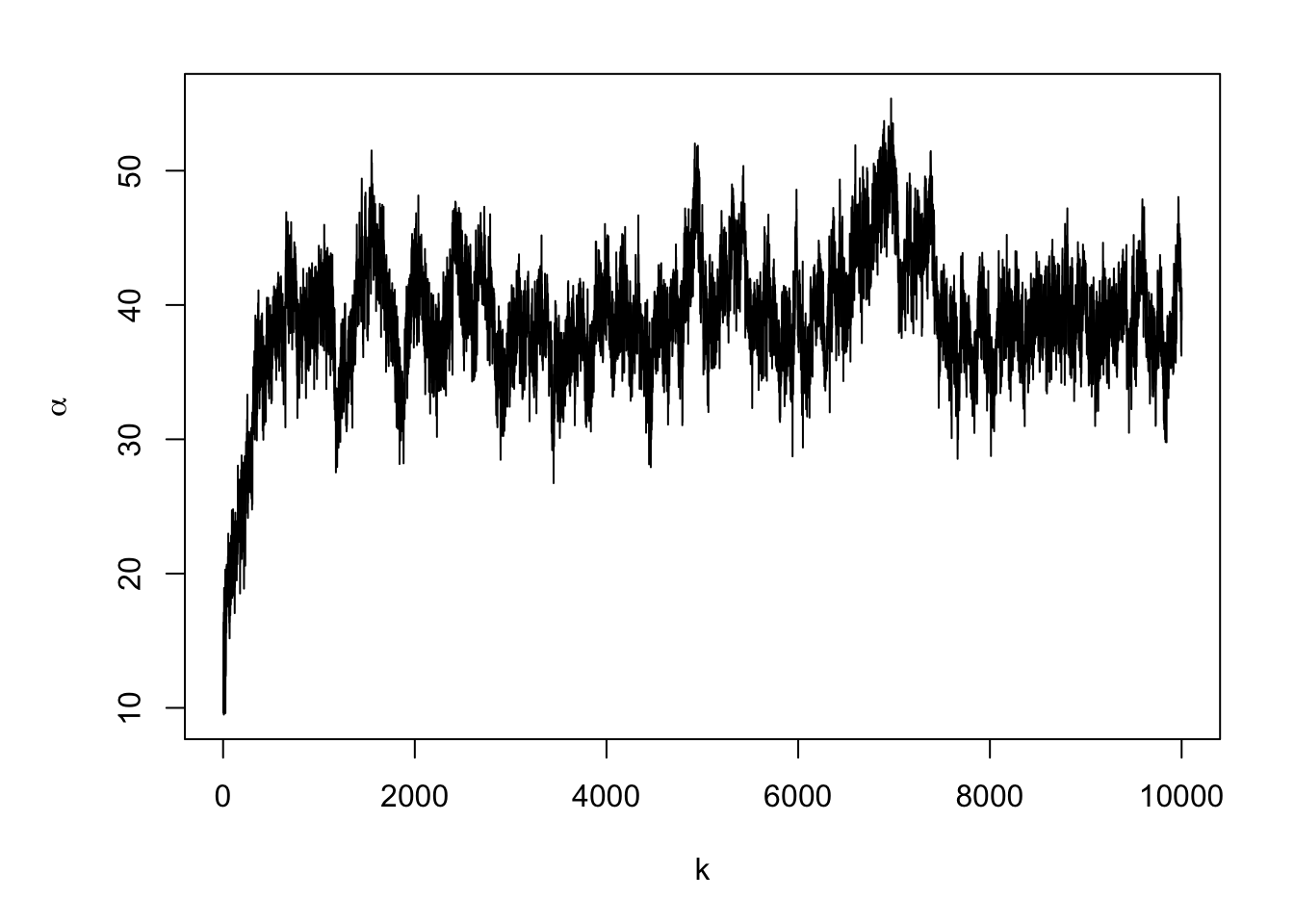

    burn.in <- 1000

#Effective sample size
effectiveSize(samples[-c(1:burn.in),])
    ## I(Depth/Depth)       sigma2.e   sigma2.alpha            phi 
##       39.51309     3283.46774      965.35201       58.74402
    effectiveSize(samples.alpha[-c(1:burn.in),])
    ##       V1       V2       V3       V4       V5       V6       V7       V8 
## 59.56160 49.82792 57.07751 48.99081 53.30777 43.70968 55.38660 45.69857 
##       V9      V10      V11      V12      V13      V14      V15      V16 
## 49.93532 47.14301 44.15401 53.99566 54.05355 45.99079 47.52021 45.34204 
##      V17      V18      V19      V20      V21      V22      V23      V24 
## 53.59280 49.23023 52.45801 46.94143 56.66246 53.20491 51.57685 47.47904 
##      V25      V26      V27      V28      V29      V30      V31      V32 
## 55.16787 47.17939 47.32656 50.79651 45.51036 48.02659 54.54050 47.49616 
##      V33      V34      V35      V36      V37      V38      V39      V40 
## 50.32102 53.67834 53.26875 45.94377 46.86828 54.00938 55.75524 48.21335 
##      V41      V42      V43      V44      V45      V46      V47      V48 
## 50.72585 53.72889 51.05043 47.42698 57.13272 43.55410 51.78176 52.50197 
##      V49      V50      V51 
## 48.57829 51.98884 49.18213
    # E() of beta, sigma2.e, sigma2.alpha, phi
colMeans(samples[-c(1:burn.in),])  
    ## I(Depth/Depth)       sigma2.e   sigma2.alpha            phi 
##      11.603376       5.129544     163.061302     245.726972
    # 95% Equal-tailed CIs
apply(samples[-c(1:burn.in),],2,FUN=quantile,prob=c(0.025,0.975)) 
    ##       I(Depth/Depth) sigma2.e sigma2.alpha      phi
## 2.5%        3.810371 3.003591     80.09624 201.3898
## 97.5%      17.776531 8.592822    335.24769 270.9082
    # obtain E(y) of at new depths
new.depth <- seq(min(df$Depth),max(df$Depth),by=10)
X.new <- model.matrix(~I(new.depth/new.depth)-1)
Z.new <- diag(1,length(new.depth))
D.cross <- rdist(new.depth,df$Depth)

samples.pred <- matrix(,length(burn.in:m.draws),length(new.depth))

for(k in burn.in:m.draws){
  alpha <- t(samples.alpha[k,])
  beta <- t(samples[k,1:dim(X)[2]])
  sigma2.e <- samples[k,dim(X)[2]+1]
  sigma2.alpha <- samples[k,dim(X)[2]+2]
  phi <- samples[k,dim(X)[2]+3]

  C <- exp(-(D/phi)^2) 
  C.cross <- exp(-(D.cross/phi)^2)

  alpha.new <- C.cross%*%solve(C)%*%alpha
  samples.pred[k-burn.in+1,] <- X.new%*%beta + Z.new%*%alpha.new
}


plot(df$Depth,df$Sources,las=1,ylim=c(0,60),col=rgb(0,0,0,0.25),pch=19,
 xlab="Depth (m)",ylab="Sources")
points(new.depth,colMeans(samples.pred),typ="l")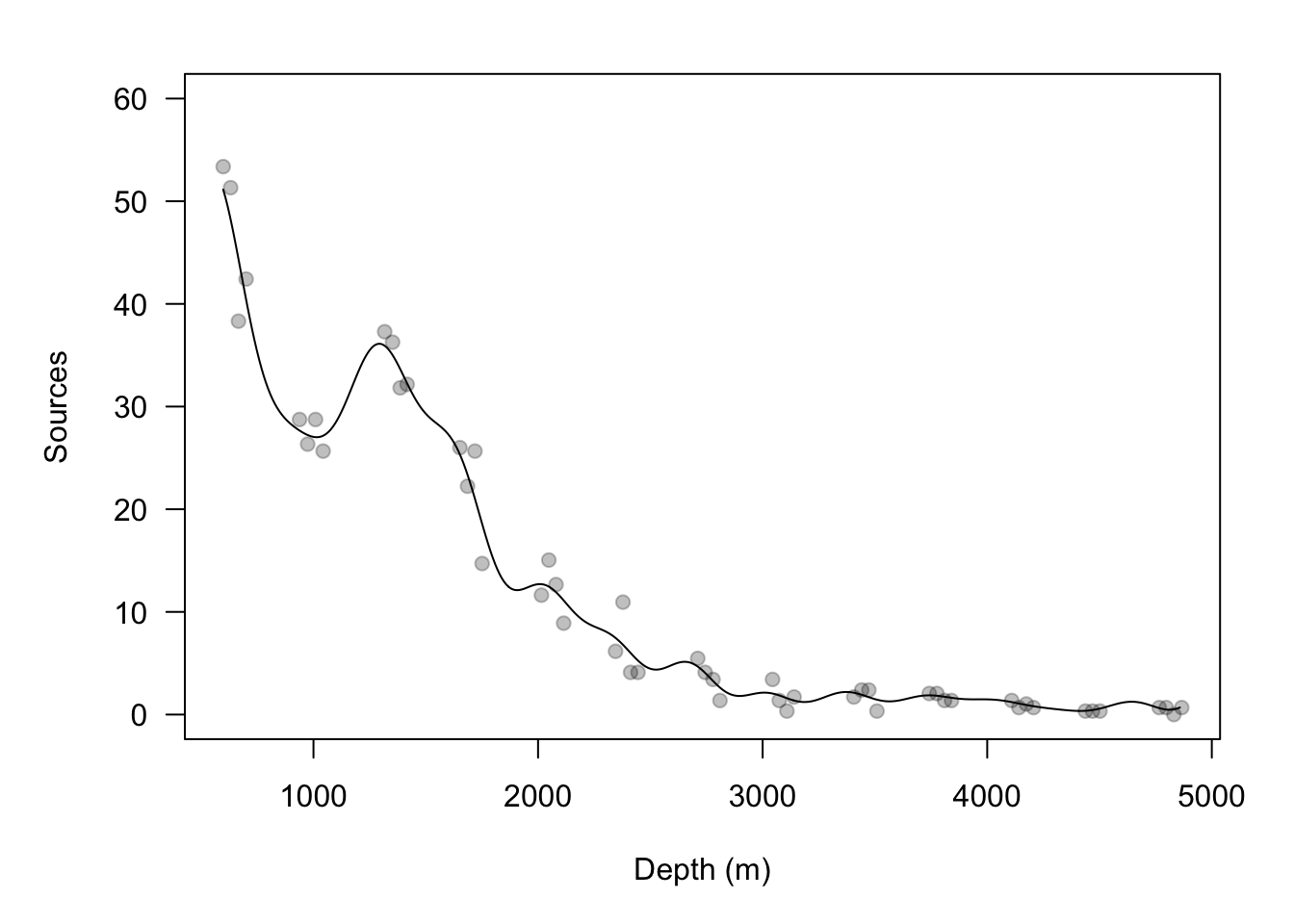

    EV.beta <- mean(samples[-c(1:burn.in),1])  
EV.alpha <- colMeans(samples.alpha[-c(1:burn.in),])
EV.e <- y - X%*%EV.beta - Z%*%EV.alpha 

par(mfrow=c(2,1))  
plot(df$Depth, EV.e, las = 1, col = rgb(0, 0, 0, 0.25),pch = 19, xlab = "Depth (m)", ylab = expression("E("*epsilon*")"))
hist(EV.e,col="grey",main="",breaks=10,xlab= expression("E("*epsilon*")"))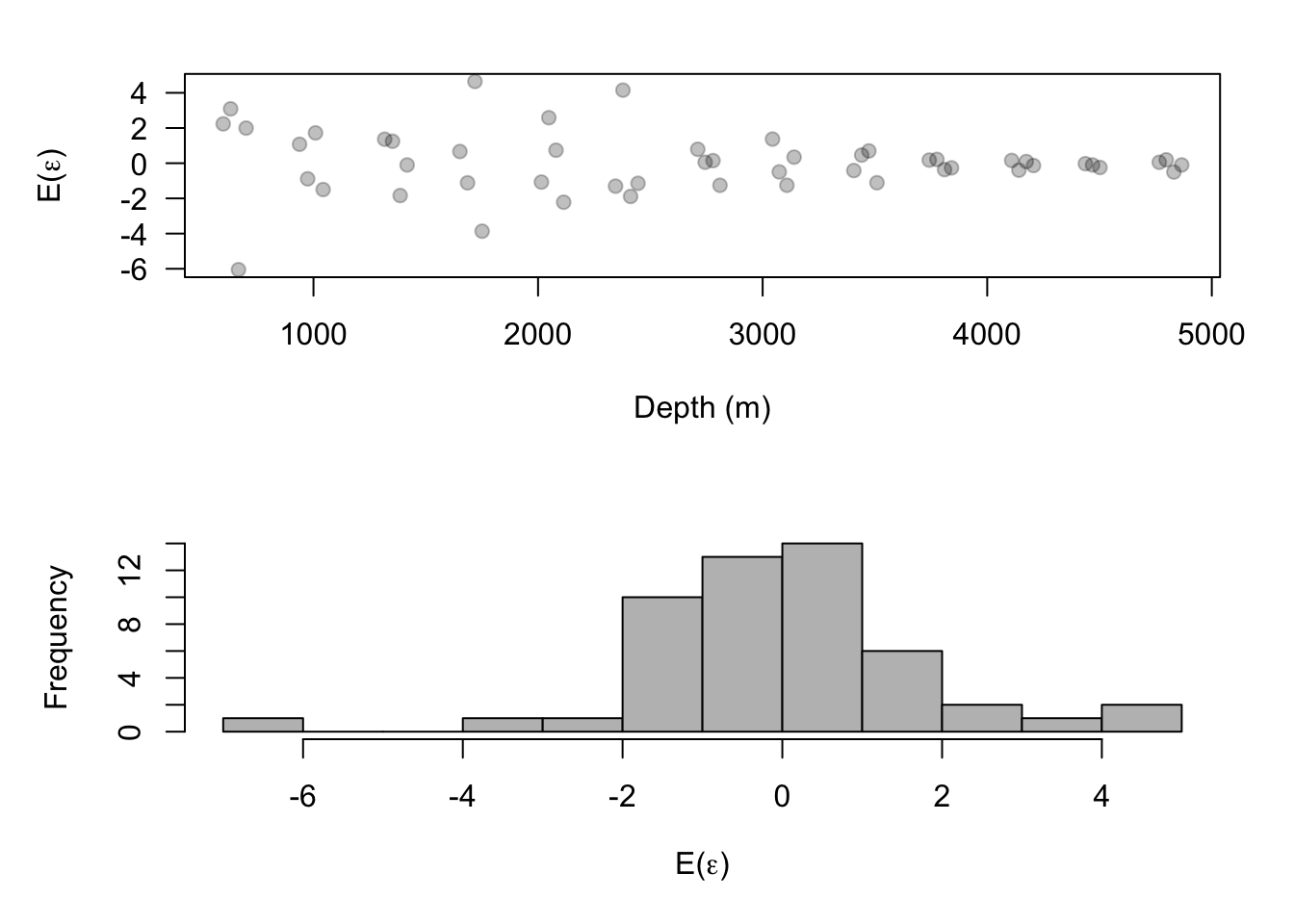

22.3 Extreme precipitation in Kansas