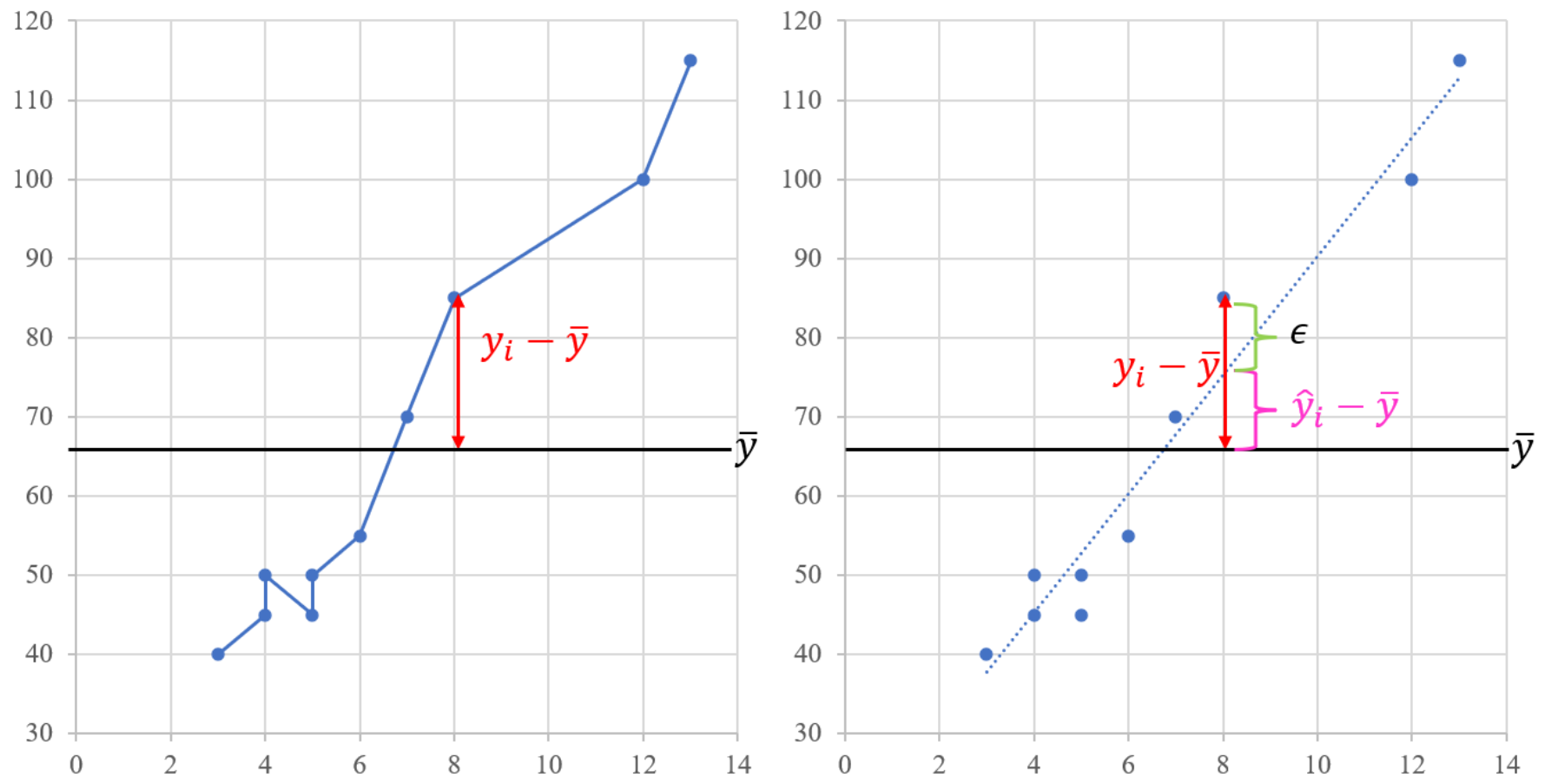
Likelihood ratio test (LRT) is one of the most popular test for model comparison in statistics, it is also the foundation of model fit evaluation in SEM.
What is likelihood ratio and likelihood ratio test
In statistics, just like other conventional statistical tests, i.e. t test, anova, LRT is used to test a hypothesis. LRT compares the goodness of fit of a null hypothesis model (h0 model, with less parameters) to that of an alternative model (h1 model, with more parameters). The h0 model is obtained by imposing some constraints over the h1 model (fix parameter at 0), and therefore nested in h1 model (i.e., h0 model is a special case of h1 model).
Suppose we have null hypothesis and alternative hypothesis as following:
- h0: the parameter \(\theta\) of underlying model is in the parameter space \(\Theta_0\),
- h1: the parameter \(\theta\) of underlying model is in the parameter space \(\Theta_0^\text{c}\),
where \(\Theta_0^\text{c}\) is the complement of \(\Theta_0\), the entire parameter space \(\Theta = \Theta_0 \cup \Theta_0^{\text{c}}\). The likelihood ratio is given by:
\[\text{LR} =\frac{~ \sup_{\theta \in \Theta_0} \mathcal{L}(\theta)=\mathcal{L}(\hat{\theta}_0)}{\sup_{\theta \in \Theta_o^{\text{c}}} \mathcal{L}(\theta)=\mathcal{L}(\hat{\theta}_1)}\]
where the \(\sup\) notation refers to the supremum and is realized through maximum likelihood estimation, thus \(\hat{\theta}\) represent the maximum likelihood estimator. As all likelihoods are positive, and as the constrained maximum cannot exceed the unconstrained maximum, the likelihood ratio is bounded between zero and one. Based on the ratio of their likelihoods. If the h0 model is true, the h1 model found by maximizing over the entire parameter space should be identical to the h0 model at population level, therefore the likelihood of h0 model should be very close to that of h1 model at sample level, the two likelihoods only differ by sampling error. Thus essentially, the likelihood-ratio test tests whether this ratio is significantly different from one.
Because \(\text{LR}\) is only a ratio and null hypothesis testing relies on an asymptotic sampling distribution of estimator, thus often the likelihood-ratio test statistic is expressed as :
\[\text{T}_\text{LR} =-2\ln(\text{LR})= -2 \left[\ell(\hat{\theta}_0) - \ell( \hat{\theta}_1) \right]\]
where \(\ell(\hat{\theta_0}) = \ln \left[\mathcal{L}(\hat{\theta}_0)\right],\ell( \hat{\theta}) = \ln \left[\mathcal{L}(\hat{\theta}_0)\right]\). \(\ell( \hat{\theta}_1)\)is the logarithm of the maximized likelihood function \(\mathcal{L}\) for sample data, and \(\ell(\hat{\theta}_0)\) is the maximal value in the special case that the null hypothesis is true (but not necessarily a value that maximizes \(\mathcal{L}\) for the sampled data). \(\hat{\theta}_0 \in \Theta_0\) and \(\hat{\theta}_1 \in \Theta_0^{\text{c}}\) denote the respective arguments of the maxima and the allowed ranges they’re embedded in. Multiplying by -2 ensures mathematically that \(\lambda_\text{LR}\) converges asymptotically (if \(n\) goes to infinity) to \(\chi^2\) distribution with degrees of freedom equal to the difference in dimensionality of \(\Theta_0^{\text{c}}\) and \(\Theta_0\), i.e. \(df = \#\text{par}_{h1}-\#\text{par}_{h0}\), if the null hypothesis happens to be true. If the resulting \(\hat{\lambda}_\text{LR}\) is larger than the critical value of \(\chi^2_{df}\), reject h0, otherwise do not reject h0.
The likelihood-ratio test requires that the models be nested. Two models are nested when one model is a special case of the other so that the special case model is considered a reduced model and the model in which the reduced model nested is the full model.
To conduct LRT, the key steps are: specifying h1 model and h0 model and count \(df\).
How to specify h1 model and h0 model?
LRT compares h0 model with h1 model. Normally, we use the best model as h1 model so that if our hypothezied one, h0 model, is true, \(L(\hat{\boldsymbol{\theta}}_1)>L(\hat{\boldsymbol{\theta}}_0)\) and the likelihood of these two model shall only differ slightly by sampling error. Here, best model corresponds to the most complex model available in the modeling framework we use to fit data. H0 model is obtained by imposing restrictions on the most complex model. The number of unknown parameters in h0 model decrease as well as its model complexity.
H0 model is also know as restricted model, whereas h1 model is also know as saturated model, or unrestricted model, due to the fact that it is the most complex model available for fitted data set. The concept of “most complex” could be approached from two different perspectives:
- Theoretical perspective.
This is a more general understanding of “complexity”. For example, given 3 \(x\)s and 1 \(y\), we can fit a multiple regression \[y=\beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_3+\epsilon,\] we can also fit a multiple regression with all 3 2nd order interaction effects \[y=\beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_3+\beta_4x_1x_2+\beta_5x_1x_3+\beta_6x_2x_3+\epsilon.\] The latter one is clearly more complex than the former model. However, given this 4 variables scenario, we can actually have a wide variety of choices in terms of complex model. For example, we can fit a even more complex model with non-linear effect \[y=\beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_3+\beta_4x_1x_2+\beta_5x_1x_3+\beta_6x_2x_3+\beta_7x_1^2+\epsilon.\] With so many complex models available, researchers must base their decision on theory, thus the “complexity” of model is purely a theory-driven concept.
- Statistical perspective.
This is an understanding that is specific to LRT. The “complexity” of model is capped by the number of variables used, where “variable” refers to background variable in the right hand side of regression model, or column of non-dependent-variable in data set. For example, if we have 3 \(x\)s and 1 \(y\), we decide to fit a model (h0 model) with all interaction effects \[\begin{align*}
y &=\beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_3+\\
&\quad \enspace \beta_4x_1x_2+\beta_5x_1x_3+\beta_6x_2x_3+\\
&\quad \enspace \beta_7x_1x_2x_3+\\
&\quad \enspace \epsilon.
\end{align*}\] In this case, we have 7 background variables (\(x_1\), \(x_2\), \(x_3\), \(x_1x_2\), \(x_1x_3\), \(x_2x_3\), \(x_1x_2x_3\)) in the right hand side of the model above, 7 columns of non-dependent variables in the data sets to which the model is fitted. We can not increase the complexity of model without adding new background variable to the right hand side of model above or new column into the data set (i.e. add \(x_1^2\)). Thus for LRT, the most complex model in this case is the same model above, that is, h1=h0.
Likewise, it is easy to see that if we decide to fit \[y=\beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_3+\epsilon,\] which is the h0 model, the number of background variables or the number of non-dependent-variable columns is 3. The most complex model available is h0 itself, therefore h1=h0.
What if we want to fit a h0 with less parameter than h1? Suppose we have 2 \(x\)s and 1 \(y\), we decide to use a linear regression without interaction effect (h0 model) \[y_i=\beta_0+\beta_{1}x_{1i}+\beta_{2}x_{2i}+\epsilon_i.\] Then the h1 model is also the h0 model. If we assumed that \(x_2\) has no effect on \(y\), we can fix the slope of \(x_2\) at 0, the resulting h0 model is \[y_i=\beta_0+\beta_{1}x_{1i}+0x_{2i}+\epsilon_i,\] not \[y_i=\beta_0+\beta_{1}x_{1i}+\epsilon_i.\] In this case, there are still 2 background variables or 2 columns of non-dependent variables in data set. Thus the h1 model remains unchanged, the h0 model becomes a smaller one.
Other examples:
Coding session
Assume we have a linear regression model with fixed \(x\)s as \[y_i=\beta_0+\beta_1x_{1i}+\beta_2x_{2i}+\beta_3x_{3i}+\epsilon_i,\]
In this scenario, we can have the following models available for testing:
- m1: \(y=\beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_3+\epsilon_i\),
- m2: \(y=\beta_0+\beta_1x_1+\beta_2x_2+0x_3+\epsilon_i\)
- m3: \(y=\beta_0+\beta_1x_1+0x_2+0x_3+\epsilon_i\)
Task 1
Data generation model is m2 and: \(\beta_0=\beta_1=\beta_2=1\), \(\beta_3=0\), \(\epsilon_i\in N(0,1)\).
- Generate data from this model with sample size \(n=1000\),
- Fit m1, m2, and m3 using Mplus (the equivalent R function
lm() in R) separately,
- Conduct LRT using Mplus to compare m2 (h0) with m1 (h1), m3 (h0) with m1 (h1), and m3 (h0) with m2 (h1), record the resulting p-value (the equivalent R function is
lmtest::lrtest(),
- Replicate steps 1-3 100 times, count the number of p-value < .05 (R learner only).
For non-quant students, do steps 2-3 using “1y 3xs no interaction.txt”.
Task 2
Data generation model is m3: \(\beta_0=\beta_1=1\), \(\beta_2=\beta_3=0\), \(\epsilon_i\in N(0,1)\). Repeat steps 1-4.
For non-quant students, do steps 2-3 using “1y 3x 2ind_x no interaction.txt”.
Task 3
Assume we have the following linear regression model with fixed \(x\)s as data generation model \[\begin{align*}
y_i&=\beta_0+\beta_1x_{1i}+\beta_2x_{2i}+\beta_3x_{3i}+\\
&\quad \enspace \beta_4x_{1i}x_{2i}+\beta_5x_{1i}x_{3i}+\beta_6x_{2i}x_{3i}+\\
&\quad \enspace \beta_7x_{1i}x_{2i}x_{3i}+\\
&\quad \enspace \epsilon_i,
\end{align*}\] where \(\beta_0=\beta_1=\beta_2=\beta_3=\beta_4=\beta_7=1\), \(\beta_5=\beta_6=0\), \(\epsilon_i\in N(0,1)\).
In this scenario, we can have the following models available for testing:
- m1, with all 2nd and 3rd order interaction effects:
\[\begin{align*}
y_i&=\beta_0+\beta_1x_{1i}+\beta_2x_{2i}+\beta_3x_{3i}+\\
&\quad \enspace \beta_4x_{1i}x_{2i}+\beta_5x_{1i}x_{3i}+\beta_6x_{2i}x_{3i}+\\
&\quad \enspace \beta_7x_{1i}x_{2i}x_{3i}+\\
&\quad \enspace \epsilon_i,
\end{align*}\]
- m2, remove 2 2nd order interaction effects:
\[\begin{align*}
y_i&=\beta_0+\beta_1x_{1i}+\beta_2x_{2i}+\beta_3x_{3i}+\\
&\quad \enspace \beta_4x_{1i}x_{2i}+0x_{1i}x_{3i}+0x_{2i}x_{3i}+\\
&\quad \enspace \beta_7x_{1i}x_{2i}x_{3i}+\\
&\quad \enspace \epsilon_i,
\end{align*}\]
- m3, all 3 2nd order interaction effects, no 3rd order interaction effect:
\[\begin{align*}
y_i&=\beta_0+\beta_1x_{1i}+\beta_2x_{2i}+\beta_3x_{3i}+\\
&\quad \enspace \beta_4x_{1i}x_{2i}+\beta_5x_{1i}x_{3i}+\beta_6x_{2i}x_{3i}+\\
&\quad \enspace 0x_{1i}x_{2i}x_{3i}+\\
&\quad \enspace \epsilon_i,
\end{align*}\]
\[\begin{align*}
y_i&=\beta_0+\beta_1x_{1i}+\beta_2x_{2i}+\beta_3x_{3i}+\\
&\quad \enspace 0 x_{1i}x_{2i}+ 0 x_{1i}x_{3i}+ 0 x_{2i}x_{3i}+\\
&\quad \enspace 0 x_{1i}x_{2i}x_{3i}+\\
&\quad \enspace \epsilon_i,
\end{align*}\]
- Generate data from this model with sample size \(n=1000\),
- Fit m1, m2, and m3 using Mplus (the equivalent R function
lm() in R) separately,
- Conduct LRT using Mplus to compare m2 (h0) with m1 (h1), m3 (h0) with m1 (h1), and m4 (h0) with m1 (h1), record the resulting p-value (the equivalent R function is
lmtest::lrtest()),
- Replicate steps 1-3 100 times, count the number of p-value < .05 (R learner only).
For non-quant students, do steps 2-3 using “1y 3xs interaction.txt”.
Model misspecification
LRT is able to detect model misspecification of h0 model only when:
- h1 model is correctly specified,
- h0 is nested in h1.
There are basically three types of model misspecifications.
- Parameter-level misspecification
- non-existing parameter being estimated freely: h0 model has superfluous parameter of which the population value is 0 (e.g. true model is m3 but fit model is m2);
- existing non-zero parameter being fixed (usually at 0): h0 model lacks parameter of which the population value is non-zero (e.g. true model is m2 but fit model is m3).
For the first type of parameter-level misspecification, LRT shall endorse the h0 model with superfluous parameters by generating a p-value > 0.05, because 0 is within the parameter space of h0 when freely estimated. In this case, if we continued to fix superfluous parameter at 0 to obtain a new smaller h0 model, then LRT shall endorse this new h0 model without superfluous parameter as well.
For the second type of parameter-level misspecification, LRT shall reject the h0 model by generating a p-value < 0.05, because when fixing an existing parameter at 0, the parameter space of this specific parameter is 0 and does not include the true value (non-zero), h0 is false.
- Function-level misspecification:
The regression relationship between two variables is not linear, but a linear regression is used to fit the data. \[\begin{align*}
\text{True model: }y=f(x)&=\beta_0+\beta_1x^2,\\
\text{Fitting model: }y&=\beta_0+\beta_1x.
\end{align*}\]
Function-level misspecification usually leads to non-nest models and is beyond the capability of LRT. Because normally we fit linear model to data, h0 and h1 model shall all be linear. Thus there will be model misspecification in both h0 and h1 models, the asymptotic distribution of LRT test statistic will be violated.
- Distribution-level misspecification
In general, if we use maximum likelihood, we assume to have normally distributed data. However, this distributional assumption may not be hold in real data. If violated, even if we fit the true model using normal-based ML, we shall still have biased parameter estimation. Therefore distribution-level misspecification is always beyond LRT.