Rozdział 4 Dobry i zły klient
4.1 Zaniechanie spłaty (default)
W przypadku scoringu kredytowego jako złego klienta można traktować takiego, który zaniechał spłaty (ang. default — zaniechanie). W praktyce default może oznaczać, przykładowo, opóźnienie w spłacie większe niż 90 dni w ciągu pierwszych dwunastu miesięcy roku po uruchomieniu kredytu.
4.2 Szkodowość
Zaniechanie spłaty (default) rozpoznajemy najczęściej po opóźnieniu w spłacie. Typowy sposób liczenia opóźnienia to opóźnienie w dniach (skrót DPD, days past due oznacza dni opóźnienia). Opóźnianie się w spłacie nazywane jest czasem szkodowością (ang. delinquency). Typowe poziomy opóźnienia to 30, 60, 90, 120 dni (wielokrotności trzydziestki, czyli w przybliżeniu pełne miesiące). O ile określenia default używa się w przypadku dużych opóźnień (90 dni), o tyle scoring kredytowy może być budowany na podstawie niższych poziomów szkodowości, np. opóźnień 30-dniowych.
Stąd też w przypadku definicji zmiennej celu w modelu scoringowych mówi się często nie o obserwacjach default, ale o obserwacjach złych (bad) i dobrych (good). Zadaniem w modelu scoringowego jest więc utworzenie rankingu klientów, kredytów, wniosków kredytowych według prawdopodobieństwa złego lub dobrego. Scoring kredytowy będzie działał dobrze, jeżeli częstość złych (ang. bad rate) będzie wyższa dla obserwacji z niższą oceną punktową, a niższa dla obserwacji o wysokiej ocenie.
4.3 Szansa, log-odds
Zamiast częstości lub prawdopodobieństwa złego stosuje się czasem szansę (ang. odds) lub logarytm naturalny szansy (ang. log-odds).
Jeżeli prawdopodobieństwo (lub częstość) złego dla danej obserwacji lub grupy obserwacji oznaczymy symbolem \(p_B\), a prawdopodobieństwo dobrego symbolem \(p_G\), gdzie \(p_G = 1 - p_B\), to szanse złego i dobrego dla tej samej obserwacji/grupy (\(s_B\) i \(s_G\)) możemy zdefiniować następująco:
\[s_B = \frac{p_B}{1-p_B}=\frac{p_B}{p_G}; \qquad s_G = \frac{p_G}{1-p_G}=\frac{p_G}{p_B}\]
Warto zauważyć, że szansa złego do odwrotność szansy dobrego:
\[s_B = \frac{1}{s_G}\] Przekształcenie odwrotne, z szansy na prawdopodobieństwo wygląda następująco:
\[p_B = \frac{s_B}{s_B+1} = \frac{1}{1+s_G} \qquad p_G = \frac{s_G}{s_G+1} = \frac{1}{1+s_B}\]
Prawdopodobieństwa przyjmują wartości z przedziału \([0; 1]\), odpowiadające im szanse przyjmuja wartości z przedziału \([0; +\infty)\)
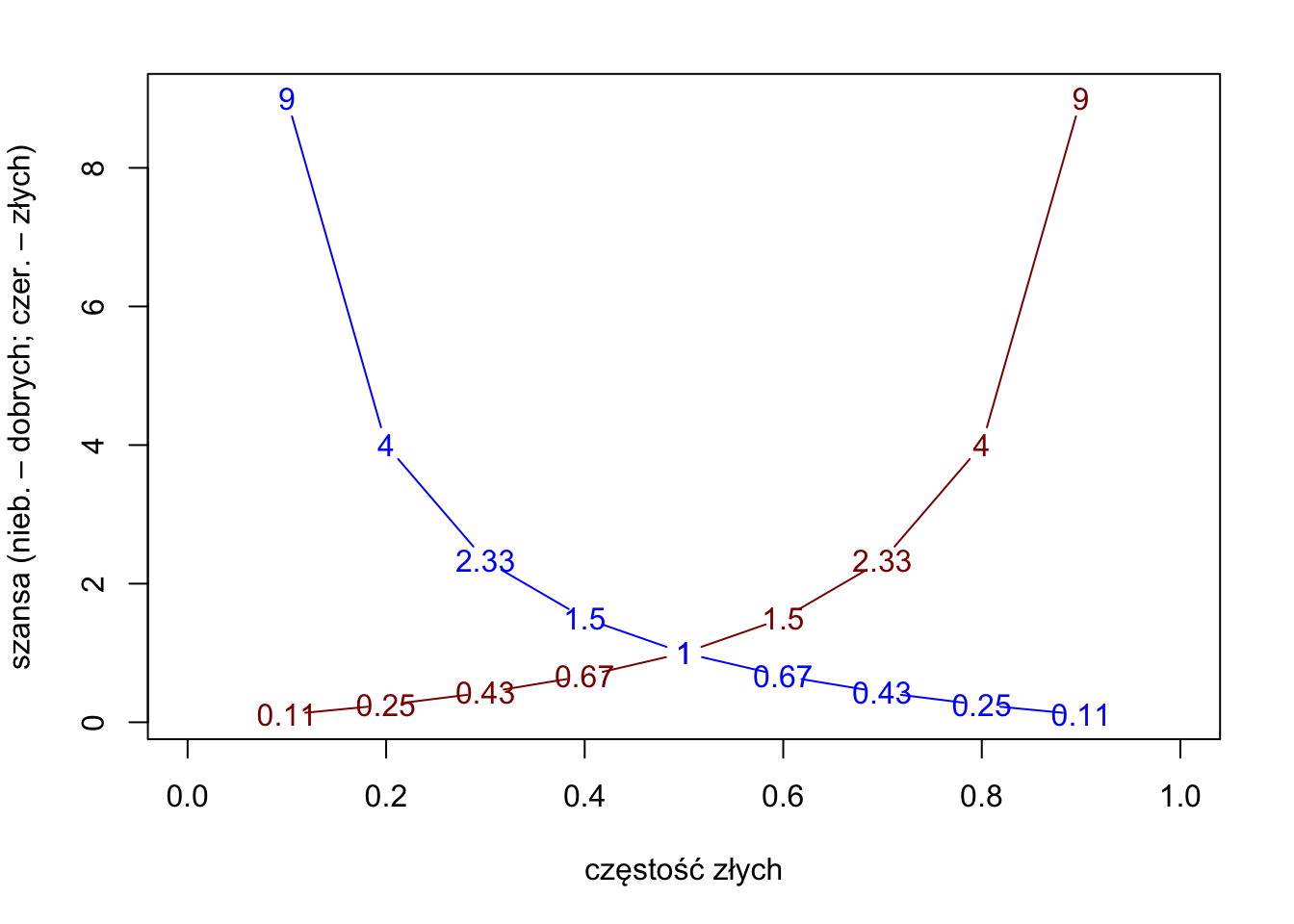
Rysunek 4.1: Prawdopodobieństwa z przedziału (0,1) i odpowiadające im szanse.
Czasem (np. w przypadku regresji logistycznej) używa się logarytmów szans (log-odds):
\[l_B = \ln{s_B} = \ln\frac{p_B}{1-p_B} = \ln\frac{p_B}{p_G}\]
Funkcję \(f(x)=\ln\frac{x}{1-x}\) nazywa się funkcją logitową.
Odwrotne przekształcenia wyglądają tak2:
\[s_B = \exp(l_B)\]
\[p_B = \frac{\exp(l_B)}{1+\exp(l_B)} = \frac{1}{1+\exp(-l_B)} \]
Funkcję \(f(x) = \frac{1}{1+\exp(-x)}\) nazywa się funkcją logistyczną.
Prawdopodobieństwa przyjmują wartości z przedziału \([0; 1]\), odpowiadające im szanse przyjmuja wartości z przedziału \((-\infty; +\infty)\)
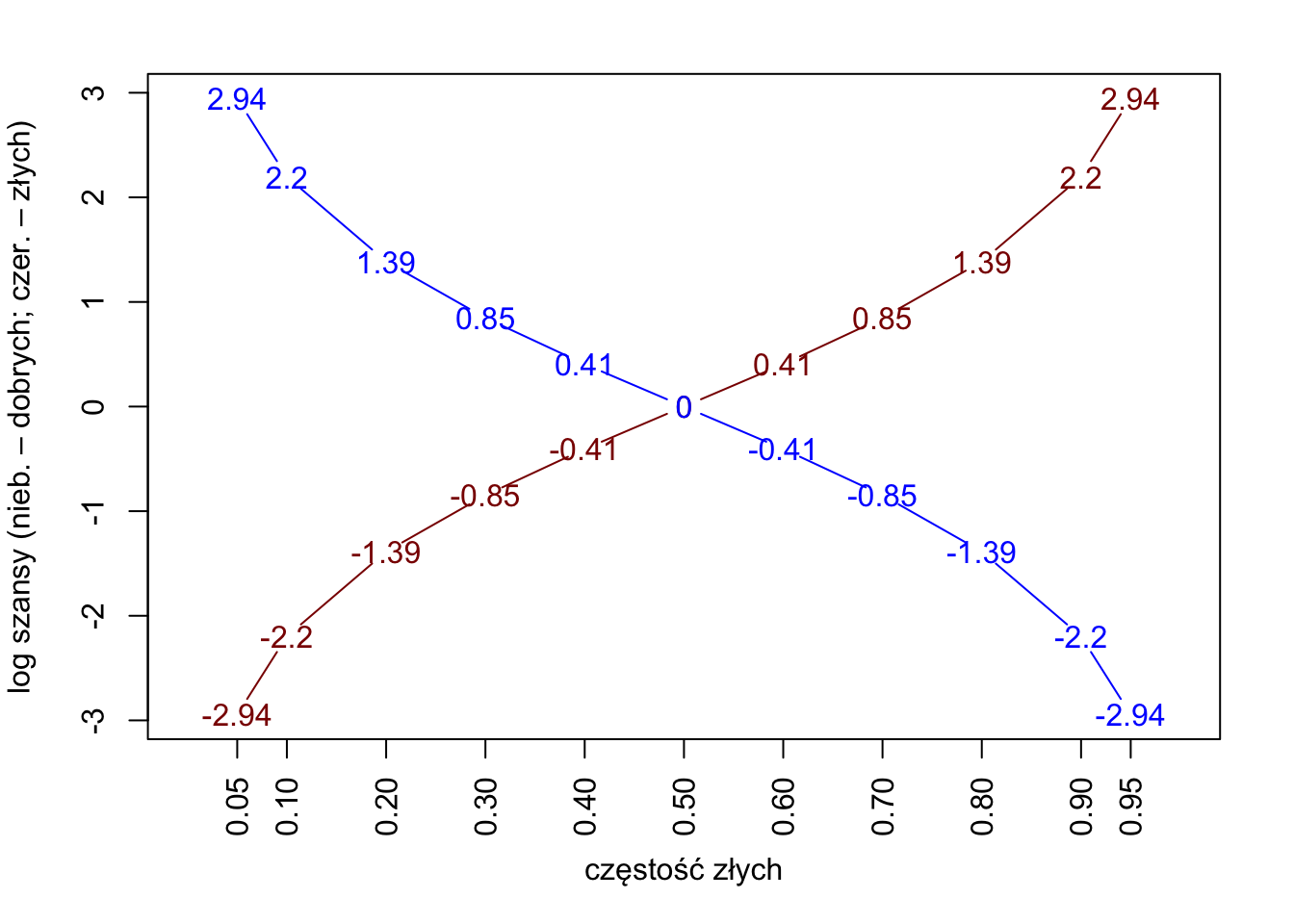
Rysunek 4.2: Prawdopodobieństwa z przedziału (0,1) i odpowiadające im logarytmy szans.
zapis \(\exp(x)\) oznacza \(e^x\)↩︎