Rozdział 3 Ocena jakości bankowych modeli scoringowych
3.1 Tablica pomyłek
Tablica pomyłek pozwala ocenić skuteczność binarnego algorytmu klasyfikującego, czyli takiego, który przypisuje obiekt do jednej z dwóch klas. Jedną z tych dwóch klas zwykle nazywa się klasą pozytywną albo dodatnią (oznacza się ją symbolem „+” lub wartością 1), zaś drugą z klas negatywną albo ujemną (oznaczana sybolem „-” lub wartością 0).
3.1.1 Przykład tablicy pomyłek:
| Klasa przewidywana: pozytywna | Klasa przewidywana: negatywna | Razem | |
|---|---|---|---|
| Klasa rzeczywista: pozytywna | 39 | 14 | 53 |
| Klasa rzeczywista: negatywna | 28 | 156 | 184 |
| Razem | 67 | 170 | 237 |
Jest to tabela o wymiarach 2×2, pokazująca ile przypadków znalazło się w każdej kombinacji rzeczywistej i przewidywanej klasy1. Pozwala ona ocenić, jak często algorytm trafiał lub się mylił w przypisywaniu klas.
3.1.2 Miary oparte na tablicy pomyłek
Najprostszą miarą jakości klasyfikacji jest dokładność. Jest to udział obserwacji z prawidłowo przewidzianą klasą we wszystkich obserwacjach.
Przykład 3.1 Na podstawie powyższej tabeli można stwierdzić, że algorytm dokonał poprawnej klasyfikacji w 39 + 156 = 195 przypadkach. Ponieważ łącznie obserwacji było 237, dokładność wyniosła 195/237, czyli 82,3%.
W praktyce modeli scoringowych (ale także na przykład w przypadku statystyki medycznej) popularne są dwie inne miary: czułość i swoistość. Czułość to udział poprawnych klasyfikacji wśród obserwacji rzeczywiście pozytywnych, zaś swoistość to udział poprawnych klasyfikacji wśród obserwacji rzeczywiście negatywnych.
Przykład 3.2 Dane w powyższej tabeli pozwalają stwierdzić, że rzeczywistych obserwacji pozytywnych było 39 + 14 = 53. Spośród nich prawidłowo sklasyfikowano 39, co oznacza, że czułość wyniosła 39/53, czyli 73,6%. Obserwacji rzeczywiście negatywnych było 28 + 156 = 184. Spośród nich prawidłowo sklasyfikowano 156, co oznacza, że swoistość wyniosła 156/184, czyli 84,8%.
Wzory na dokładność, czułość i swoistość można zapisać, stosując typowe oznaczenia liczebności komórek w tablicy pomyłek:
TP (true positives) to obserwacje prawdziwie pozytywne, czyli takie, których zarówno rzeczywista, jak i przewidywana klasa jest pozytywna
TN (true negatives) to obserwacje prawdziwie negatywne, czyli poprawnie zaklasyfikowane obserwacje z klasy negatywnej
FP (false positives) to obserwacje fałszywie pozytywne, czyli obserwacje błędnie zaklasyfikowane jako pozytywne (w rzeczywistości negatywne)
FN (false negatives) to obserwacje fałszywie negatywne, czyli obserwacje błędnie zaklasyfikowane jako negatywne (w rzeczywistości pozytywne).
Wtedy:
\[ \text{Dokładność} = \frac{TP+TN}{TP+TN+FP+FN}, \tag{3.1} \]
\[ \text{Czułość} = \text{TPR} = \frac{TP}{TP+FN}, \tag{3.2} \] \[ \text{Swoistość} = \frac{TN}{TN+FP}, \tag{3.3} \]
Czułość nazywana jest również frakcją wyników prawdziwie pozytywnych (ang. true positive rate, TPR). Z kolei frakcja wyników fałszywie pozytywnych (ang. false positive rate, FPR) to jeden minus swoistość.
\[ \text{FPR} = 1 - \text{Swoistość} = \frac{FP}{TN+FP}, \tag{3.4} \]
Zaproponowano wiele miar opartych na tablicy pomyłek, innych niż dokładność, czułość i swoistość. Wiele z nich można znaleźć w przygotowanym szablonie (Arkuszu Google).
3.1.3 Tablica pomyłek dla modelu scoringowego
Żeby zbudować tablicę pomyłek dla modelu scoringowego, należy:
- określić, która z dwóch klas będzie traktowana jako pozytywna, a która jako negatywna
oraz
- ustalić cut-off, czyli punkt odcięcia, nazywany też progiem decyzyjnym (ang. threshold); jest to wartość oceny punktowej stanowiąca granicę pomiędzy przewidywaną klasą pozytywną i negatywną.
W przypadku scoringu kredytowego za klasę pozytywną zwyczajowo uznaje się kredyty złe, czyli te, które nie są spłacane. Choć może to być nieintuicyjne (bo „pozytywny” kojarzy się z czymś dobrym), jest to zgodne z praktyką stosowaną w innych dziedzinach, takich jak diagnostyka medyczna (gdzie wynik pozytywny oznacza wykrycie choroby) czy systemy wczesnego ostrzegania (np. przewidywanie tornad lub awarii). W przypadku niektórych innych bankowych modeli scoringowych klasa pozytywna może rzeczywiście oznaczać coś pożądanego, tak może być w przypadku response scoring, czyli modelu przewidującego, czy klient skorzysta z oferty kredytowej.
W niektórych sytuacjach wiemy, że interesuje nas jeden konkretny punkt odcięcia (np. „klientów ze scoringiem poniżej 550 nie akceptujemy”). Zwykle jednak, jak zobaczymy niżej, buduje się miary oparte na tablicach pomyłek wyznaczonych dla wielu poziomów cut-off.
Warto zauważyć, że bankowy model scoringowy sam w sobie nie jest binarnym algorytmem klasyfikującym – nie przypisuje obserwacji bezpośrednio do jednej z dwóch klas. Zamiast tego zwraca ocenę punktową, zwykle powiązaną z prawdopodobieństwem wystąpienia określonego zdarzenia (np. braku spłaty). Dopiero w połączeniu z ustalonym punktem odcięcia model scoringowy może pełnić funkcję klasyfikatora binarnego – i dopiero wtedy możliwe jest zastosowanie tablicy pomyłek do oceny jego skuteczności.
3.2 Krzywa ROC
Krzywa ROC (krzywa charakterystyki operacyjnej odbiornika, ang. receiver operating characteristic curve) to wykres, który powstanie poprzez połączenie punktów o współrzędnych odpowiadających wartościom FPR (na osi x) oraz TPR (na osi y) dla wszystkich możliwych poziomów odcięcia.
Przykład 3.3 Załóżmy, że model ratingowy zalicza wnioskujących o kredyt do czterech grup. 1. grupa charakteryzuje się największym ryzykiem kredytowym, 4. – najniższym. Tym samym możliwe są następujące poziomy odcięcia: (1) odcięcie grupy 1, (2) odcięcie grup 1 i 2, (3) odcięcie grupy 1, 2 i 3. Dodatkowo teoretycznie możliwe są dwa poziomy skrajne: nie odcinamy nikogo lub odcinamy wszystkie grupy. Czułość (udział obserwacji odciętych wśród obserwacji rzeczywiście pozytywnych, czyli klientów niespłacających) i swoistość (udział obserwacji odciętych wśród w rzeczywistości negatywnych, czyli wśród klientów spłacających) przedstawiono w następującej tabeli:
| cut off | czułość (TPR) | swoistość (FPR) |
|---|---|---|
| 1 | 0,60 | 0,90 |
| 2 | 0,80 | 0,80 |
| 3 | 0,95 | 0,60 |
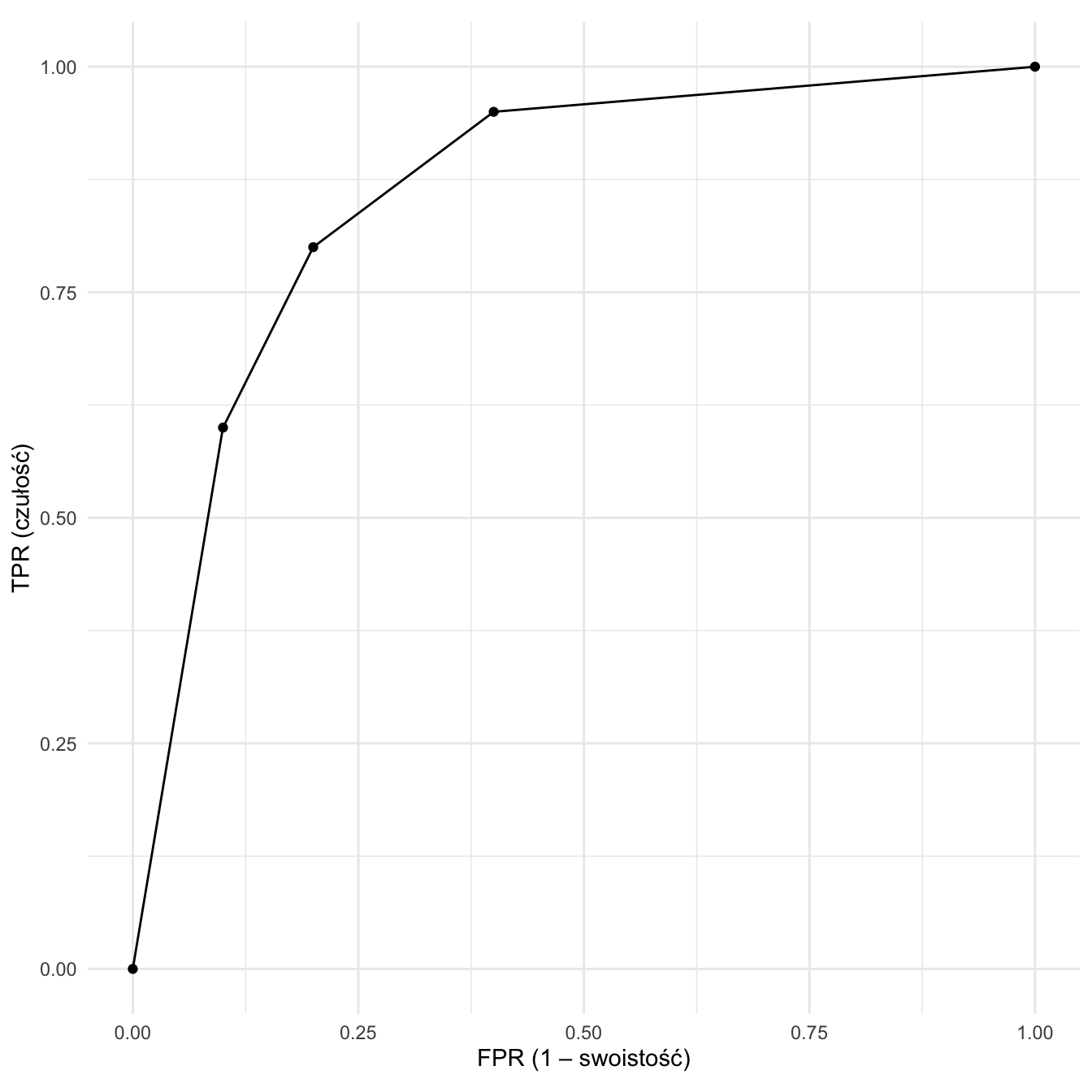
Rysunek 3.1: Krzywa ROC
Punkty (0; 0) i (1; 1) reprezentują skrajne poziomy odcięcia. Zawiera je z definicji każda krzywa ROC.
3.3 AUC i współczynnik Giniego
AUC (ang. area under (the) curve) albo AUROC (ang. area under (the) ROC) to pole pod krzywą ROC. AUC jest więc miarą siły dyskryminacyjnej modelu scoringowego. Krzywa ROC składa się punktów przedstawiających czułość i swoistość dla różnych poziomów odcięcia, zaś AUC podsumowuje przebieg tej krzywej.
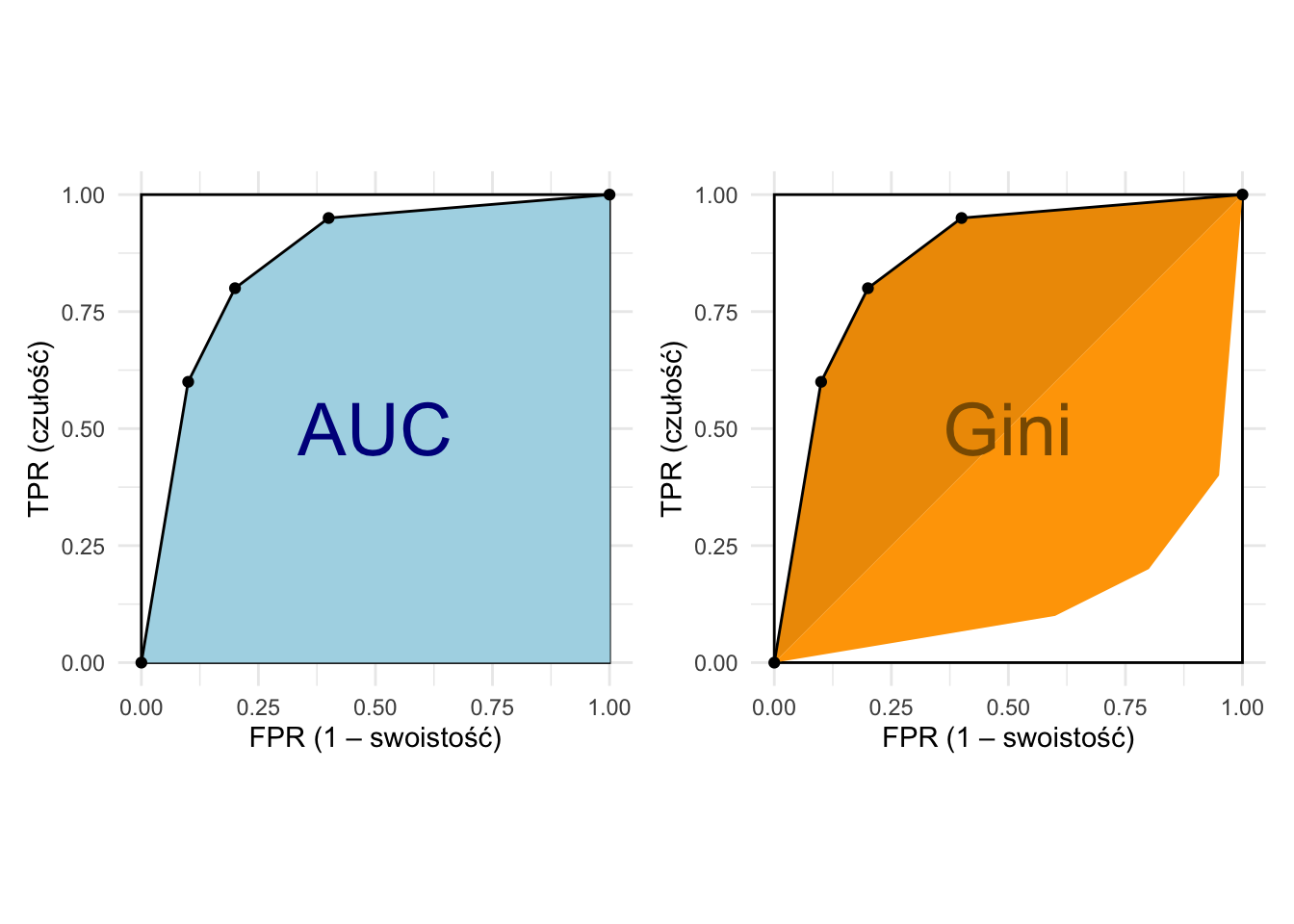
Rysunek 3.2: Interpretacja geometryczna: AUC (AUROC) to pole pod krzywą ROC, Gini to dwukrotność pola między przekątną y=x a krzywą ROC
Idealny model scoringowy osiąga AUC równe 1. Z kolei model losowy (niedziałający) generuje krzywą ROC przebiegającą w pobliżu przekątnej kwadratu, co skutkuje wartością AUC bliską 0,5.
AUC jest nazywane prawdopodobieństwem przewagi (ang. probability of superiority) albo potoczną miarą wielkości efektu (ang. common language effect size). Miara ta może być interpretowana jako prawdopodobieństwo, że model scoringowy losowej obserwacji pozytywnej przypisze wyższe prawdopodobieństwo przynależności do klasy pozytywnej niż losowej obserwacji negatywnej. Taka interpretacja AUC zakłada, że w przypadku gdy obie wylosowane obserwacje, pozytywna i negatywna, mają tę samą ocenę punktową, decyzję, która „wygrała”, podejmujemy na podstawie rzutu monetą.
W przypadku scoringu kredytowego można to zapisać w następujący sposób:
\[ \text{AUC} = \mathbb{P}(s_B < s_G) + \frac{1}{2}\mathbb{P}(s_B=s_G), \tag{3.5} \]
gdzie \(s_B\) to ocena punktowa losowo wybranej obserwacji pozytywnej (czyli kredytu „złego”, niespłacanego, ang. bad), zaś \(s_G\) to ocena punktowa losowo wybranej obserwacji negatywnej (jednostki „dobrej”, ang. good).
Miara AUC jest popularna w uczeniu maszynowym. W kontekście bankowych modeli scoringowych, zamiast miary AUC często w praktyce stosuje się współczynnik Giniego, który jest liniowym przekształceniem AUC:
\[ \text{Gini} = 2\text{AUC} - 1, \tag{3.6} \]
Współczynnik Giniego przyjmuje wartość 1, gdy model jest idealny, zaś 0 w przypadku modelu niedziałającego, co jest bardziej intuicyjne2. Współczynnik Giniego jest równoważny mierze D Somersa obliczonej dla zmiennej porządkowej lub ilościowej X (ocena punktowa) względem zmiennej zero-jedynkowej Y (etykieta klasy).
Współczynnik Giniego można również zinterpretować przez prawdopodobieństwa, podobnie do równania (3.5). Współczynnik Giniego to różnica prawdpodobieństwa, że ocena punktowa klienta złego będzie niższa niż ocena punktowa dobrego oraz prawdopodobieństwa, że będzie odwrotnie:
\[ \text{Gini} = \mathbb{P}(s_B < s_G) - \mathbb{P}(s_B > s_G), \tag{3.7} \]
Warto podkreślić, że mimo zbieżności nazw, scoringowy współczynnik Giniego nie jest tożsamy ze wskaźnikiem Giniego stosowanym do pomiaru nierówności dochodowych czy majątkowych. Obie miary łączy jedynie podobieństwo graficznej interpretacji (zob. rysunek 3.2), jednak dotyczą one wykresów, w których osie przedstawiają zupełnie różne wielkości.
AUC, a tym samym również współczynnik Giniego, można obliczyć z wykorzystaniem wzorów, które wprost nie odwołują się do krzywej ROC3. W pakietach statystycznych dostępne są funkcje obliczające AUC. Jako argumenty wejściowe przyjmują one najczęściej dwa wektory (dwie kolumny):
wektor zawierający ocenę punktową (lub inny wynik modelu predykcyjnego powiązany monotonicznie z prawdopodobieństwem zmiennej celu),
wektor zawierający zmienną celu, zwykle w formacie zero-jedynkowym.
# wektor ocen punktowych
score <- c(1, 1, 2, 3, 4, 4, 5, 5, 6, 7)
# wektor zmiennej celu (bad = 1, good = 0)
target <- c(1, 1, 0, 1, 0, 1, 0, 0, 1, 0)
# Obliczenie AUC (ze zmianą kierunku oceny punktowej)
bigstatsr::AUC(-score, target)## [1] 0.74Przy wyznaczaniu AUC należy zwrócić uwagę na kierunek modelu scoringowego względem zmiennej celu. W scoringu kredytowym wyższa punktacja oznacza niższe ryzyko (czyli mniejsze prawdopodobieństwo jedynki). To odwrotnie niż w większości innych zastosowań, gdzie wyższy wynik oznacza większe prawdopodobieństwo jedynki. Standardowe funkcje liczące AUC zakładają tę drugą konwencję, dlatego w przypadku scoringu kredytowego, aby obliczyć AUC, trzeba zwykle odwrócić punktację lub zmienną celu4. Tak właśnie zrobiono w powyższym przykładzie.
```
3.5 Zadania
Zadanie 3.1 W marcu 1884 roku sierżant J.P. Finley rozpoczął publikowanie prognoz dla 18 regionów USA. Prognozy były przygotowywane dwa razy dziennie. Po trzech miesiącach wyniki zaprezentował w następującej tabeli.
| Rzeczywistość: Tornado | Brak tornada | Razem | |
|---|---|---|---|
| Prognoza: Tornado | 28 | 72 | 100 |
| Prognoza: Brak tornada | 23 | 2680 | 2703 |
| Razem | 51 | 2752 | 2803 |
Ile wynosiła dokładność (accuracy) prognoz sierżanta Finleya? Ile wynosiłaby dokładność, gdyby za każdym razem przewidywał brak tornada?
Ile wynosiła czułość i swoistość prognoz sierżanta Finleya?
Uwaga! Tablica pomyłek może być prezentowana na dwa sposoby: z rzeczywistymi klasami w wierszach i przewidywanymi w kolumnach lub odwrotnie. Nie ma też jednej reguły, czy najpierw przedstawiona jest klasa pozytywna czy negatywna. Warto to sprawdzić przed analizą.↩︎
Współczynnik Giniego można potraktować jako miarę korelacji (związku statystycznego) między zmienną ilościową lub porządkową a zmienną zero-jedynkową↩︎
Takie wzory mogą być na przykład oparte na statystyce U w teście Manna-Whitneya.↩︎
AUC(-score, target)alboAUC(score, 1-target)↩︎