Capitolo 3 Indici e grafici

3.1 Visualizzazione dei dati

Gran parte dell’analisi (statistica) dei dati si basa sull’idea di fornire sintesi efficaci degli stessi così da estrarre al meglio le informazioni che essi contengono su un determinato collettivo.

Vi sono varie strategie per ottenere riassunti dei dati in ambito descrittivo/esplorativo. Nell’ambito dell’inferenza statistica il concetto di riassunto dei dati può essere impostato in modo più formale.

In estrema sintesi tuttavia gli strumenti che si utilizzano in ambito esplorativo sono di fatto due e sono complementari:

utilizzo di misure sintetiche di specifiche caratteristiche dei dati (esempi banali sono la media e la varianza come misure, rispettivamente, di centralità e dispersione dei dati);
utilizzo di sintesi grafiche e di tecniche di visualizzazione.

L’idea di fondo è che l’elaborazione dei dati grezzi (pensiamo alla matrice dei dati) sia necessaria così da comprimere e rendere comprensibile l’informazione in essi contenuta oltre a renderla più semplice da comunicare e conservare.

Uno dei principi fondamentali è che l’elaborazione dei dati e la loro sintesi (con indici o grafici) comporti inevitabilmente una perdita di informazione: è il prezzo da pagare per poter leggere i dati e per trarre da essi informazione utile. Ci si aspetta tuttavia che l’informazione che si perde sia non rilevante per interpretare il fenomeno e ottenere una visione di insieme delle caratteristiche salienti del collettivo che si sta esaminando.

3.1.1 Le tabelle di frequenza

La più semplice elaborazione è quella che conduce alle tabelle di frequenza: essa è un primo esempio di sintesi dei dati.

Per chiarire le idee, consideriamo il data frame del package “insuranceData” che contiene i dati relativi ai danni liquidati per sinistri dichiarati a un’assicurazione. Esso contiene sia variabili categoriali che quantitative continue (una descrizione dei dati ed è stata già introdotto nella prima parte del corso). Costruiamo la semplice tabella relativa alla variabile categoriale AutoBi$Attorney.

library(insuranceData)
data("AutoBi")
table(AutoBi$ATTORNEY)

## 
##   1   2 
## 685 655

Le informazioni sulla variabile riguardante il ricorso all’avvocato nei dati AutoBi sono in una colonna del data frame e l’obiettivo è sapere se in quel collettivo si tenda a ricorrere spesso all’avvocato. La tabella di frequenza riassume tali informazioni in modo efficace e ci permette di sapere che nell’insieme di dati si ricorre all’avvocato irca nella stessa misura con cui non si ricorre. Se si conservasse solo la tabella si perderebbe il dettaglio informativo sul singolo caso, sulla scelta o meno dell’avvocato che è contenuta nella specifica riga della matrice dei dati, tuttavia questa informazione è irrilevante per rispondere all’obiettivo conoscitivo. Il pezzo di informazione che ho perso è in questo caso trascurabile.

Si consideri, ad esempio, ora la variabile LOSS (sempre del data frame AutoBi). Anche per essa costruiamo una tabella di frequenza. Questa tabella contiene le frequenze assolute.

Tuttavia per fare questa semplice elaborazione e costruire la tabella della variabile quantitativa è necessario considerare le classi di valori e quindi trasformare la variabile in fattore: invece del singolo dato (che in questo caso sarà verosimilmente diverso per ogni unità) conservo solo la categoria ovvero la classe cui quel valore apparteneva.

AutoBi$LOSSclass<-cut(AutoBi$LOSS,breaks=c(0,0.5,2,4,8,1100)) 
table(AutoBi$LOSSclass) # tabella delle frequenze assolute
prop.table(table(AutoBi$LOSSclass)) # tabella delle frequenze relative

## 
##     (0,0.5]     (0.5,2]       (2,4]       (4,8] (8,1.1e+03] 
##         288         324         396         195         137 
## 
##     (0,0.5]     (0.5,2]       (2,4]       (4,8] (8,1.1e+03] 
##   0.2149254   0.2417910   0.2955224   0.1455224   0.1022388

La tabella fornisce una sintesi del fenomeno in esame: ad esempio ora si vede che coloro che hanno subito un danno sotto i 2000 dollari rappresentano circa il 45% dei casi.

La sintesi è molto più leggibile rispetto alla lista di 1340 valori riportati nella relativa colonna del data frame. Però nel fare la tabella si sono perse informazioni. Se si disponesse della sola tabella, non sarebbe possibile sapere se vi sono e quanti sono i casi che hanno un danno fra 1500 e 2000 dollari. Nel fare la sintesi si sono persi quindi alcuni dettagli e occorre chiedersi quale sia il livello di sintesi ottimale che bilanci la necessità di chiarezza e la perdita di informazione.

Il compromesso fra l’esigenza di sintesi e quella di mantenere il dettaglio informativo è un motivo ricorrente dell’analisi dei dati e in generale dell’elaborazione statistica.

Nella scelta di una opportuna sintesi numerica o di una tecnica grafica questo sarà quindi un tema sempre presente. In molti casi le visualizzazioni grafiche risultano più flessibili e maggiormente in grado di conservare buona parte dell’informazione originale.

3.1.2 Primi semplici grafici con `R`

Si introdurranno ora prime semplici rappresentazioni grafiche, immediatamente comprensibili, e alcune ben note, che ci consentiranno anche di iniziare a esplorare le enormi potenzialità grafiche di R.

Le tabelle di frequenza rappresentano una delle più elementari forme di elaborazione e sintesi dei dati. Ad esse si possono associare alcune rappresentazioni grafiche che quindi utilizzeranno direttamente i dati riassunti nell’oggetto generato dal comando table().

3.1.2.1 Il diagramma a torta

Si prenda in esame il data set Cars93 (già visto in precedenza)

library(MASS)
data("Cars93")

La variabile Type, il tipo di auto, è qualitativa per cui possiamo ottenere la tabella di frequenza

tabtipo<-table(Cars93$Type)

Possiamo associare a tale tabella il cosidetto “pie chart” o, in italiano, diagramma a torta con la funzione pie().

pie(tabtipo)

La fetta di torta corrispondente a ciascuna modalità ha un’area proporzionale alla frequenza della stessa.

Il diagramma a torta è tanto noto quanto, spesso, da sconsigliare. Se si legge la nota in fondo all’help su pie() in R si trova: “Pie charts are a very bad way of displaying information. The eye is good at judging linear measures and bad at judging relative areas. A bar chart or dot chart is a preferable way of displaying this type of data”.

3.1.2.2 Il diagramma a barre: `barplot()`

Un diagramma adatto a rappresentare variabili qualitative, o meglio le tabelle di frequenza ottenute con fattori qualitativi è costituito dal diagramma a barre (barplot o barchart in inglese).

Anche in questo caso la funzione barplot() si applica non al vettore di dati originale ma alla tabella di frequenze ricavata da esso. Vediamo un esempio con la variabile MARITAL del data frame AutoBi:

maritab<-table(AutoBi$MARITAL)
barplot(maritab)

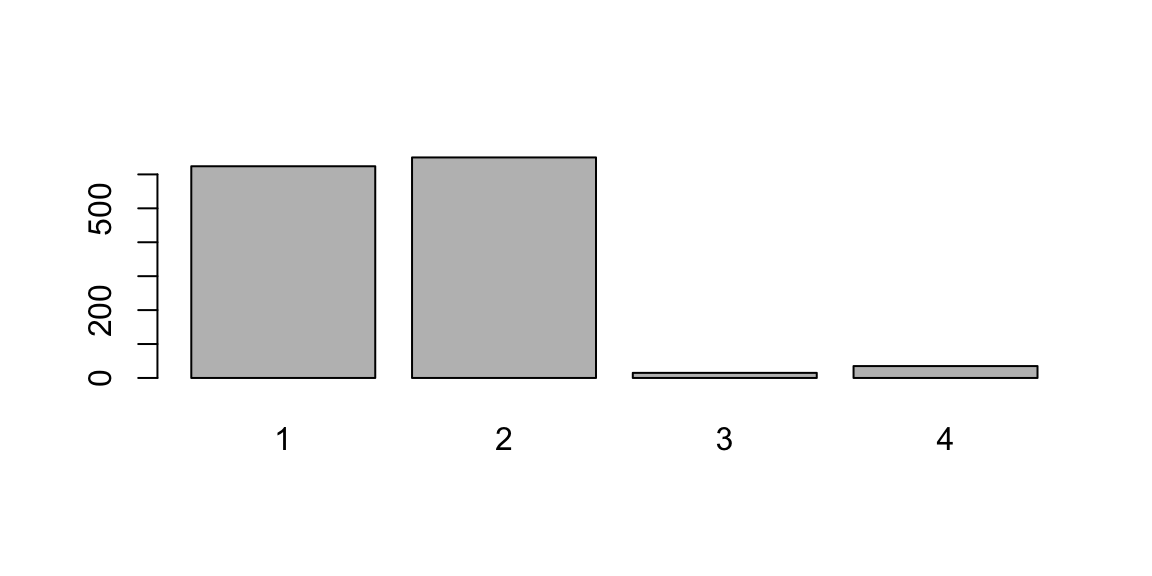
Stavolta le frequenze sono proporzionali alle altezze dei rettangoli ciascuno dei quali rappresenta una modalità. La funzione contiene alcuni parametri che consentono di personalizzare il grafico. ad esempio:

par(mfrow=c(1,2))
# questa funzione serve per fissare alcuni parametri della finestra grafica: 
# in questo caso divide la finestra grafica in due colonne e una riga. Per cui 
# affiancherà i due grafici successivi. Si noti che nel secondo grafico
# sono anche utilizzati alcuni parametri per mettere il titolo al grafico 
# (main="titolo" o per cambiare il colore col="2")
barplot(maritab)      
barplot(maritab, main="stato civile", names.arg=c("sposato", "single",
                                      "vedovo", "divorziato"), col=2)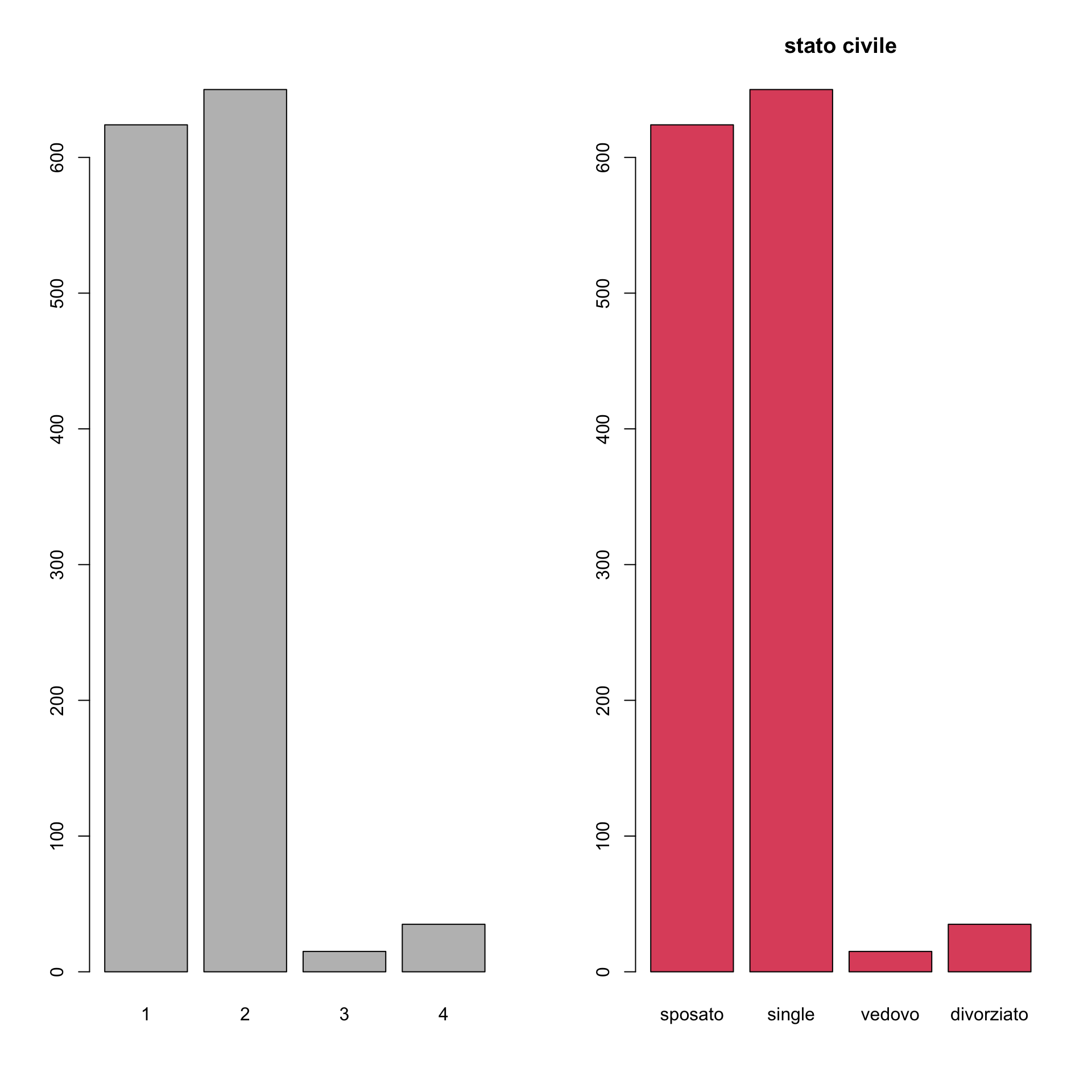

par(mfrow=c(1,1))  # così torniamo ad avere un solo grafico 
                  # per ciascuna finestra grafica
maritab1<-table(AutoBi$MARITAL)/
  length(AutoBi$MARITAL[!is.na(AutoBi$MARITAL)])
# In questo caso consideriamo le frequenze relative 
# si noti che abbimao diviso per il numero di casi escludendo gli NA
barplot(maritab1, main="stato civile con frequenze relative", 
        names.arg=c("sposato", "single", "vedovo", "divorziato"), col=3)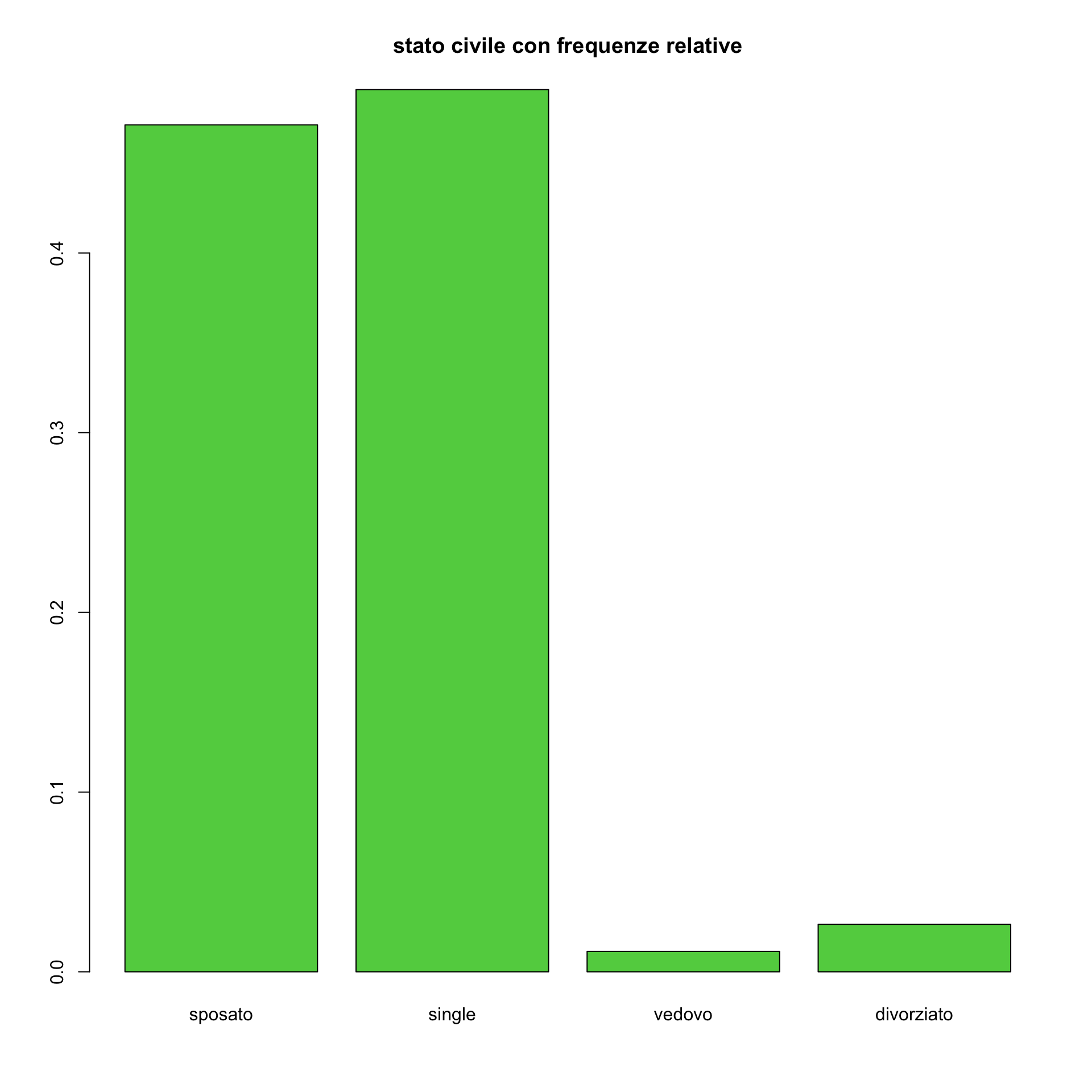

# diagramma a barre con le frequenze relative

Si vede bene che ogni rettangolo è separato, la sua larghezza e la posizione sull’asse orizzontale è arbitraria. Questo deve far riflettere sul fatto che tale grafico possa essere poco appropriato se la tabella di frequenze riguarda una variabile quantitativa trasformata in fattore con il metodo delle classi di valori.

Infatti in quest’ultimo caso i valori numerici postrebbero essere rappresentati più apportunamente sull’asse orizzontale. In particolare, ma non solo, se si tratta di una variabile quantitativa continua.

Il messaggio è quindi: no utilizzare il barplot per rappresentare una variabile quantitativa continua (in classi).

Talvolta esso si può tuttavia utilizzare con una variabile discreta con un numero di valori molto basso. ad esempio nel caso del numero di cilindri nel data set delle auto.

barplot(table(Cars93$Cylinders))

3.1.2.3 Il diagramma a barre sovrapposte

Un altro metodo per rappresentare una distribuzione di frequenza è quello di ricorrere al diagramma a barre “impilato”. Invece di avere una barra separata per ogni frequenza si rappresentano in un’unica barra le porzioni relative a ciascna modalità con le frequenze rappresentate dalla lunghezza di ciascuna porzione. Si suddividono le modalità con dei segmenti di un unico rettangolo la cui lunghezza è proporzionale alla frequenza (versione ‘stacked’). Occorre che i dati della tabella di frequenza siano trasformati in un vettore colonna (una matrice con tante righe quante le modalità e una solo colonna).

# esempio con stato civile 
par(mfrow=c(1,2))
freq<-matrix(prop.table(table(AutoBi$MARITAL)),
             nrow=length(table(AutoBi$MARITAL)), ncol=1)
barplot(freq, xlim=c(0,4), col=(2:5), )
# esempio con auto
nrig=length(table(Cars93$Type))
autof<-matrix(table(Cars93$Type), nrig, ncol=1)
colr=(2:(nrig+1))
barplot(autof, xlim=c(0,4), col=(2:(nrig+1)))
legend(x="bottomright", legend=levels(Cars93$Type), fill=colr)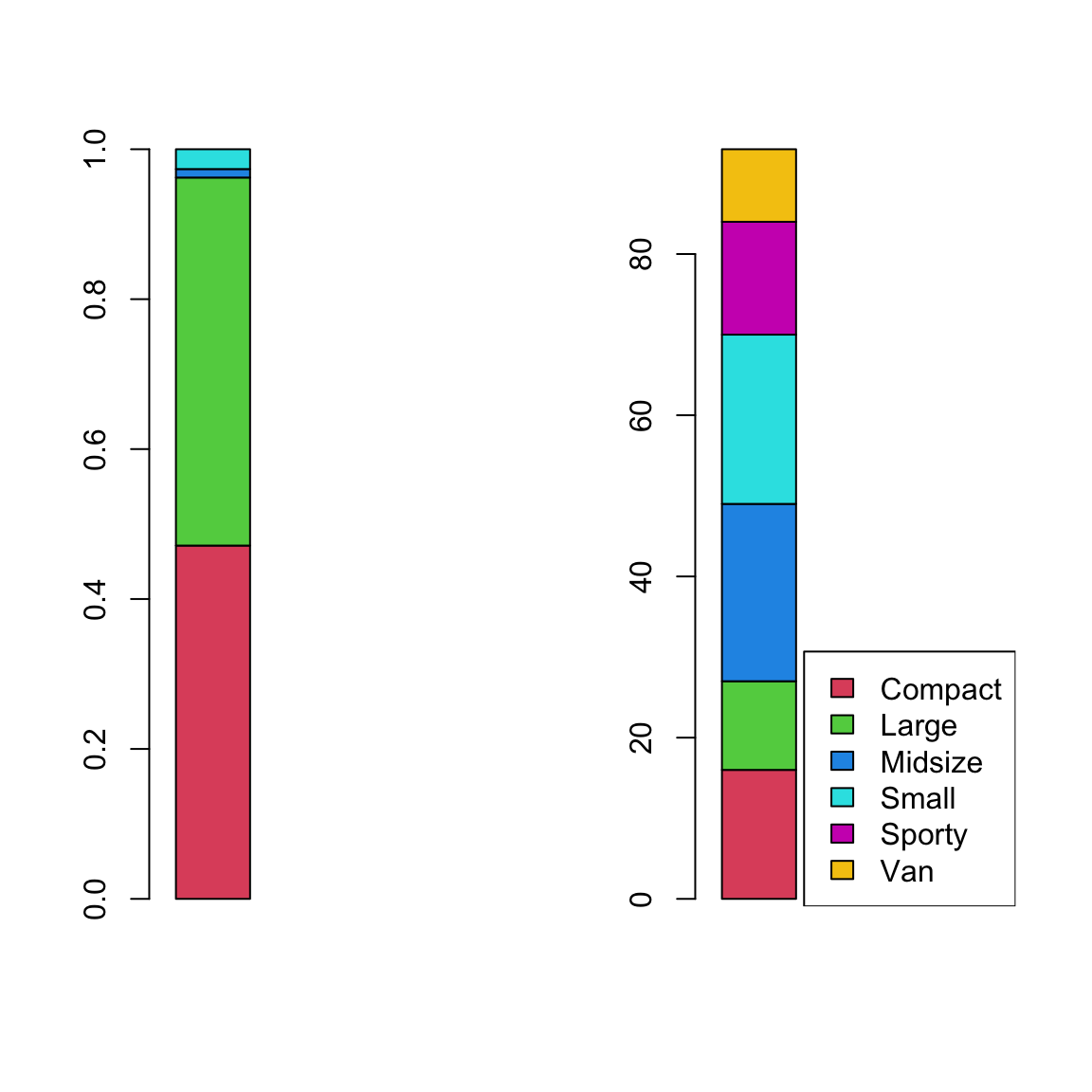

par(mfrow=c(1,1))

3.1.3 Rappresentare graficamente variabili quantitative: primi elementi

Nel caso dell’analisi di variabili quantitative abbiamo già osservato che occorre maggiore attenzione poichè l’eventuale riassunto grafico (o numerico) può comportare una più sensibile perdita di alcune informazioni. Occorre sempre chiedersi se la perdita di informazione è ben bilanciata dalla qualità informativa del riassunto stesso.

Nel seguito si introdurranno elementi per analizzare variabili quantitative mediante rappresentazioni grafiche e attraverso riassunti numerici. Vale la pena di segnalare che gli strumenti che verranno introdotti sono riferiti all’analisi di variabili quantitative continue. Tuttavia essi sono in genere del tutto adeguati anche nel caso di variabili discrete e specialmente nel caso di variabili discrete che assumono tanti valori distinti: ad esempio, se le unità statistiche fossero i comuni italiani e la variabile la popolazione degli stessi (si tratta evidentemente di una variabile discreta), ci si aspetta che la variabile assuma valori dell’ordine delle centinaia e che verosimilmente osserverei quasi esclusivamente valori distinti.

Se si tratta di variabili discrete (spesso di conteggio) che assumono solo valori bassi, quindi con pochi valori distinti (esempio sono la variabile numero di fratelli, o il numero di sinistri con l’auto che l’assicurato denuncia in un anno) l’uso dei semplici grafici visti per le variabili categoriali si rivela spesso del tutto adeguato. In tal caso anche i riassunti numerici che saranno illustrati, come ad esempio media, varianza, etc., sono comunque appropriati e possono essere utilizzati.

Si ricorda, invece, che i riassunti numerici e le rappresentazioni grafiche che si introdurranno, non devono essere utilizzate mai per variabili qualitative/fattori/categoriali. Tale errore spesso si fa se le variabili sono rappresentate invece che con la modalità con un valore numerico (ad esempio dopo una operazione di ricodifica). È per tale motivo che risulta sempre opportuno, nell’analisi con R, la trasformazione di tali variabili in fattori perchè il software sarà spesso in grado di decidere correttamente quale strumento va utilizzato.

3.1.3.1 Il diagramma ramo e foglie (stem and leaf)

Un semplice grafico che ha il vantaggio peraltro di non perdere informazione relativamente alla variabile quantitativa è il diagramma ramo e foglie. In R viene evocato con la funzione stem(). Ad esempio, si consideri la lunghezza in pollici delle auto:

Cars93$Length
stem(Cars93$Length)

##  [1] 177 195 180 193 186 189 200 216 198 206 204 182 184 193 198 178
## [17] 194 214 179 203 183 203 174 172 181 175 192 180 174 202 141 171
## [33] 177 180 179 176 192 212 151 164 175 173 185 168 172 166 184 200
## [49] 188 191 205 219 164 172 184 190 169 175 187 166 199 172 190 170
## [65] 181 190 188 188 190 194 201 173 177 181 196 195 177 184 176 146
## [81] 175 179 161 162 174 188 187 163 187 180 159 190 184
## 
##   The decimal point is 1 digit(s) to the right of the |
## 
##   14 | 16
##   15 | 19
##   16 | 123446689
##   17 | 0122223344455556677778999
##   18 | 000011123444445677788889
##   19 | 000001223344556889
##   20 | 001233456
##   21 | 2469

Come si vede il grafico è costituito da valori a destra di una linea verticale che corrispondono alla prime due cifre della variabile (il ramo). A sinistra della linea viene messa la terza cifra (ordinando dalla più bassa alla più alta). Tali cifre si impilano e la lunghezza della pila (la foglia) rappresenta direttamente la frequenza assoluta. La scelta di cosa usare come ramo è arbitraria e va fatta considerando i valori assunti dalla variabile.

Il grafico viene utilizzato per piccoli insiemi di dati (di solito non superiori al centinaio di casi). Se i casi sono più numerosi o se vi sono variabili molto disperse (per cui risulta difficile trovare efficacemente i valori da usare per il ramo) la rappresentazione risulta meno efficace e sarà necessario perdere qualche dettaglio: ad esempio se provo a usarla con AutoBi$LOSS

stem(AutoBi$LOSS)

## 
##   The decimal point is 2 digit(s) to the right of the |
## 
##    0 | 00000000000000000000000000000000000000000000000000000000000000000000+1251
##    1 | 015699
##    2 | 27
##    3 | 
##    4 | 
##    5 | 
##    6 | 
##    7 | 
##    8 | 
##    9 | 
##   10 | 7

è evidente che, in questo caso, lo stem & leaf non è una rappresentazione grafica efficace.

3.1.3.2 Il diagramma a punti

Il diagramma a punti, di fatto rappresenta su un grafico i singoli valori osservati. Per cui anche in questo caso non si perde alcun dettaglio. La funzione stripchart() del package graphics può essere usata a tale scopo.

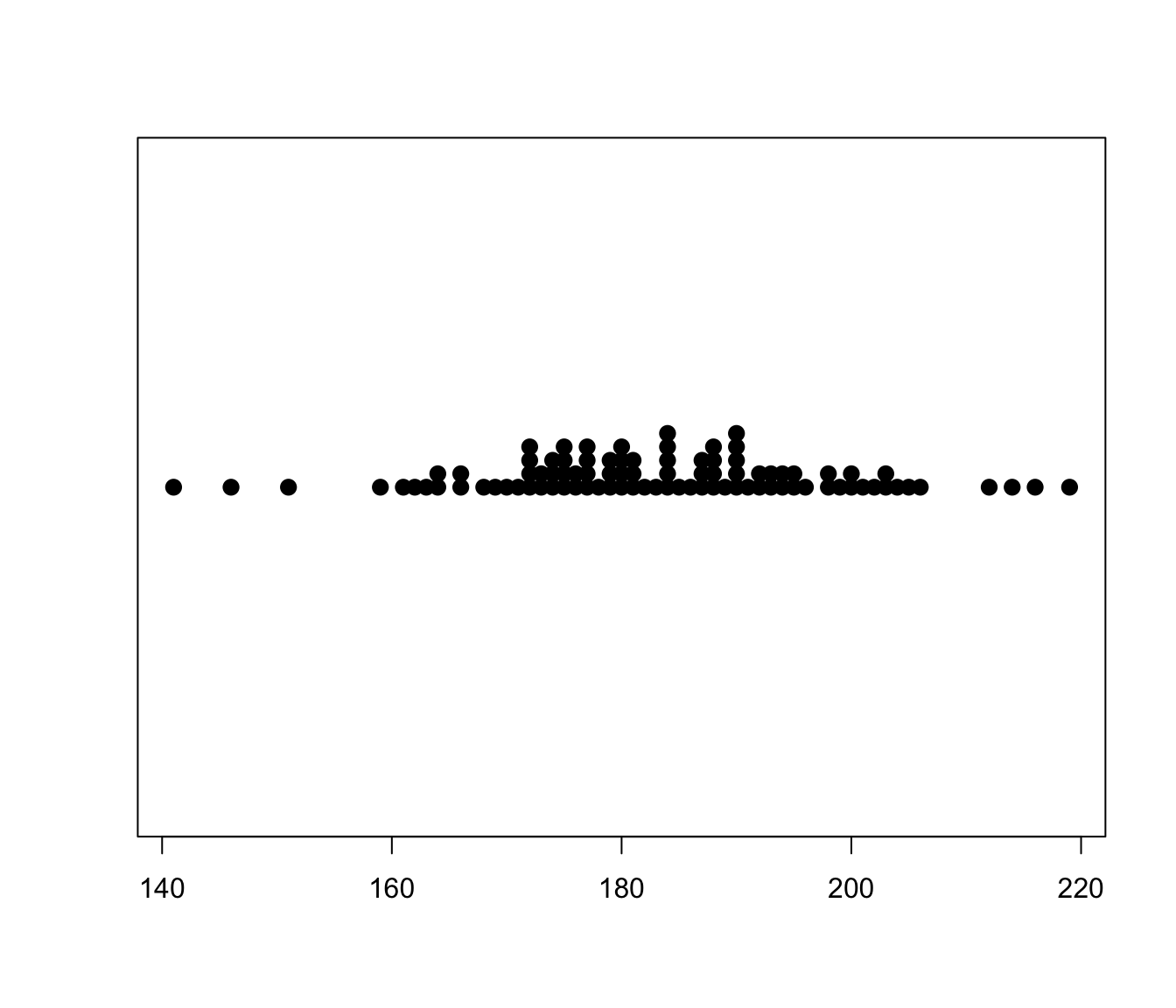
stripchart(Cars93$Length, pch=19, method="stack", cex=1.2, ylim=c(0,2))

# Si noti come nella funzione vengano fissati alcuni parametri. Si tratta di 
# parametri grafici che potranno essere utilizzati anche in altri casi Ad esempio 
# pch permette di scegliere quale simbolo utilizzare per rappresentare un punto 
# mentre cex permette di variare la grandezza del simbolo stesso

Il parametro method=stack consente di sovrapporre dati osservati che risultano spesso avere il medesimo valore. Il default è invece quello di mostrare il valore osservato senza dare conto della eventuale molteplicità.

Si considerino ad esempio i dati Ozone nel package mlbench e in particolare la variabile V4 che contiene il livello di concentrazione dell’ozono osservato (che appare misurato come una variabile che assume valori interi discreti) in California in tutti i giorni dell’anno

Anche in questo caso sono visibili i singoli valori.

3.1.3.3 Il diagramma a punti e la funzione `plot()`

Il diagramma a punti fornisce semplicemente la rappresentazione di ogni singolo punto osservato. Non vi è quindi alcuna sintesi dei dati. Tuttavia il suo utilizzo è certamente di interesse se si dispone di un numero limitato di casi da analizzare.

La funzione dotchart fa essenzialmente questo: rappresenta su un sistema di assi cartesiano i singoli punti.

dotchart(Cars93$Length)

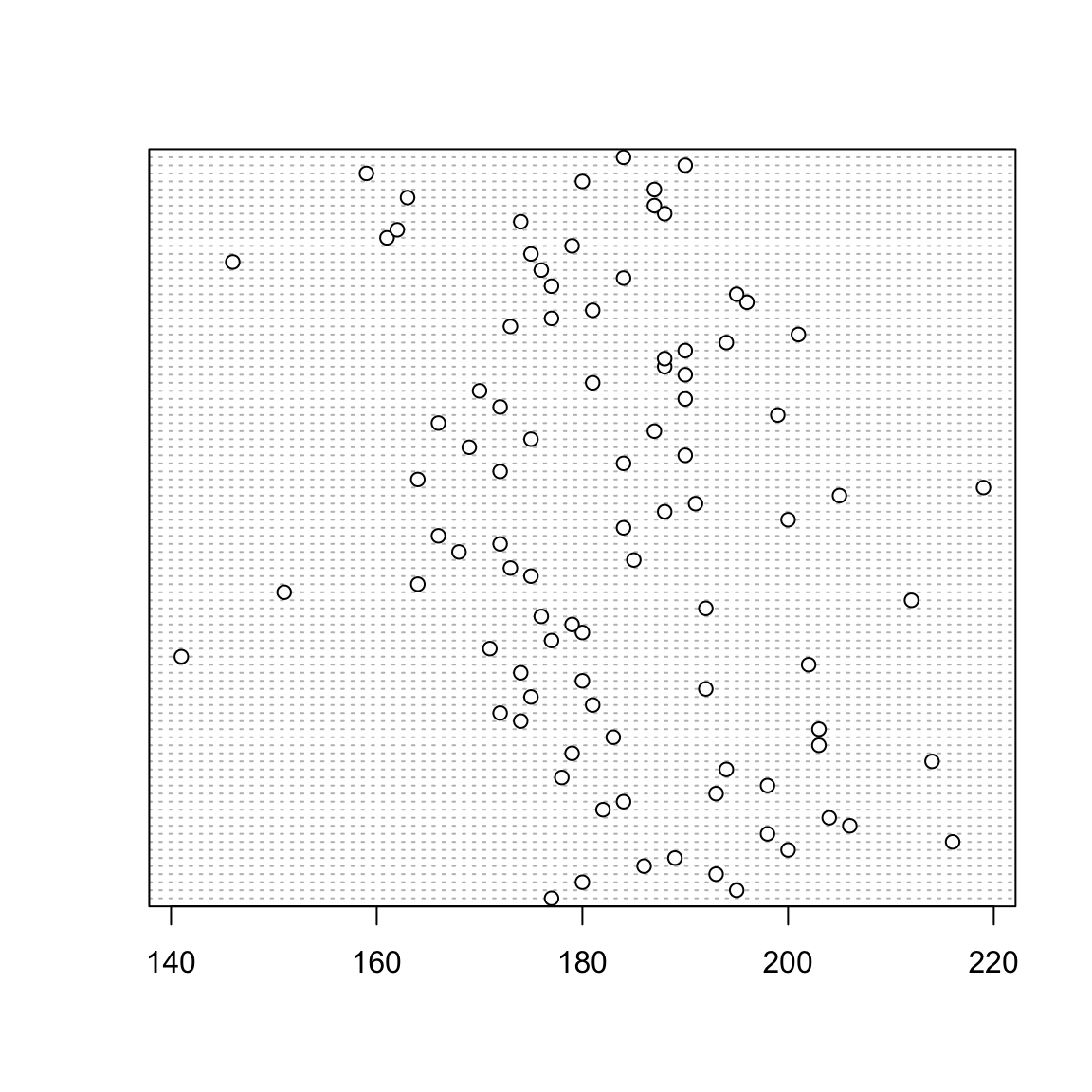
Le coordinate sull’asse verticale riflettono solo l’ordine con cui appaiono nella variabile le singole osservazioni.

E’ importante osservare che tale grafico è del tutto equivalente (nel senso che si sono solo invertiti gli assi) alla funzione plot(), che si introduce ora ma che verrà trattata con maggior dettaglio in seguito. Essa consente di riprodurre su un sistema di assi un’insieme di punti fornendo le loro coordinate. Di base quindi si dovrebbe fornire una coppia di vettori che rappresentano le coordinate dei singoli punti. Tale funzione è estremamente generale e consentirà di ottenere facilmente molte rappresentazioni grafiche di insiemi di dati bivariati (oltre che essere utilizzato per rappresentare graficamente, ad esempio, curve o funzioni di una variabile).

In effetti si può usare semplicemente

plot(Cars93$Length)

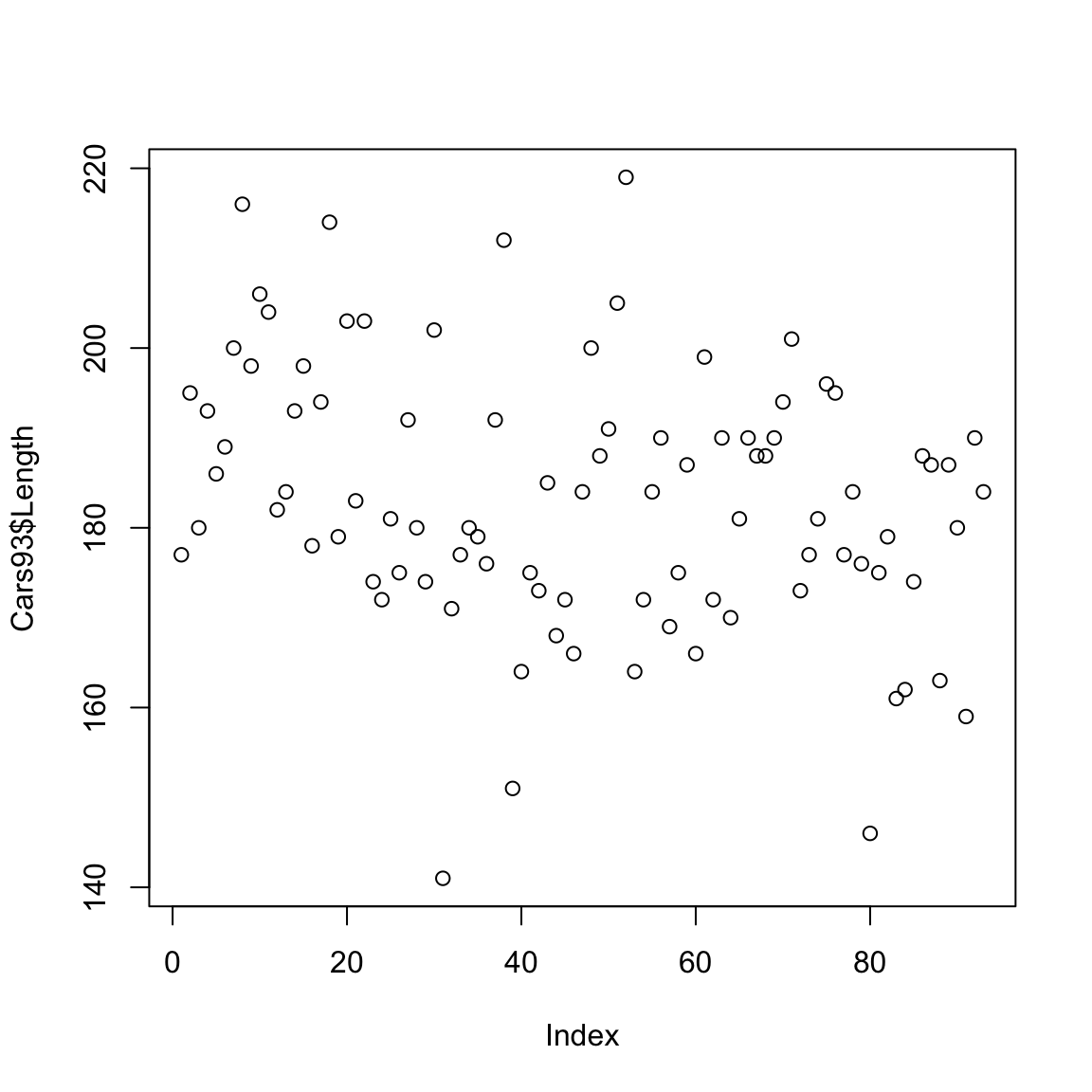
Il sistema si aspetta una coppia di variabili ma se se ne indica solo una, la coordinata sull’asse delle ascisse riporta semplicemente l’ordine con cui il valore appare nel vettore (che come si vede è chiamato Index nel grafico).

3.2 Riassunti numerici per variabili quantitative

Prima di procedere a illustrare altri metodi grafici per presentare un insieme di dati relativi a una variabile quantitativa converrà richiamare alcuni concetti di base che riguardano le misure di sintesi per riassumere le caratteristiche salienti di una variabile quantitiva (discreta o continua che sia).

Come si è già anticipato, quando si dispone dei dati per una variabile quantitativa è necessario sintetizzare e elaborare i dati così da fare emergere i fatti e le informazioni salienti. Spesso è necessario rinunciare a dettagli minuti che sono relativi a singole unità per tentare di dare una lettura di insieme del fenomeno con riferimento al collettivo da cui i dati sono tratti.

È una operazione essenziale per trasformare i dati grezzi in informazione.

L’attenzione va quindi concentrata su quali caratteristiche del collettivo sono di interesse e decidere se e come queste possono essere riassunte attraverso opportune sintesi numeriche.

I due aspetti dell’insieme di dati sui quali si concentrano le maggiori attenzioni sono:

la tendenza centrale: ovvero posso con un singolo valore riassumere l’ordine di grandezza del fenomeno di interesse?
la dispersione (o variabilità): cioè, un singolo valore può fornire un’idea di quanto i dati realtivi alla variabile siano diversi tra loro o, viceversa, quanto si somiglino?

Al fine di trattare tale argomento, e anche per sviluppi successivi, vale la pena di introdurre una notazione generale.

Rappresenteremo i valori assunti da una variabile quantitiva $X$ per un insieme di $n$ unità con la notazione $x_1, x_2, \dots, x_n$.

3.2.1 Indici di tendenza centrale (un solo valore al posto di tanti): le medie

Gli indici di tendenza centrale sono anche noti come medie. Si suole distingure far medie analitiche e medie di posizione.

3.2.1.1 Medie analitiche

La media aritmetica

La media aritmetica $M$ è di gran lunga la media analitica più nota e si calcola come

\[M=\sum_{i=1}^n\frac{x_i}{n}\] È già noto che in R esiste la funzione mean() che calcola la media aritmetica degli elementi di un vettore di dati quantitativi.

La media aritmetica ha alcune importanti proprietà:

assume un valore compreso fra $x_{(1)}=min(x_i)$ e $x_{(n)}=max(x_i)$
la somma delle differenze fra ciascun valore osservato e la media, in valore assoluto, è nulla: $\sum_{i=1}^n(x_i- M)=0$
ha la seguente proprietà di minimo $M=\underset{a \in R}{\arg \min}\sum_{i=1}^n(x_i-a)^2$

La terza proprietà si può leggere come segue:

se si decide che invece di ogni singolo dato $x_i$ si usa una sintesi che è $a$ potrei avere una perdita di informazione che decido di misurare con la differenza (scarto) dalla media al quadrato $(x_i-a)^2$: la perdita di informazione totale è quindi $\sum_{i=1}^n(x_i-a)^2$. La media $M$ è quel valore che rende minima tale perdita.

Inoltre dalla seconda proprietà consegue che $\sum_{i=1}^n x_i=nM$. Per cui si può dire che la media $M$ è quel valore che sostituito a ogni singolo dato lascia invariata la somma.

importante sottolineare che in molte situazioni ad ogni valore $x_i$ può essere associato un peso $p_i$ che denota l’importanza di tale valore. Un esempio riguarda i voti conseguiti negli esami: com’è noto essi hanno pesi diversi in quanto possono avre diversi CFU. Ma vale anche per il caso in cui alcuni valori vengono osservati più volte, accade ad esempio per le variabili quantitative discrete, e i dati quantitativi vengono riassunti in una tabella di frequenza: in tal caso la frequenza denota l’importanza di tale valore, il suo peso. In tal caso nel calcolare la media aritmetica occorre tenere conto dei pesi e si definisce la media aritmetica ponderata

\[M=\sum_{i=1}^n\frac{x_ip_i}{\sum_i^np_i}\]

Altre medie analitiche

Se si parte da questa ultima notazione, si potrebbe cercare un valore che analogamente alla media aritmetica, lascia invariata una certa funzione dei dati.

Ad esempio se invece della somma si considera il prodotto dei dati e si cerca la costante $M_g$ che lascia invariata questa funzione, cioè: $\prod_{i=1}^nx_i=M_g^n$ si ottiene la media geometrica. \[M_g=\left[\prod_{i=1}^nx_i\right]^{\frac{1}{n}}\]
Se il valore cercato lascia invariata la somma dei reciproci, si ottiene la media armonica \[M_{ar}=\frac{n}{\sum_{i=1}^n\frac{1}{x_i}}\]
Analogamente, si ottengono le medie di potenze $r$-esima (con $r$ intero) \[M_r=\left[\sum_{i=1}^n\frac{x_i^r}{n}\right]^{\frac{1}{r}}\] che hanno la proprietà di esser funziona monotona non decrescente di $r$. In virtù di ciò, e osservando che si potrebbe dimostrare che consoiderando il limite per $r$ che tende a 0 si ottiene la media geometrica, si ha quindi il seguente ordinamento $M_{ar} \leq M_g \leq M \leq M_2$ (ove l’uguaglianza vale se tutti i dati hanno lo stesso valore. Da questo segue anche che $M_2^2 \geq M^2$.
Si noti che la potenza $r$-esima della media potenziata di ordine $r$ definisce il momento empirico $r$-esimo.

3.2.1.2 I Quantili e le medie di posizione

Le medie (e gli indici) di posizione sono particolari valori che hanno una posizione definita rispetto la sequenza (ordinata) dei dati (si noti che non necessariamente essi appartengano alla sequenza stessa). A tal fine è importante introdurre il concetto di quantile empirico.

Fissata una proporzione $p$ (con $0\leq p\leq1$) si definisce $x_p$ quantile empirico di ordine $p$, con $p \in [0,1]$, quel valore $x \in \mathbb{R}$ tale che \[x_p: \frac{\#(x_i \leq x_p)} {n}= p\].

Si noti che dato un valore $p$:

non è detto che esista un unico valore $x_p$ che realizzi la condizione data;
potrebbe non esistere alcun valore che realizzi la condizione data, ma si potranno ritrovare valori di quantili $x_{p'}$ con $p'$ molto prossimo a $p$.

Se si considera la sequenza ordinata $x_{(1)}, x_{(2)} \dots, x_{(n-1)}, x_{(n)}$ per cui

$x_{(1)} \leq x_{(2)} \leq \dots, \leq x_{(n-1)} \leq x_{(n)}$

i valori definiscono i quantili di ordine $\frac{1}{n}, \frac{2}{n}, \dots , \frac{n-1}{n} , \frac{n}{n}$. Pertanto, il generico valore della sequenza ordinata $x_{(i)}$ rappresenta il quantile di ordine $p$, $x_p$ con $p=\frac{i}{n}$.

Si noti, inoltre, il rilievo che assume in questo contesto la definizione che specifica $x_p$ come il valore per cui sia $p$ la proporzione di valori minori o uguali a esso. Se disponiamo di un insieme di dati non particolarmente numeroso chiedere di contare i dati strettamente minori di $x_p$ o quelli minori o uguali può fare differenza. In tal caso infatti la sequenza ordinata fornirebbe i quantili $\frac{0}{n}, \frac{1}{n}, \dots , \frac{n-2}{n} , \frac{n-1}{n}$.

Per tale motivo a volte si preferisce adottare una diversa convenzione per cui i dati ordinati $x_{(1)} \leq x_{(2)} \leq \dots, \leq x_{(n-1)} \leq x_{(n)}$ rappresentano i quantili di ordine $\frac{0.5}{n}, \frac{1.5}{n}, \dots , \frac{n-1.5}{n} , \frac{n-0.5}{n}$. Cioè secondo tale convenzione $x_{(i)}$ rappresenta il quantile di ordine $x_{\frac{i-0.5}{n}}$ di ordine $p=\frac{i-0.5}{n}$.

Si noti che se $n$ è grande ci si attende che le differenze derivanti dalle diverse convenzioni saranno di scarso rilievo.

3.2.1.3 La mediana e i quartili

Come detto. alcuni particolari quantili hanno uno speciale rilievo. In particolare, i quantili $x_{0.25}, x_{0.5}, x_{0.75}$ sono detti quartili e denominati, ripettivamente, primo, secondo e terzo quartile.

Particolare rilievo ha poi il secondo quartile che è anche detto mediana.

La mediana $Me$ è quindi definita come quel valore per cui il 50% dei dati è inferiore (o uguale) a esso e una analoga percentuale è superiore.

Come si è osservato sopra, se cerchiamo il quantile $Me=x_{0.5}$ per un insieme di dati (con la condizione che siano il 50% quelli minori o uguali di $Me$) potremmo:

trovare infiniti valori che realizzino esattamente la condizione data (se ad esempio $n$ è pari)
non trovare alcun valore che realizzi la condizione data (ad esempio se $n$ è dispari).

La cosa si risolve convenzionalmente ponendo:

$Me = x_{\left(\frac{n+1}{2}\right)}$ se $n$ è dispari
$Me = \frac{x_{\left(\frac{n}{2}\right)}+x_{\left(\frac{n}{2}+1\right)}}{2}$ se $n$ è pari.

Si noti tuttavia che nel caso di $n$ pari, qualsiasi valore $x_{\left(\frac{n}{2}\right)} \leq x \leq x_{\left(\frac{n}{2}+1\right)}$ avrebbe la proprietà richiesta alla mediana.

La mediana è usata spesso in coppia con la media aritmetica per caratterizzare il valore centrale di una distribuzione. Si noti che la mediana ha una proprietà analoga a quella della media aritmetica. In particolare \[Me=\underset{a \in \mathbb{R}}{\arg \min}\sum_{i=1}^n|x_i-a|\] È cioè quel valore per cui è minima la somma dei valori assoluti delle distanze dei singoli dati da esso.

Come vedremo meglio, con esempi su vari insiemi di dati, la mediana è molto meno sensibile alla presenza di valori estremi (e anomali rispetto alla massa dei dati). In tal senso essa è più resistente. La media arimetica invece tende a essere molto influenzata da pochi valori estremi molto diversi dalla massa dei dati.

È quindi una buona regola guardare a entrambi i valori nel riassumere un insieme di dati.

Come per la media, esiste una funzione in R per calcolare la mediana usando la convenzione esposta.

median(Cars93$Length)
median(AutoBi$LOSS)

## [1] 183
## [1] 2.331

Anche il primo e il terzo quartile sono molto informativi sulla tendenza centrale della distribuzione: si noti infatti che, per definizione, il 50% dei valori centrali sono compresi fra di essi.

Per quanto riguarda la determinazione di tali due quartili, in particolare se $n$ non è molto elevato, vi sono difficoltà analoghe a quanto visto per la mediana. Per individuare i quantili occorre, come per la mediana, ricorrere a qualche convenzione. In R si usa l’interpolazione lineare fra i due quantili successivi osservati $x_{p_1}$ e $x_{p_2}$ tali che $p_1 \leq p \leq p_2$. (se si vuole approfondire si veda l’help della funzione quantile in cui vengono proposte anche altre strategie di approssimazione dei quantili)

Va infine ricordato che per caratterizzare la distribuzione dei dati oltre ai quartili (che dividono i dati ordinati in quattro porzioni ugualmente numerose) spesso si definiscono i decili (cioè i quantili $x_{0.1}, x_{0.2}, \dots, x_{0.9}$) o i percentili (cioè i quantili $x_{0.01}, x_{0.02}, \dots, x_{0.98}, x_{0.99}$).

In R la funzione quantile() consente di calcolare i quantili per diversi valori di $p$. La convenzione in questo caso è che la più piccola osservazione sia il quantile di ordine 0 e la più grande sia quello di ordine 1.

# se non si indica nulla vengono calcolati i quartili e i quantili di 
# ordine 0 e 1, cioè il massimo e il minimo
quantile(AutoBi$LOSS)

##         0%        25%        50%        75%       100% 
##    0.00500    0.64000    2.33100    3.99475 1067.69700

# si possono calcolare i decili per la variabile LOSS
quantile(AutoBi$LOSS, probs=seq(0,1,.1))

##        0%       10%       20%       30%       40%       50% 
##    0.0050    0.2380    0.4842    0.9970    1.6746    2.3310 
##       60%       70%       80%       90%      100% 
##    2.9700    3.6555    4.5148    8.0765 1067.6970

quantile(AutoBi$LOSS)

##         0%        25%        50%        75%       100% 
##    0.00500    0.64000    2.33100    3.99475 1067.69700

# Si verifichi infine che, banalmente, il quantile di ordine 0.5 è la mediana
median(AutoBi$LOSS)==quantile(AutoBi$LOSS, probs=0.5)

##  50% 
## TRUE

3.2.1.4 Riassunto dei 5 valori

Si è visto che i 3 quartili danno un riassunto interessante sulla distribuzione.

La mediana è un indice di tendenza centrale e i due quartili esterni danno un’idea di dove sia collocato il 50% centrale della distribuzione. Aggiungendo a questi il valore massimo e il valore minimo osservati nella sequenza di dati abbiamo un’idea di come i dati siano distribuiti sulle code.

I 5 valori (minimo, I quartile, mediana, III quartile, massimo) sono detti riassunto dei 5 valori (in inglese five numbers summary) e esiste una funzione fivenum()che li restituisce se applicata a un vettore di dati (numerici), inoltre gli stessi vengono restituiti anche nella funzione summary(), che, quando applicata a un vettore numerico, fornisce inoltre anche la media aritmetica. In entrambi i casi i valori mancanti vengono rimossi automaticamente. Ad esempio:

#  per la variabile LOSS  si ottengono il riassunto dei 5 valori e il summary
fivenum(AutoBi$LOSS)
summary(AutoBi$LOSS)

## [1]    0.0050    0.6400    2.3310    3.9955 1067.6970
##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
##    0.005    0.640    2.331    5.954    3.995 1067.697

3.2.1.5 Le medie sfrondate (trimmed)

Come si è detto, il principale indice di posizione, cioè la media aritmetica, rischia di essere molto influenzata dalla presenza di (pochi) valori difformi rispetto alla gran parte dei dati.

Un tema rilevante è se tali dati anomali (outliers) debbano essere esclusi dalle successive analisi o essere mantenuti. Come vedremo, su tale aspetto non esiste una regola generale perchè dipende dalla natura dei dati e in alcuni casi i fenomeni che osserviamo sono tali da poter ammettere che vi siano osservazioni estreme e quindi eliminare tali osservazioni potrebbe essere del tutto arbitrario e inappropriato.

Il tema che si pone è quindi quello comunque di trovare riassunti della tendenza centrale dei dati che non siano eccessivamente influenzati da tali dati anomali. A tal fine si possono calcolare delle medie dei dati disponibili sfrondando l’insieme dei dati dei valori troppo grandi e/o troppo piccoli.

Questo conduce a calcolare la media sfrondata fissando una proporzione $\alpha \in [0,1]$ di valori da escludere tra quelli estremi.

La funzione R che calcola la media di un vettore ha fra i parametri la possibilità di indicare se si vuole una media sfrondata. Ad esempio:

# calcoliamo la media sfrondata al 5% per la variabile LOSS
mean(AutoBi$LOSS, na.rm=TRUE, trim=0.05)
mean(AutoBi$LOSS, na.rm=TRUE)

## [1] 2.858701
## [1] 5.953461

3.2.2 Indici di dispersione (o variabilità)

L’altro importante aspetto di una distribuzione di dati è costituito dalla loro dispersione, ovvero si tratta di valutare e sintetizzare quanto i dati siano diversi l’uno dall’altro. Tale aspetto è anche detto variabilità.

Anche in questo caso si possono calcolare degli indici numerici che riassumano tale caratteristica e si possono proporre versioni più resistenti ai valori anomali.

3.2.2.1 La varianza, lo scarto quadratico medio, il coefficiente di variazione

La più nota misura di dispersione per un insieme di $n$ dati è la varianza. Essa è basata sulla quantità \[DEV=\sum_{i=1}^n(x_i-M)^2\] ovvero la somma degli scarti dalla media aritmetica che è detta devianza.

La varianza $V$ è la devianza media pertanto essa è definita come

\[ V=\frac{\mbox{devianza}}{n}=\sum_{i=1}^n\frac{(x_i-M)^2}{n}\] Quando tuttavia la varianza viene calcolata nell’ambito di un approccio inferenziale, ovvero essa non è semplicemente un indice di dispersione ma assume il ruolo di stimatore della varianza di una popolazione infinita da cui è tratto un campione casuale, si conviene usare la divisione per $n-1$. Poichè quest’ultimo contesto è piuttosto comune, non deve stupire che in R la varianza, calcolata con la funzione var(), è definita come $\frac{\mbox{devianza}}{n-1}=V\frac{n}{n-1}$.

È evidente che per $n$ elevato i valori che si ottengono nei due casi non si discostano molto e l’interpretazione in termini descrittivi non cambia nella sostanza. Tuttavia è bene essere consapevoli di quale versione si sta usando.

La devianza, e quindi la varianza, è tanto più grande quanto più i dati sono distanti da un valore centrale, che è la media aritmetica, che è candidato a rappresentarli tutti.

La varianza è calcolata in termini di distanze al quadrato e quindi non è espressa nella stessa unità di misura della variabile. Per tale motivo è frequente ricorrere alla radice quadrata dell’indice, che è detto scarto quadratico medio (SQM) o deviazione standard (in inglese standard deviation) \[ \mbox{SQM}= sd =\sqrt{V}\] che è espressa nella stessa unità di misura della variabile. In R la funzione che calcola lo scarto quadratico medio è sd() (basata sempre sulla varianza divisa per $n$-1).

Per definizione la varianza (e lo SQM) assumono solo valori positivi e sono pari a 0 solo nel caso che tutti i valori sono uguali tra loro (variabilità nulla).

L’interpretazione dell’indice non è sempre agevole non essendo definito un limite superiore. È spesso interessante utilizzarla per comparare, ad esempio, la variabilità in due insiemi di dati che hanno medie non troppo diverse tra loro.

Si riporta un esempio in cui con R si calcola la varianza in due insiemi di dati.

# si calcola la varianza  e la deviazione standard per la variabile LOSS 
# per i maschi e per le femmine
"Maschi"
var(AutoBi$LOSS[AutoBi$CLMSEX==1], na.rm=TRUE) 
sd(AutoBi$LOSS[AutoBi$CLMSEX==1], na.rm=TRUE)
"Femmine"
var(AutoBi$LOSS[AutoBi$CLMSEX==2], na.rm=TRUE)
sd(AutoBi$LOSS[AutoBi$CLMSEX==2], na.rm=TRUE)
##

## [1] "Maschi"
## [1] 301.0511
## [1] 17.35082
## [1] "Femmine"
## [1] 1745.729
## [1] 41.78192

Le medie nei due gruppi sono simili

# si ottiene la media per la variabile LOSS per i maschi e per le femmine
mean(AutoBi$LOSS[AutoBi$CLMSEX==1], na.rm=TRUE)
mean(AutoBi$LOSS[AutoBi$CLMSEX==2], na.rm=TRUE)
##

## [1] 5.652647
## [1] 6.213765

In questo caso, il confronto darebbe un’indicazione che vi è più variabilità nel caso delle femmine. Tuttavia è facile notare che tale maggiore variabilità è fortemente condizionata dalla presenza di valori anomali. A tal fine si consideri il summary dei due insiemi:

# varianza per la variabile LOSS per i maschi e per le femmine
summary(AutoBi$LOSS[AutoBi$CLMSEX==1])
summary(AutoBi$LOSS[AutoBi$CLMSEX==2])
##

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
##   0.030   0.628   2.372   5.653   3.901 222.405      12 
##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
##    0.0050    0.6905    2.2270    6.2138    4.0252 1067.6970 
##      NA's 
##        12

Si vede chiaramente come nel caso delle femmine si ottiene un valore estremamente elevato. Esso ha impatto sulla media (non sulla mediana) e di conseguenza anche sulla varianza. La varianza è quindi, come la media, un indice poco “resistente”.

3.2.2.2 Altre misure di variabilità: coefficiente di variazione, scarto interquartile, MAD

Come per la tendenza centrale anche per la variabilità esistono altre misure che hanno caratteristiche che li rendono in alcuni casi preferibili alla varianza o quanto meno è spesso consigliabile in una fase esplorativa affiancarli ad essa.

lo scarto interquartile: SI: è semplicemente definito come la differenza fra il III quartile e il I quartile, ovvero $SI=x_{0.75}-x_{0.25}$. Ovviamente risente meno dei valori estremi, ma tiene conto solo della dispersione nella parte centrale della distribuzione. Ovviamente è anche calcolabile direttamente dai dati che fornisce summary
il MAD: Scarto assoluto mediano dalla mediana. esso è definito come \[MAD=\mbox{Mediana}(|x_i-Me|)\] È un indice resistente, cioè non risente di eventuali valori anomali. Si calcola con la funzione mad().
il coefficiente di variazione: spesso il confronto fra la variabilità in due collettivi ha senso se nei due collettivi la variabile presenta valori che hanno circa lo stesso ordine di grandezza (i due gruppi cioè hanno media non eccessivamente diversa). Per ovviare a questo problema si introduce il coefficiente di variazione che è quindi un indice di variabilità relativo. Esso è semplicemente definito come il rapporto fra scarto quadratico medio e media aritmetica.

Vediamo ancora l’esempio precedente con i dati di LOSS separatamente per maschi e femmine.

# si ottiene la varianza e il MAD per la variabile LOSS sia per i maschi e 
# per le femmine
"varianza"
var(AutoBi$LOSS[AutoBi$CLMSEX==1], na.rm=TRUE)
var(AutoBi$LOSS[AutoBi$CLMSEX==2], na.rm=TRUE)
"MAD"
mad(AutoBi$LOSS[AutoBi$CLMSEX==1], constant=1, na.rm=TRUE)
mad(AutoBi$LOSS[AutoBi$CLMSEX==2], constant=1, na.rm=TRUE)
##

## [1] "varianza"
## [1] 301.0511
## [1] 1745.729
## [1] "MAD"
## [1] 1.6635
## [1] 1.6755

Si noti come la variabilità misurata dal MAD è molto simile nei due gruppi a testimonianza dell’impatto che l’unico valore estremo nel gruppo delle femmine aveva sul calcolo della varianza.

3.2.3 Simmetria e curtosi

Sintetizzare solo la tendenza centrale o la dispersione di una variabile quantitativa lascia in ombra molte altre caratteristiche della distribuzione dei dati. È pertanto buona regola guardare a altre specificità della distribuzione dei valori e eventualmente cercare dei valori che li sintetizzino.

Una rilevante caratteristica di un insieme di dati è legata alla tendenza degli stessi a distribuirsi in modo molto diverso nella parte sinistra della distribuzione (i valori bassi quindi) rispetto alla parte destra.

Se si fa riferimento a un indice di tendenza centrale, ad esempio la mediana, potrebbe accadere che i dati a destra siano molto più dispersi rispetto a quelli a sinistra ovvero la distribuzione presenta una coda a destra più lunga. Si dirà che la distribuzione ha una asimmetria positiva. Viceversa, se vi è una coda a sinistra più lunga si parla di asimmetria negativa.

Se accade questo i dati evidenziano una asimmetria (skewness in inglese) nella distribuzione della variabile. Il concetto complementare è quindi quello di simmetria che riguarda la situazione in cui i dati a destra e a sinistra del centro della distribuzione esibiscono un comportamento analogo.

È facile apprezzare la simmetria (o l’asimmetria) guardando ad alcuni percentili della distribuzione. Vediamo due esempi in cui consideriamo i decili di due variabili nei dati di AutoBI:

# si otengono i decili per le variabile LOSS e CLMAGE 
"LOSS"
quantile(AutoBi$LOSS, probs = seq(0,1,0.1), na.rm=T, digits=2)

"CLMAGE"
quantile(AutoBi$CLMAGE, probs = seq(0,1,0.1), na.rm=T)

## [1] "LOSS"
##        0%       10%       20%       30%       40%       50% 
##    0.0050    0.2380    0.4842    0.9970    1.6746    2.3310 
##       60%       70%       80%       90%      100% 
##    2.9700    3.6555    4.5148    8.0765 1067.6970 
## [1] "CLMAGE"
##   0%  10%  20%  30%  40%  50%  60%  70%  80%  90% 100% 
##    0   13   18   21   26   31   36   41   47   55   95

Confrontando i quantili a destra e a sinistra della mediana è evidente che la distribuzione della variabile età è meno asimmetrica della variabile LOSS.

Si tratta quindi di proporre degli indici sintetici che riassumano tale caratteristica (ovvero l’asimmetria).

3.2.3.1 Indici di simmetria basati su particolari quantili

Come si è visto un modo per valutare la simmetria è quello di guardare la posizione di alcuni quantili rispetto alla mediana. Avendo già discusso del rilievo che si dà ai tre quartili, un indice può esser costruito guardando alla posizione del secondo quartile $Q2=x_{.5}$, ovvero la mediana, rispetto agli altri quartili $Q1=x_{0.25}$ e $Q3=x_{0.75}$.

in assenza di asimmetria sarà $(Q3-Q2)=(Q2-Q1)$
se vi è asimmetria positiva (coda a destra lunga) $(Q3-Q2)>(Q2-Q1)$
se vi è asimmetria negativa (coda a destra lunga) $(Q3-Q2)>(Q2-Q1)$

Allora un indice (di Galton) basato sui quartili è il seguente: \[G=\frac{Q3+Q1-2Q2}{Q3-Q1}\] La stessa idea potrebbe applicarsi a quantili più estremi, ad esempio, il primo e il nono decile $x_{0.1}$ e $x_{0.9}$ confrontati con la mediana.

\[K=\frac{x_{0.9}+x_{0.1}-2x_{0.5}}{x_{0.9}-x_{0.1}}\]

3.2.3.2 Indici basati sul confronto fra media e mediana

Abbiamo già notato che il diverso comportamento di media e mediana è legato alle quantità che minimizzano e alla tendenza della media a essere influenzata da valori sulla coda della distribuzione. Quindi:

se la media è circa uguale alla mediana è un sintomo di assenza di asimmetria
se la media è superiore (inferiore) alla mediana è un sintomo di asimmetria positiva (negativa) in quanto avrò prevalenza di valori (alcuni molto distanti dalla media)sulla coda destra (sinistra)

Pertanto si può costruire un indice (coefficiente di asimmetria) come segue

\[\frac{3(M-Me)}{sd}\]

3.2.3.3 L’indice di asimmetria

L’altra possibilità è quella di costruire un indice basato sugli scarti dalla media elevati al cubo $(x_i-M)^3$. Ovviamente è rilevante in questo caso se uno scarto è positivo o negativo.

L’indice di asimmetria è definito come:

\[\gamma=\frac{\sum_{i=1}^n\frac{(x_i-M)^3}{n}}{sd^3}\]

Tale indice è nullo per una distribuzione simmetrica (a ogni valore superiore alla media ne corrsponderebbe un altro equidistante e inferiroe alla media) mentre assume valori positivi nel caso di asimmetria positiva (coda destra lunga) e negativi nel caso di asimmetria negativa (coda sinistra lunga).

In R esso può essere calcolato con la funzione skewness() che si trova nel pacchetto moments

library(moments)
# si ottengono varie misure di asimmetria per le variabili LOSS e CLMAGE
"LOSS"
"Indice di Galton"
Qloss<-fivenum(AutoBi$LOSS, na.rm=T)
g<-(Qloss[4]+Qloss[2]-2*Qloss[3])/(Qloss[4]-Qloss[2])
"Indice di asimmetria"
skewness(AutoBi$LOSS)
"CLMAGE"

## [1] "LOSS"
## [1] "Indice di Galton"
## [1] "Indice di asimmetria"
## [1] 25.68795
## [1] "CLMAGE"

3.2.3.4 Indice di curtosi

La curtosi è un’ulteriore caratteristica della distribuzione di una variabile quantitativa. Essa misura la tendenza, in distribuzioni simmetriche, di mostrare code corte che scendono velocemente allontanandosi dal centro della distribuzione oppure code più ‘pesanti’ Per cui non è difficile osservare valori distanti dal centro anche allontanandosi da esso.

Il punto di riferimento è il modello della gaussiana e in genere si valuta la curtosi proprio andando a comparare il comportamento delle code con quello della gaussiana.

L’indice di curtosi $\delta$ è definito come segue \[ \delta = \frac{\sum_{i=1}^n\frac{(x_i-M)^4}{n}}{sd^4}\]

Anch’esso è disponibile nel pacchetto sopracitato (moments) è sempre maggiore di 0 ed è pari a 3 se la curtosi è pari a quella della gaussiana. Se è minore di 3 allora la distribuzione ha code piu corte (rispetto alla gaussiana, leptocurtosi) nel caso contrario più lunghe (platicurtosi).

# si calcola l'indice di curtosi per la variabile CLMAGE
"CLMAGE"

kurtosis(AutoBi$CLMAGE, na.rm=TRUE)

# si osservi che la curtosi non è molto diversa da quella della gaussiana.

## [1] "CLMAGE"
## [1] 3.042604

3.2.4 Altri grafici per variabili quantitative

3.2.4.1 Il diagramma a scatola con baffi (boxplot)

Come si è visto il riassunto dei 5 numeri fornisce i 3 quartili che danno idea di diversi aspetti della distribuzione: tendenza centrale (la mediana), dispersione (scarto interquartile), simmetria (indice di Galton). Inoltre il minimo e il massimo danno indicazione di cosa accade sulla coda destra e sinistra.

Un’idea molto semplice ed efficace per riassumere graficamente le caratteristiche essenziali di una variabili quantitativa è quella che conduce al cosiddetto diagramma a scatola con baffi (box and whiskers plot). Conviene illustrarlo con un esempio utilizzando la funzione di R che permette di ottenerlo cioè boxplot().

fivenum(neo$Peso)

## [1] 2420.0 2734.5 3067.5 3311.5 3530.0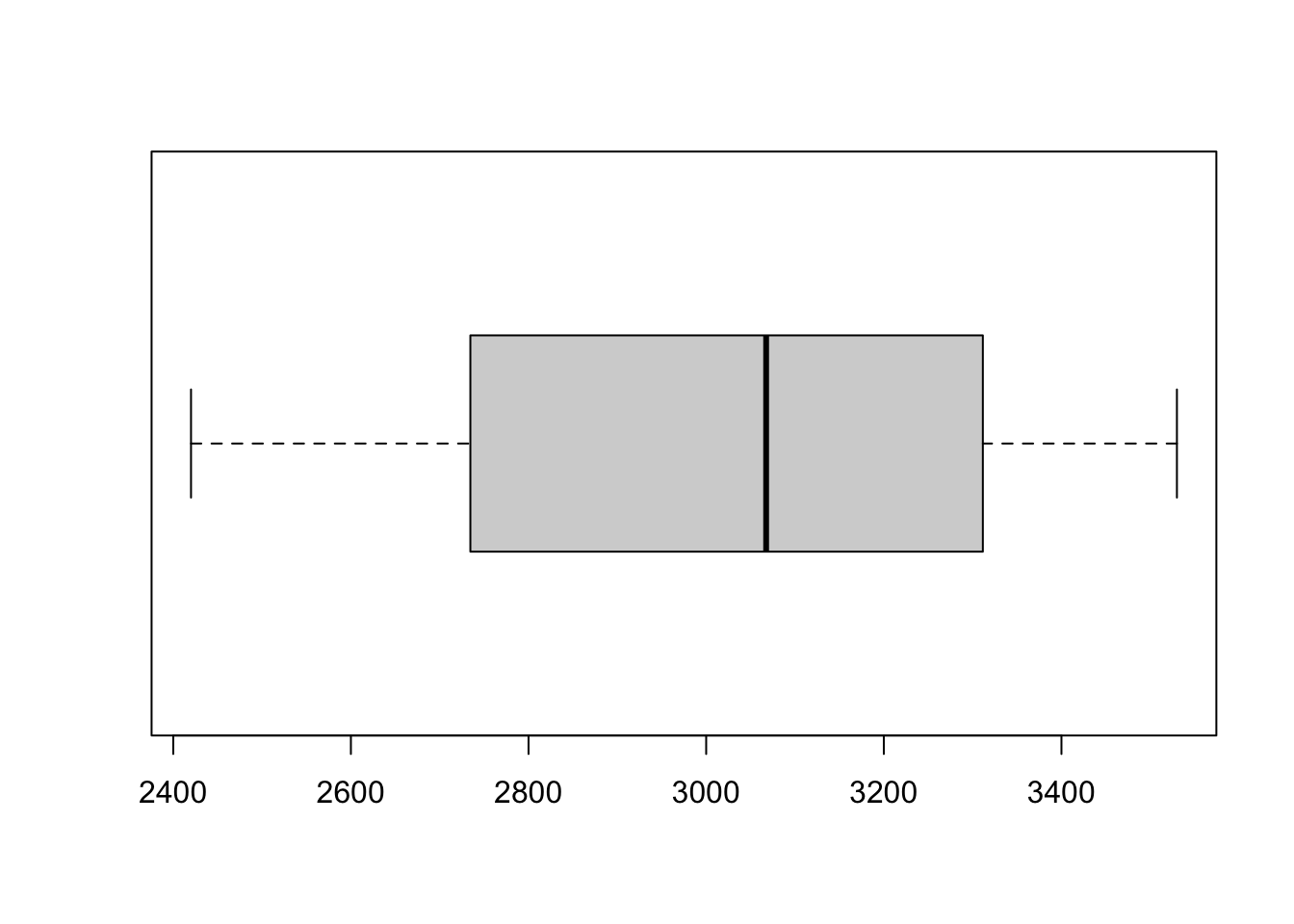

boxplot(neo$Peso, horizontal=TRUE)

# Si noti il parametro horizontal che ci consente di mettere la 
# scatola verticalmente o orizzontalmente

Come si vede si sono usati i dati forniti dal riassunto dei 5 numeri per disegnare la scatola. La scatola è posizionata con riferimento a un asse lungo cui sono i valori della variabile così che i bordi corrispondano al I e al III quartile (Q1 e Q3) mentre al suo centro la linea è in corrispondenza della mediana (Q2):

la larghezza della scatola ci dà quindi un’indicazione della dispersione;
la sua posizione ci da una indicazione di dove si trova il 50% dei valori centrali della variabile e assieme alla linea in corrispondenza della mediana ci dà indicazione dei valori centrali;
la posizione della mediana nella scatola ci informa sulla simmetria;
i baffi ci danno indicazione del comportamento sulle code.

Se tuttavia proviamo lo stesso grafico con una diversa variabile

fivenum(Cars93$Length)

## [1] 141 174 183 192 219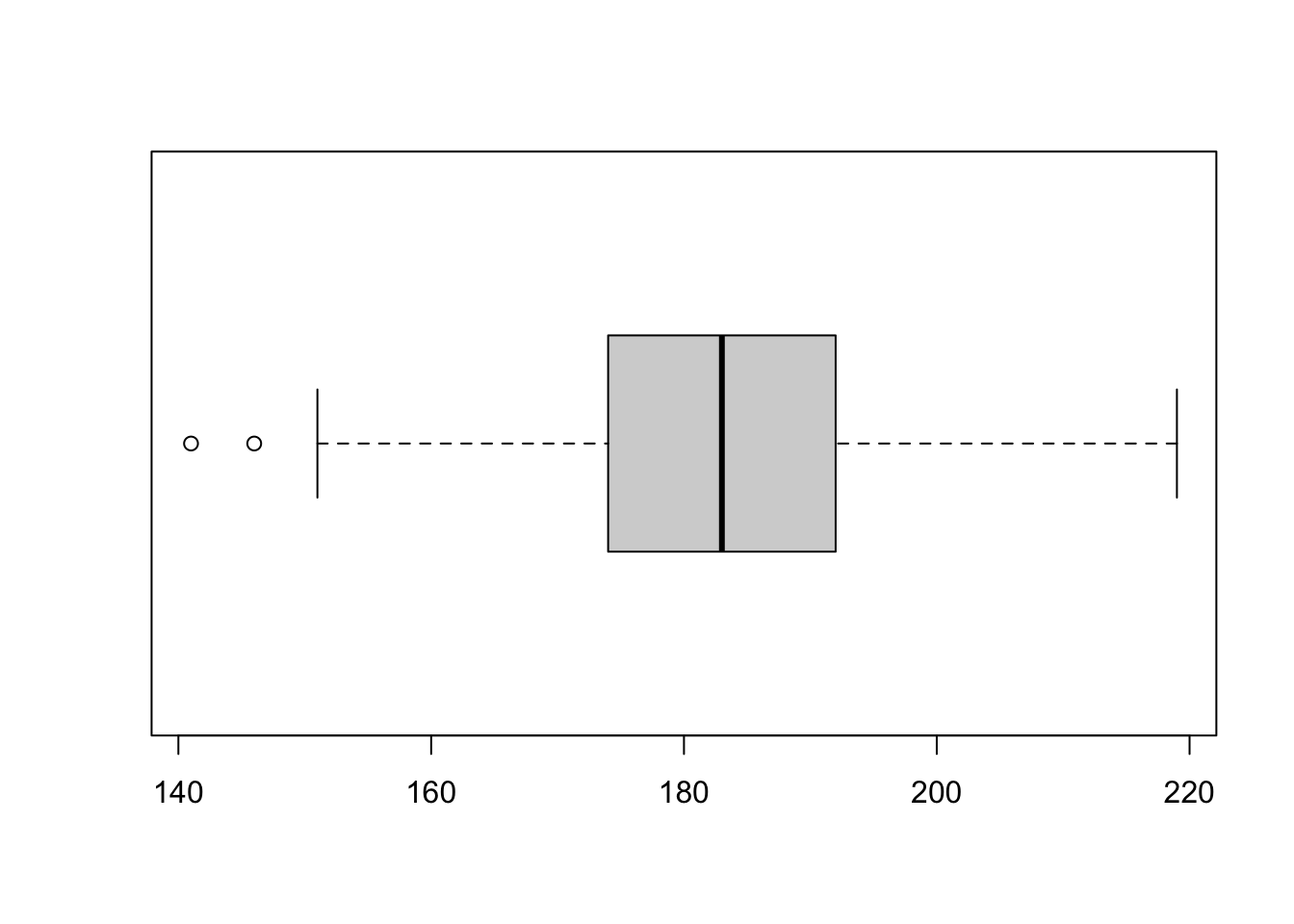

boxplot(Cars93$Length, horizontal=TRUE)

In questo caso il baffo sinistro non si estende fino al minimo. Inoltre vediamo sul grafico due punti rappresentati separatamente.

Questo perchè in realtà nel diagramma a scatola si evidenziano quei punti che sono ritenuti distanti dal resto dei dati (a destra o a sinistra). Tali valori sono detti outliers e vengono rappresentati isolatamente sul grafico.

La definizione di outlier nel diagramma a scatola si deriva dalla seguente regola:

sono oulier (valori anomali) quei valori che sono più distanti dai bordi della scatola (cioè dai quartili) più di una volta e mezza la differenza interquartile $SI=Q3-Q1$. Pertanto tutti i punti che sono superiori a $Q3+1.5SI$ o inferiori a $Q1-1.5SI$ verranno annotati separatamente sul grafico;
se essi esistono (a destra o a sinistra) di conseguenza il baffo non va esteso fino al massimo o al minimo valore osservato, va invece esteso:
- a destra, fino al più grande valore che non sia segnalato come outlier (cioè il massimo valore osservato che risulti inferiore a $Q3+1.5SI$);
- a sinistra, fino al più piccolo valore che non sia segnalato come outlier (cioè il minimo valore osservato che risulti superiore a $Q1-1.5SI$).

Il diagramma a scatola è una rappresentazione grafica usata molto frequentemente anche perchè è adeguata anche nel caso di un insieme molto limitato di casi ($n$=20 o 30).

Attenzione però che nel caso i valori siano pochi la regola con cui si determinano i quartili (che ha margini di arbitrarietà come abbiamo già discusso) può cambiare l’apparenza del grafico.

Anche nel caso del diagramma a scatola la presenza di code molto lunghe e/o dati molto estremi esso potrebbe risultare inefficace. Vediamo cosa accade ad esempio con la variabile $AutoBi$LOSS$ che abbiamo visto esser caratterizzata da una coda a destra lunghissima (forte asimmetria positiva) asimmetrica.

par(mfrow=c(1,2))
boxplot(AutoBi$LOSS)

# i valori elevatissimi presenti nella variabile vengono rappresentati
# separatamente, ma questo fa sì che la scatola diventi difficile da
# apprezzare sul medesimo grafico.

# Proviamo a usare la trasformata logaritmica
boxplot(log(AutoBi$LOSS))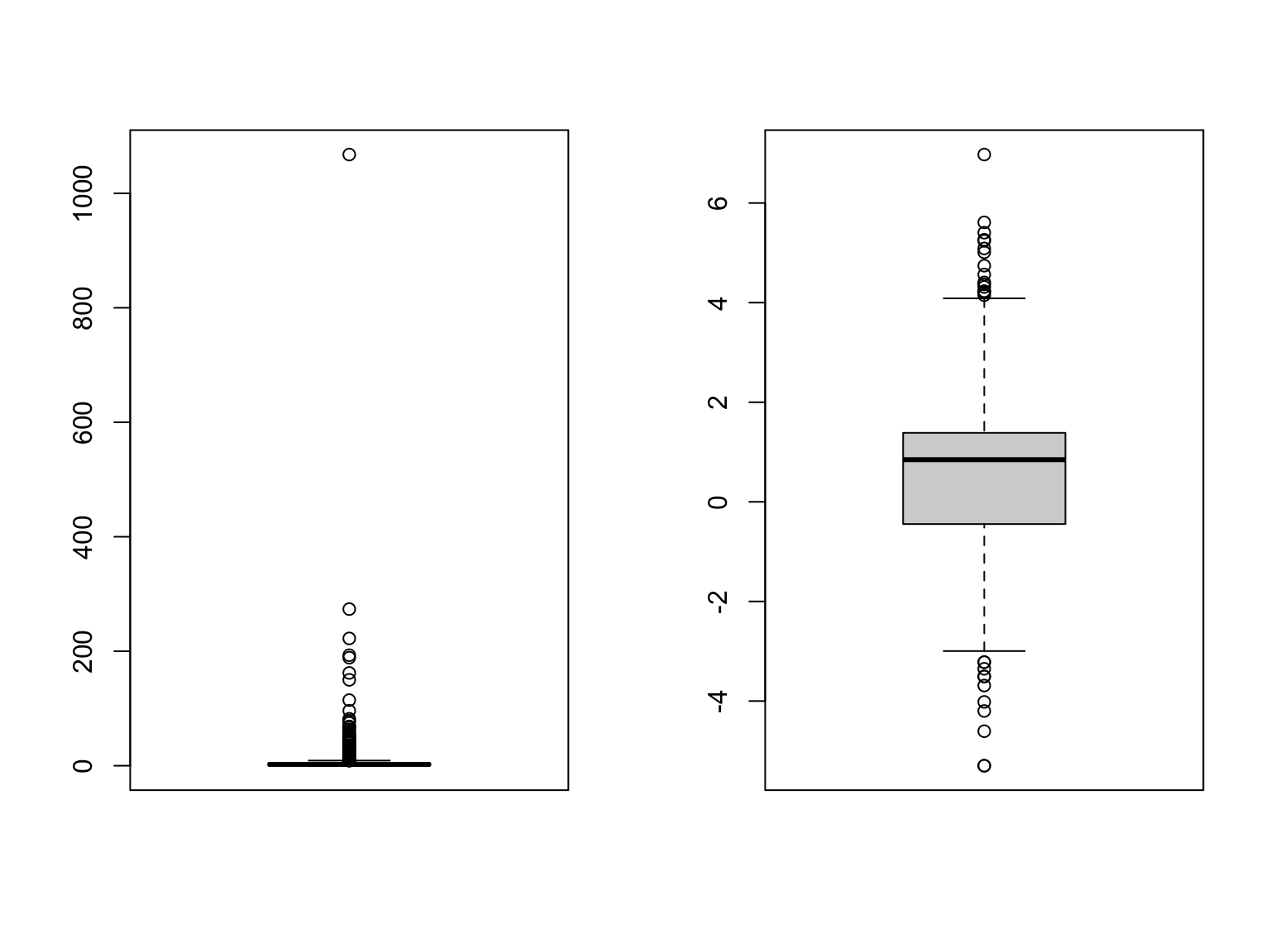

3.2.4.2 La funzione di ripartizione empirica

Una semplice idea per rappresentare graficamente un insieme di dati è quello di ottenere una versione empirica della funzione di ripartizione (o della funzione cumulata) corrispondente quindi alla analoga funzione $F(x)$ definita per una variabile aleatoria $X$.

Com’è noto per una variabile aleatoria continua $X$ la funzione di ripartizione (anche detta distribuzione cumulata di probabilità) è definita come $F(x)=Pr(X \leq x)$, ovvero fornisce la probabilità che si ottenga un valore aleatorio della $X$ inferiore o uguale a $x$.

Tale funzione è definita per $x \in \mathbb{R}$

monotona non decrescente;
pari a 0 per valori inferiori o uguali al limite inferiore del supporto della variabile $X$;
pari a 1 per valori superiori al limite superiore del supporto della variabile $X$.

Inoltre l’inversa della funzione di ripartizione fornisce i quantili per cui il quantile $x_p=F^{-1}(p)$. Ovviamente il quantile per ogni $0 \leq p \leq 1$ esiste se la funzione di ripartizione non ha discontinuità.

L’equivalente empirico di tale funzione, denotato con $\hat{F}(x)$ avendo osservato l’insieme di dati $x_1,x_2, \dots, x_n$ per una variabile quantitativa, si ottiene cercando il valore che $\forall x \in \mathbb{R}$ fornisce la proporzione di unità inferiori o pari a $x$, ovvero \[\hat{F}(x)=\mbox{proporzione}(x_i \leq x)=\frac{\mbox{numero di valori} \leq x}{n}\]

Riprendendo la notazione introdotta per i dati ordinati $x_{(1)} \leq x_{(2)} \leq \dots, \leq x_{(n-1)} \leq x_{(n)}$ la funzione di ripartizione empirica (cumulata empirica) sarà pari a:

$\hat{F}(x)=0$ se $x \leq x_{(1)}$;
in $x = x_{(1)}$ la funzione fa un salto ed è pari a $\frac{1}{n}$ e rimane costante fino al prossimo valore $x_{(2)}$;
in $x = x_{(2)}$ la funzione fa un ulteriore salto ancora di altezza $\frac{1}{n}$;
e così via fino a $x_{(n)}$ partire dal quale la funzione assume il valore 1;
se vi sono valori ripetuti il salto sarà pari a $\frac{m}{n}$ ove $m$ è il numero di valori ripetuti.

Si tratta quindi di una funzione a scalini definita come: \[\begin{equation*} \hat{F}(x)=\begin{cases} 0 & \mbox{se}~~~ x < x_{(1)} \\ \frac{i}{n} & \mbox{se}~~~ x_{(i)} \leq x < x_{(i+1)}~~~~~ \mbox{per}~~ i=1,2,\dots,n-1\\ 1 & \mbox{se}~~~ x \geq x_{(n)} \\ \end{cases} \end{equation*}\].

`E piuttosto agevole tracciare tale grafico in R. Vediamo un semplice esempio.

par(mfrow=c(1,2))
# consideriamo l'insieme di 9 dati nel vettore xx
xx<-c(148, 155, 162, 168, 172, 174, 175, 178, 186)

# rappresentiamo i punti su un grafico 
# i parametri ylim e xlim permettono di definire
# i limiti per le coordinate x e y, pch permette di scegliere il simbolo
# (4 è il simbolo X), cex le dimensioni del simbolo.
nn<-length(xx)
plot(xx,rep(0,nn), ylim=c(0,1.1), xlim=c(135,200), pch=4, cex=1.5,
     main="esempio", xlab="h=10", ylab="proporzione")
abline(0,0) 
# abline(a,b) traccia una retta con intercetta e coefficiente angolare 
# con a e b assegnati
# points() permette di aggiungere al grafico esistente nuovi punti
points(c(0,xx),c(0,1:9)/nn, pch=19)
# e il parametro type="s" consente di ottenere una funzione a gradini
plot(xx,rep(0,nn), ylim=c(0,1.1), xlim=c(140,195), pch=4, cex=1.5,
     main="esempio", xlab="h=10", ylab="proporzione")
abline(0,0) 
points(c(0,xx),c(0,1:9)/nn, type="s")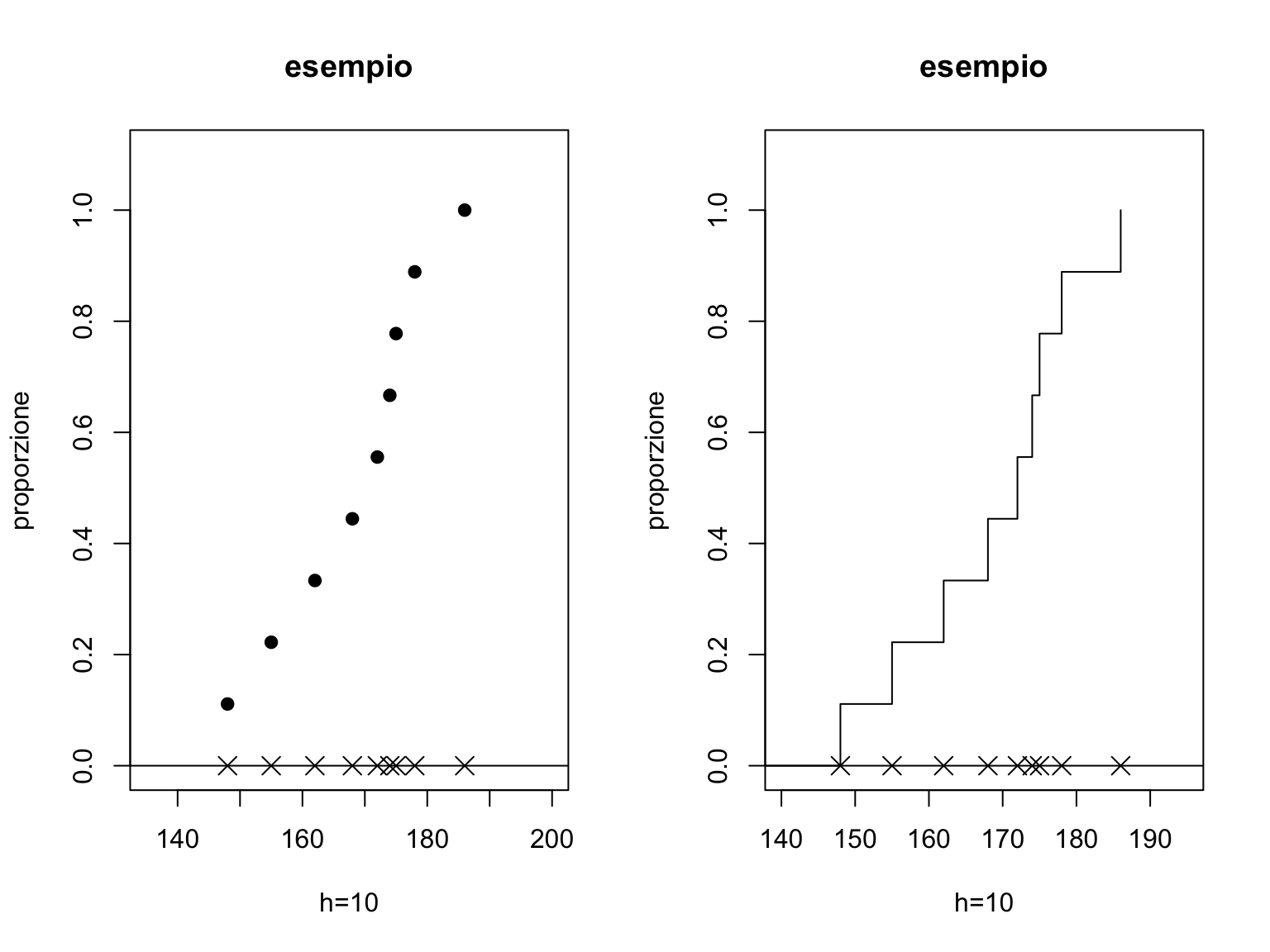

par(mfrow=c(1,1))

Come si vede la funzione ha incrementi pari a $1/n$ ogni volta che si è in corrispondenza di un nuovo dato osservato. La linea verticale nel gradino è graficamente utile ad apprezzare l’altezza dello stesso ma dal punto di vista formale la funzione dovrebbe presentarsi come una funzione costante a tratti.

Esiste la funzione ecdf predefinita in R per ottenere la funzione di ripartizione empirica. Essa consente numerose varianti e genera un oggetto che può essere direttamente fornito alla funzione plot

mio<-ecdf(xx)
plot(mio)

La funzione ecdf() è basata sulla funzione stepfun() che è appositamente costruita per trattare funzioni a gradini cui si rinvia per dettagli.

Proviamo a ottenere ora la funzione di ripartizione empirica per i dati sulla lunghezza delle auto.

plot(ecdf(Cars93$Length), main="funzione di ripartizione empirica per lunghezza",
   xlab="lunghezza", ylab="proporzione di casi")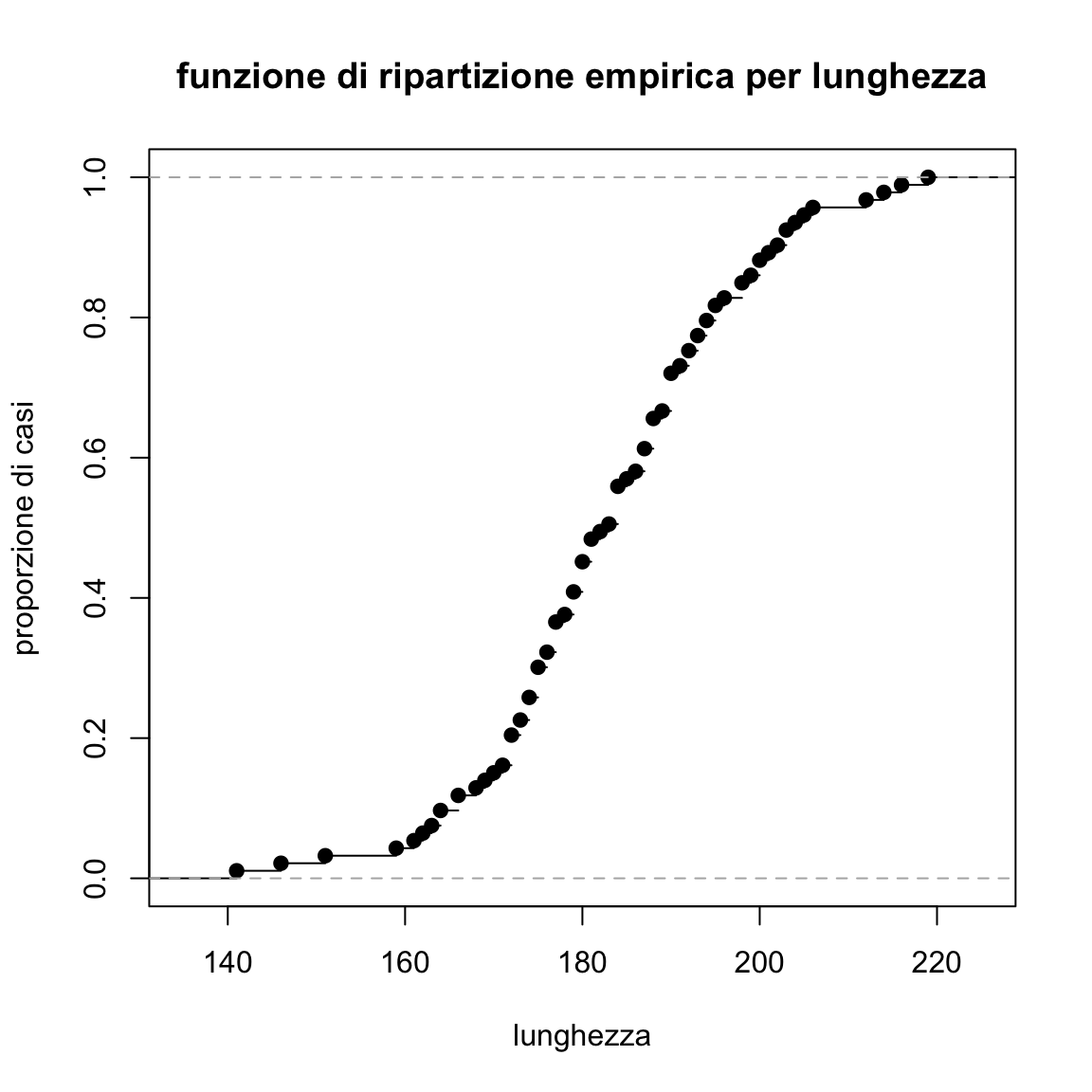

Tale rappresentazione grafica è di interesse per vari motivi:

conserva l’informazione su ogni singolo valore;
è del tutto adeguata anche con variabili quantitative discrete;
permette di visualizzare dove si trovi la mediana o alcuni percentili (la funzione dei quantili è in effetti l’inversa della funzione di ripartizione). Da questo si intende chiaramente come solo alcuni quantili sono definiti, mentre per altri occorre ricorrere ad approssimazioni (ad esempio considerando interpolazioni lineari fra i due quantili con l’ordine più prossimo);
la sua interpretazione non è agevole e immediata, ma è evidente che i punti in cui la curva cresce più veleocemente sono quelli in cui si sono osservati molti casi;
si potrebbe ricorrere a definizioni alternative (ad esempio considerando $\mbox{numero di}~~~ x_i< x$). Ottenendo una curva che sarà leggermente spostata rispetto a quella già definita ma con la stessa forma;
a partire da essa si potrebbe costruire una versione empirica della funzione di sopravvivenza $S(x)=1-F(x)$. A questa funzione occorrerebbe dedicare un capitolo a parte vista la sua rilevanza per l’analisi di dati di durata soprattutto in ambito medico (relativi, ad esempio, all’analisi dei tempi impiegati per guarire da una malattia). In effetti esistono in R pacchetti dedicati a questo;
è estremamente vantaggiosa se si vuole confrontare la distribuzione empirica con una distribuzione teorica (aspetto che verrà trattato più avanti).

Resta evidente che una più accurata rappresentazione della distribuzione dei dati si avrebbe considerando piuttosto che la versione empirica della loro funzione di ripartizione la versione empirica delle funzione di densità (che, ricordiamo, in distribuzioni di probabilità per variabili aleatorie continue sarebbe la derivata della funzione di ripartizione).

I modi per rappresentare empiricamente la funzione di densità empirica per un insieme di dati saranno oggetto dei prossimi paragrafi.

3.2.5 L’istogramma

L’istogramma è senz’altro una delle più diffuse e conosciute tecniche di rappresentazione grafica di un carattere quantitativo, i principi che ne ispirano la costruzione e l’interpretazione sono semplici e sono descritti in un qualsiasi testo di statistica di base.

L’istogramma in realtà costituisce uan forma semplice per ottenere una approssimazione empirica della funzione di densità ed è dall’estensione di tale idea che si possono poi considerare tecniche più complesse per la determinazione della curva di densità e per ottenere una versione “liscia” dell’istogramma.

Si suppone di disporre di un insieme di n dati $x_1,x_2,\ldots,x_n$ relativi ad una variabile quantitativa $X$.

Abbiamo già visto come sia possibile sintetizzare i dati di una variabile quantitativa in una tabella di frequenza: la variabile $X$ è opportunamente categorizzata e trasformata in un fattore mediante un operazione di raggruppamento in classi; si determina cioè una sequenza di valori $z_0<z_1<\ldots <z_{I-1}<z_I$ che definiscono una successione di intervalli disgiunti (classi) $(z_{i-1},z_i]$ (con $i=1,2,\ldots,I$) e si determinano le frequenze relative \[ f_i=\frac{\mbox{numero di valori nell'intervallo} (z_{i-1},z_i]}{n}. \] La rappresentazione grafica mediante istogramma della distribuzione di frequenze relative riassunta dalle I coppie $((z_{i-1},z_i],ni_i)$ si effettua costruendo dei rettangoli la cui base coincida con gli intervalli $(z_{i-1},z_i]$ e la cui altezza è tale da rendere le aree dei rettangoli proporzionali alle frequenze $n_i$. Di particolare interesse è il caso in cui le aree dei rettangoli sono pari alle frequenze relative $f_i$.

Tale risultato si ottiene introducendo il concetto di densità di frequenza relativa. L’altezza di ogni rettangolo viene quindi determinata in modo tale da consentire una corrispondenza fra l’area del rettangolo $A_i$ che insiste su $(z_{i-1},z_i]$ e la frequenza relativa $f_i$: ovvero $f_i\propto A_i$. Quindi l’altezza del rettangolo che insiste sull’intervallo $(z_{i-1},z_i]$ deve essere proporzionale a \[\begin{equation} \frac{f_i}{z_{i}-z_{i-1}}. \end{equation}\]

Di solito si calcola l’altezza così che l’area di ogni rettangolo sia pari esattamente alla frequenza relativa, così che $A_i=f_i$, e in tal caso l’area complessiva all’interno dei rettangoli che compongono il grafico risulterà pari ad 1.

Le altezze dei rettangoli sono quindi poste pari alla frequenza relativa nell’intervallo diviso per l’ampiezza dell’intervallo stesso. Esse non rappresentano quindi le frequenze relative per gli intervalli in questione bensì la densità di frequenze relative (salvo nel caso in cui le basi dei i rettangoli abbiano tutti ampiezza pari a 1), ovvero la quota di frequenze relative che insiste su un generico intervallo unitario in $(z_{i-1},z_i]$.

L’istogramma quindi rappresenta un primo, semplice, tentativo di ottenere una versione empirica della funzione di densità sottostante ai dati. Quindi \[ \hat{f}(x) \geq 0\] \[ \mbox{prop}( a \leq \mbox{units} \leq b)= \int_a^bf(x) dx\] In linea di principio possiamo calcolare il valore approssimativo della proporzione di casi fra due numeri reali $a$ e $b$ sommando le aree dei rettangoli rappresentate dall’istogramma e compresi nell’intervallo (considerando porzioni dei rettangoli se $a$ o $b$ non coincidono con gli estremi delle classi).

Come detto, attuando una suddivisione in classi si sono perse informazioni e quindi la vera proporzione di casi (che potrei ottenere solo se tornassi alle informazioni originali rinunciando al riassunto grafico) nei dati sarà verosimilmente diversa.

L’assunzione sottostante alla rappresentazione grafica è la costanza della densità nell’intervallo, ovvero su ogni sottointervallo $\Delta x$ interno a una classe di valori la frequenza relativa dipende esclusivamente dall’ampiezza $\Delta x$ (uniforme distribuzione nelle classi).

L’istogramma presenta caratteristiche che lo rendono particolarmente utile in molte situazioni applicative, ma ha anche alcuni inconvenienti.

I principali vantaggi sono:

è semplice da interpretare;
è immediato da costruire;
è facile da utilizzare.

I suoi limiti sono invece i seguenti:

il grafico presenta forti discontinuità. In particolare si potrebbe dedurre che vi è un salto fra la densità in due valori di $x$ molto prossimi ma che appartengono a due diverse classi (è ovvio che tale conclusione potrebbe essere diversa per una scelta alternativa delle classi) e talvolta (con pochi dati) il grafico potrebbe anche essere sensibilmente diverso per scelte alternative delle classi: in genere la scelta di classi più o meno ampie equivale alla scelta di un diverso grado di lisciamento e di regolarità della rappresentazione grafica;
la densità è assunta costante in ogni intervallo e tale assunto è spesso discutibile.

Ottenere un istogramma in R è semplice in quanto la funzione hist() automaticamente, determina le classi, calcola le frequenze nelle classi, e produce il grafico. ad esempio:

hist(Cars93$Length)

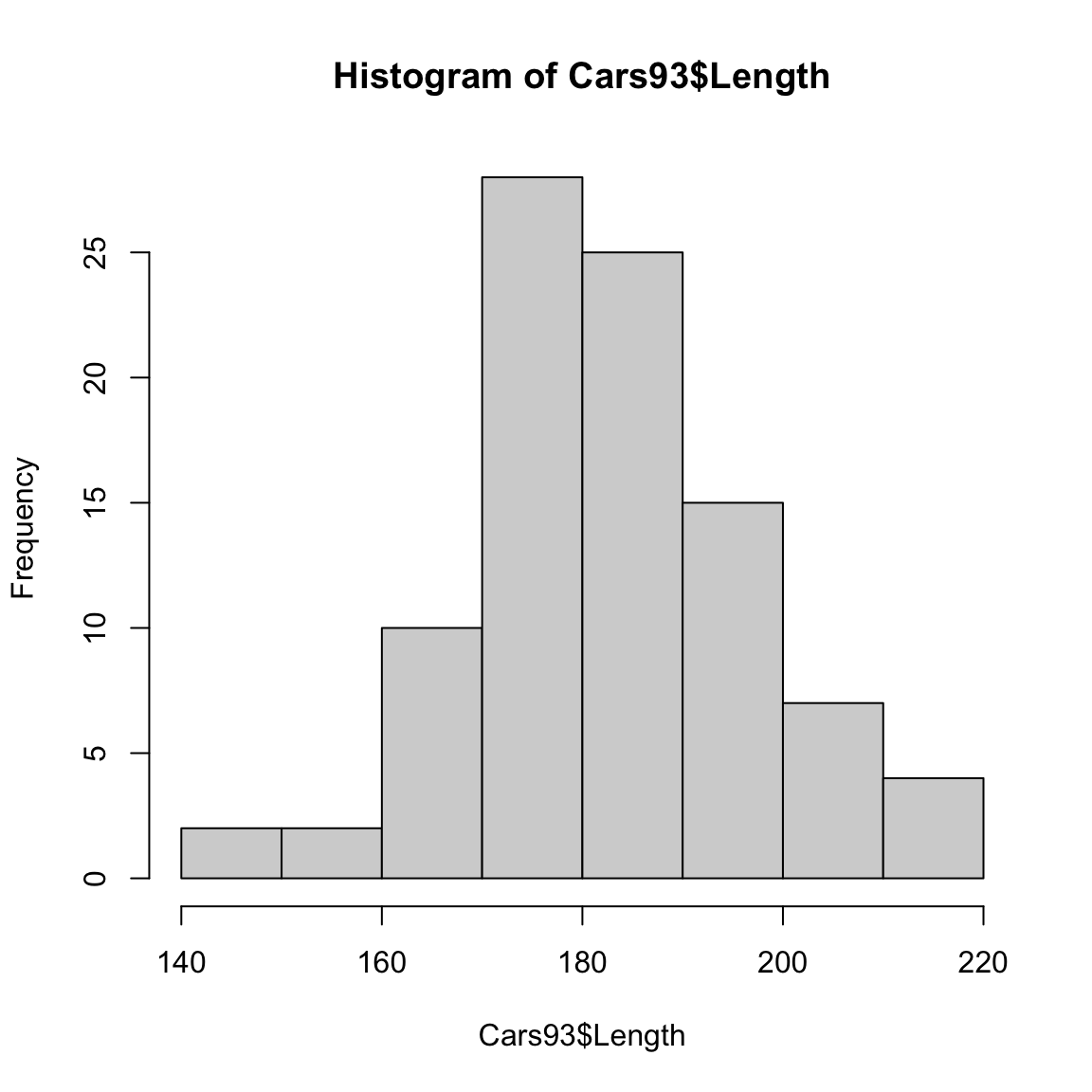
Come si vede il grafico presenta classi tutte della medesima ampiezza e presenta sull’asse i valori relativi alle frequenze assolute. Il grafico è in questo caso non rappresenta le densità, tuttavia la forma resta invariata in quanto le ampiezze delle classi sono uguali e le altezze dei rattangoli sono proporzionali alle densità.

Se si vuole però un grafico di densità, occorre specificare il parametro prob=TRUE

Il numero delle classi $M$ che vengono usate in R è determinato con una regola detta regola di Sturges per cui $M=1+\frac{log(n)}{log(2)}$. Quindi cresce (lentamente) con la dimensione del vettore di dati. E’ possibile usare regole diverse (si veda l’help della funzione hist).

Ovviamente i parametri della funzione ci consentono di variare tale scelta e anche di usare classi di ampiezza diversa. Il parametro breaks= consente di fare entrambe le cose. Gli esempi sotto che illustrano ancora quanto detto sopra: si noti come aumentando il numero delle classi si rischi di avere un grafico meno regolare troppo dipendente dalla specificita dell’insieme di dati.

par(mfrow=c(2,2))
hist(Cars93$Length, main="istogramma ottenuto usando parametri di default")
hist(Cars93$Length, prob=TRUE, main="istogramma con le densità")
hist(Cars93$Length, prob=TRUE, breaks=12, main="istogramma 12 intervalli")
hist(Cars93$Length, prob=TRUE, breaks=c(140,160,170,180,190,200,220),
     main="istogramma con classi di diversa ampiezza")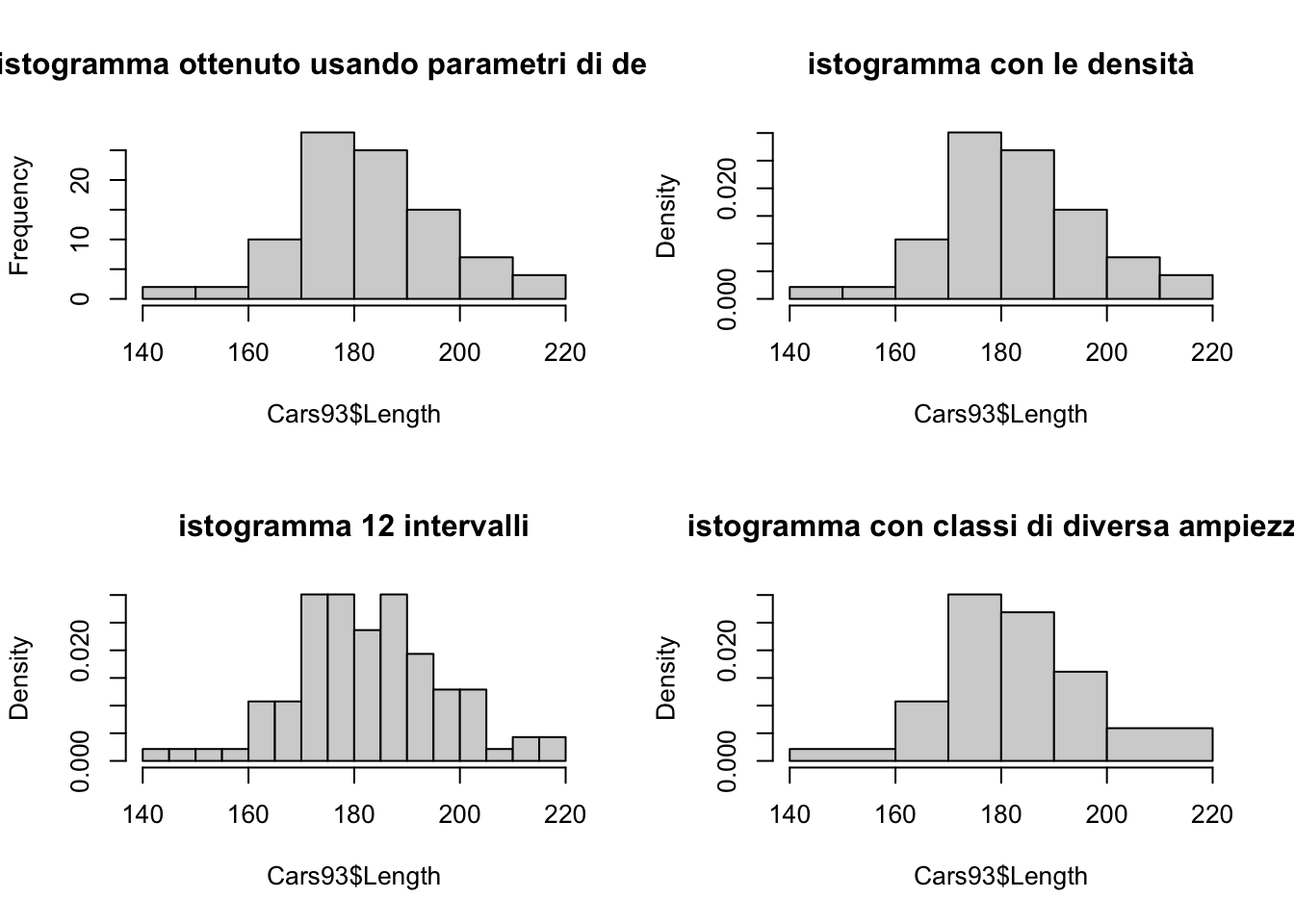

par(mfrow=c(1,1))

Per illustrare ancora quanto la rappresentazione con istogramma possa fornire grafici diversi variando alcuni criteri di costruzione, si considerino i dati geyser presenti nel package MASS. Essi si riferiscono ai tempi di attesa fra due eruzioni del geyser Old faithful nel parco di Yellowstone negli USA. Otteniamo l’istogramma

library(MASS)
data(geyser)
hist(geyser$waiting, prob=TRUE)

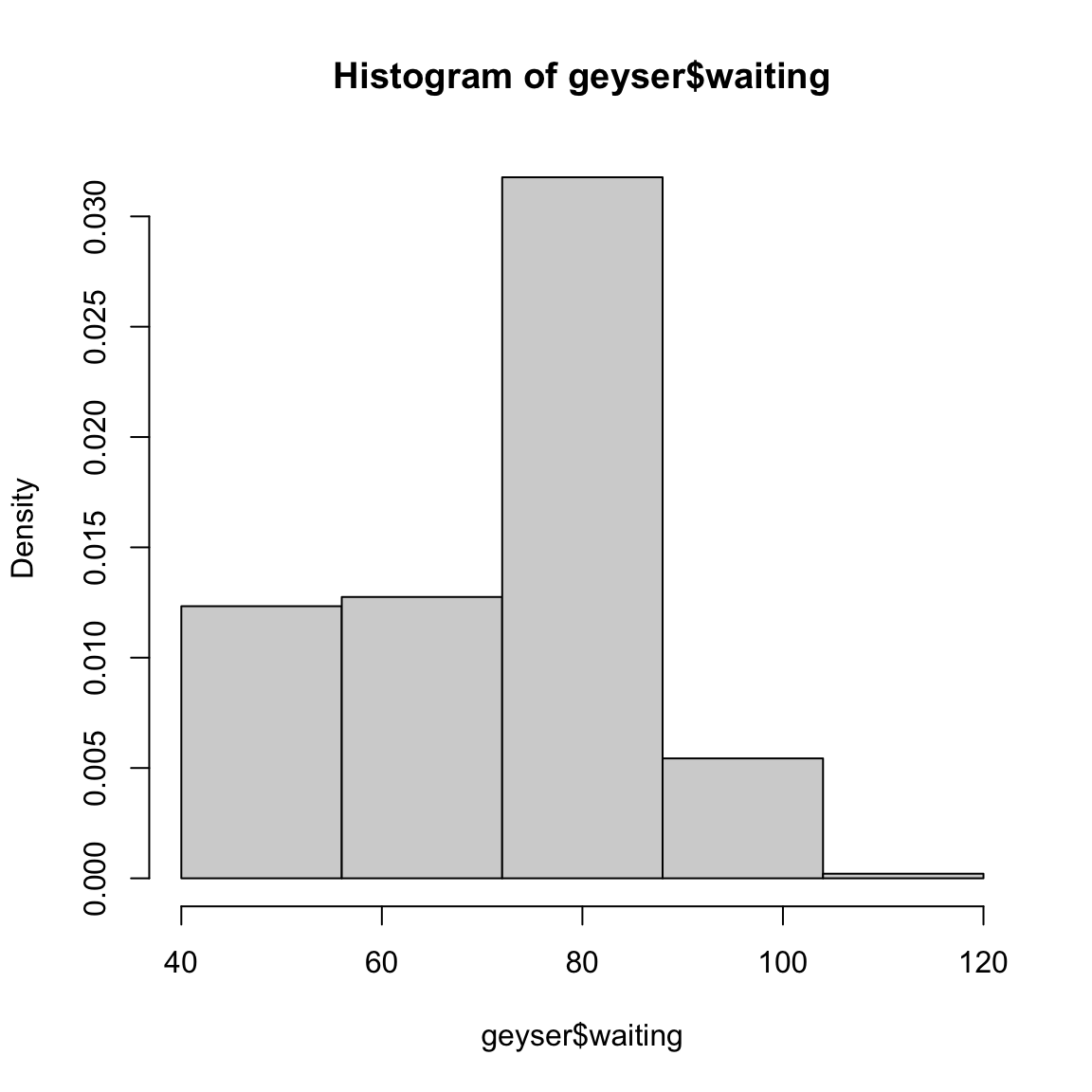
Si consideri ora una diversa suddivisione in classi mantenendo la stessa ampiezza per la variabile cambiando semplicemente l’origine della prima classe.

library(MASS)
data(geyser)
hist(geyser$waiting, breaks=c(43,(5*(1:14)+43)), prob=TRUE)

L’ampiezza delle classi è la stessa nei due casi, il punto di origine delle classi è invece spostato. Si noti che pur essendo le caratteristiche del grafico simili (entrambe le rappresentazioni grafiche consentono di cogliere le due gobbe della distribuzione), la collocazione dei due massimi nelle due gobbe e la distanza che li separa appare diversa. Se, inoltre si guarda al primo grafico si deduce che la densità di frequenza nel punto $x=72$ è la stessa che nel punto $x=74$, mentre si arriverebbe a ben altra conclusione riguardo la densità locale nei due punti se si guarda al secondo grafico.

Si noti che se utilizzassi solo 4 classi perderei la caratteristica saliente di questi dati che è data dalla presenza delle due gobbe

library(MASS)
data(geyser)
hist(geyser$waiting, breaks=c(40,56,72,88,104,120), prob=TRUE)

3.2.5.1 La moda

Nel caso di un modello probabilistico per una variabile aleatoria continua $X$ con densità $f(x)$ è possibile definire la moda Mo come \[Mo=\underset{x \in R}{\arg \max}f(x)\] ovvero il valore cui corrisponde la densità più alta.

La moda è un indice di tendenza centrale e, ovviamente, essa risulta definita anche per una variabile aleatoria discreta: in questo caso si tratta di determinare il valore del supporto della variabile aleatoria cui corrisponde la probabilità più elevata.

La versione empirica della moda, calcolata per un insieme di dati, è quindi definita nei diversi casi come segue:

nel caso di una variabile categoriale (un fattore) essa è definita come la modalità cui corrisponde la frequenza relativa più elevata nel collettivo esaminato. La moda rappresenta l’unico indice di tendenza centrale, che è possibile determinare per una variabile categoriale.
nel caso di una variabile quantitativa discreta essa è definita come il valore cui corrisponde la frequenza più elevata;
nel caso di una variabile quantitativa continua, essa si può definire dopo la trasformazione della variabile in fattore utilizzando il raggruppamento in classi. In tal caso si determina la classe modale che è quella classe cui corrisponde la densità di frequenza più elevata (si noti che non si guarda in questo caso alla semplice frequenza nella classe se le classi hanno ampiezza diversa).

È interessante notare che se si vuole determinare la moda di una variabile categoriale (o anche di una variabile quantitativa discreta) non esiste una funzione predefinita in R, come ad esempiomean()o median(), rispettivamente per media e mediana, occorre definire una funzione apposita. Sotto si fornisce un esempio:

moda1<-function(x){
t<-table(x)
return(labels(t[t==max(t)]))
}
# se ora si considera un vettore categoriale
pp<-c("A","A","A","A","B","B","A","C","A","C","B","B")
table(pp)

## pp
## A B C 
## 6 4 2

# si vede che la moda è "A" e, in effetti,
moda1(pp)

## [1] "A"

# proviamo con una variabile quantitativa discreta
po<-rpois(100,3)
table(po)

## po
##  0  1  2  3  4  5  6  7 
##  8 24 22 21 13  9  2  1

# si vede che la moda è pari a 3
moda1(po)

## [1] "1"

Nel caso di variabili quantitative (continue o discrete), essendo la moda il valore cui corrisponde il punto di massimo assoluto per la funzione che rappresenta la densità (o la frequenza), si possono talvolta reperire altri valori però corrispondenti a punti di massimo relativo (mode secondarie). Se una distribuzione oltre alla moda principale (quella per cui si osserva il massimo assoluto) mostra una o più mode secondarie si parla di distribuzione multimodale (bimodale, ad esempio, se i punti di massimo sono due).

Si noti che in distribuzioni unimodali la posizione della moda rispetto alla mediana e alla media fornisce indicazioni sulla asimmetria della distribuzione. In distribuzioni simmetriche i tre indici sono circa nella stessa posizione, mentre se c’è asimmetria positiva (coda destra lunga) si ha $Mo<Me<M$. L’ordinamento si inverte nel caso di asimmetria negativa.

Nel caso dei dati del geyser visti sopra la distribuzione presenta una evidente bimodalità.

3.2.6 Il metodo del nucleo per il “lisciamento” di una curva di densità

A partire dalla definizione di densità di frequenza introdotta per l’istogramma è possibile ottenere la densità di frequenza relativa locale in un qualsiasi punto $x$ come

\[\begin{equation} d(x)=\frac{numero \ di \ valori \ in \ (x-\frac{h}{2}; \, x+\frac{h}{2}]}{hn} \tag{3.1} \end{equation}\]

`E come se si prendesse una classe di ampiezza $h$ e la si muovesse ponendola in corrispondenza di ciascun valore osservato

Si potrebbe quindi tracciare il grafico della curva $d(x)$, osservando che essa risulterà avere delle discontinuità nei punti $x_i\pm \frac{h}{2}$ e sarà costante nei tratti intermedi. L’inconveniente legato alle discontinuità presenti nel grafico, peraltro meno rilevanti se $n$ è grande, può essere tuttavia superato come si vedrà nel successivo paragrafo.

La funzione $d(x)$ quindi associa ad ogni valore $x$ la densità di frequenze relative misurata con riferimento ad un intervallo di ampiezza $h$ centrato su $x$. La curva di densità che descrive tale funzione è uno strumento utile per l’analisi di un insieme di dati quantitativi: come per l’istogramma, esso fornisce infatti una rappresentazione grafica di immediata comprensione. Dove la densità di frequenza è elevata il numero di unità che insiste sull’intervallo di ampiezza $h$ centrato su $x$ è maggiore che in punti ove la densità risulta minore. Si ha in definitiva uno sguardo sull’intera distribuzione di valori senza tuttavia dover imporre come per l’istogramma una particolare scelta di classi di valori.

Per esempio, usando tale criterio (con h=10) per i dati sulla lunghezza delle auto si otterrebbe:

par(mfrow=c(1,2))
# versione della densità ottenuta applicando la definizione in (2) 

nucl<-function(x,xx,h=1) {
  y=0
  n=length(xx)
  nucl=0
  for (i in 1:n){
    nucl=nucl+(abs(x-xx[i]) <= h/2)*1/(n*h)}
  nucl
}
plot(sort(Cars93$Length),nucl(sort(Cars93$Length),Cars93$Length,10),
     cex=.5, pch=19, ylab="Lenght", xlab="densità")

# versione del grafico in cui il calcolo viene fatto per tutti 
# i punti di x e non solo in quelli osservati

plot(seq(130,230),nucl(seq(130,230),Cars93$Length,10), lwd=1.5,
     type="s", ylab="Lenght", xlab="densità")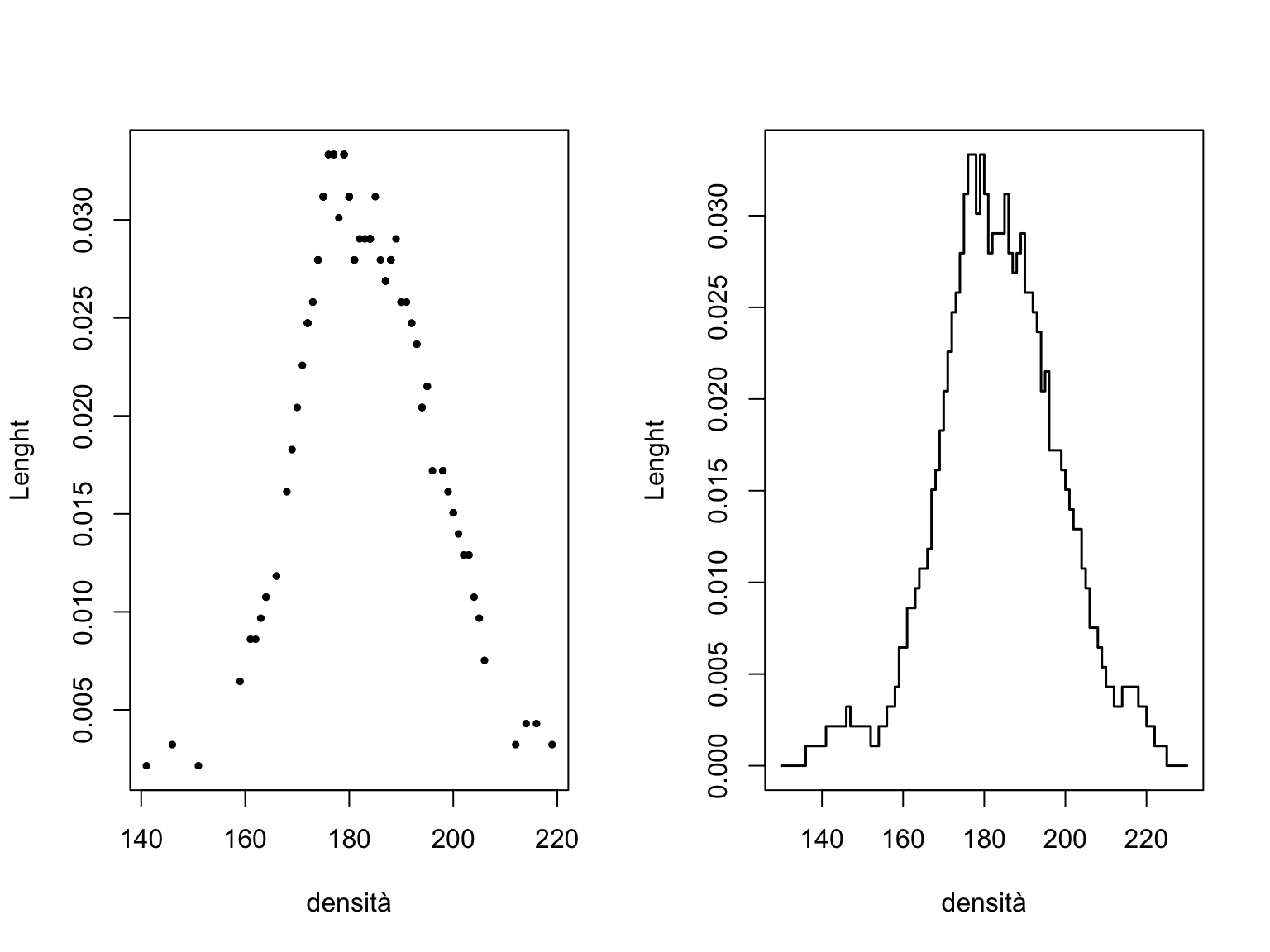

par(mfrow=c(1,1))

I valori di densità che descrive tale funzione forniscono uno strumento utile per l’analisi di un insieme di dati quantitativi: come per l’istogramma, esso fornisce infatti una rappresentazione grafica di immediata comprensione. Dove la densità di frequenza è elevata il numero di unità che insiste sull’intervallo di ampiezza $h$ centrato su $x$ è maggiore che in punti ove la densità risulta minore. Si ha in definitiva uno sguardo sull’intera distribuzione di valori senza tuttavia dover imporre come per l’istogramma una particolare scelta di classi di valori.

Si noti che tracciare un istogramma equivale alla determinazione della densità secondo la definizione introdotta nella (3.1) sopra solo per i punti $x$ al centro degli intervalli $x=\frac{z_{z-i}+z_{i}}{2}$. La particolarità è che tale valore della densità viene estesa a tutti i valori $x\in(z_{i-1};z_i]$. L’istogramma è quindi una soluzione molto particolare e non del tutto efficiente del problema di determinare la funzione di densità di frequenza $d(x)$.

3.2.6.1 Determinazione di una funzione di densità empirica con il metodo del nucleo

Al fine di superare alcuni degli inconvenienti già citati nel caso dell’istogramma è quindi possibile approssimare la curva di densità semplicemente applicando la definizione (3.1).

La (3.1)} può essere opportunamente riscritta come segue. Si definisca \[\begin{equation*} W(x)=\begin{cases} 1 & \mbox{se}~~~ |x| < \frac{1}{2} \\ 0 & \mbox{altrimenti} \end{cases} \end{equation*}\] allora \[\begin{equation} d(x)= \frac{1}{n} \sum_{i=1}^{n} \frac{1}{h} W \left(\frac{x-x_i}{h}\right) \tag{3.2} \end{equation}\]

La (3.2) è equivalente alla (3.1) ma, come vedremo, rende naturale l’estensione e la generalizzazione di quest’ultima.

Come già notato la curva che si ottiene con la (3.1) è discontinua nei punti $x_i\pm\frac{h}{2}$, ove $x_i$ è un generico valore corrispondente ad uno dei dati osservati, anche se l’entità delle discontinuità è ridotta rispetto a quello che accade con l’istogramma. Ciò è dovuto alla discontinuità della funzione $W$.

In realtà la formulazione in (3.2) equivale ad assumere che l’impatto sulla curva di densità di un qualsiasi valore $x_i$ sia distribuito in ugual misura con peso $\frac{1}{h}$ su tutto l’intervallo $(x-\frac{h}{2};x+\frac{h}{2}]$, cosicchè comunque il peso complessivo di ogni singola osservazione $x_i$ sia pari a $\frac{1}{n}$.

La funzione $W(u)$ è un rettangolo di ampiezza $h$ ed il calcolo nella (3.2)} equivale a posizionare un rettangolo di ampiezza $h$ in corrispondenza di ogni valore osservato $x$, a valutare la frequenza relativa dei casi che sono all’interno dell’intervallo e a determinare la densità di frequenze relative in $x$ come il rapporto fra la frequenza relativa ottenuta e l’ampiezza dell’intervallo stesso.

Una interpretazione equivalente si ha immaginando di posizionare una scatola di ampiezza $h$ e altezza $\frac{1}{n}$ in corrispondenza di ogni dato osservato $x_i$, in modo che il centro della scatola coincida con $x_i$. Il valore di $d(x)$ è pari alla somma delle altezze di tutte le scatole che comprendono il valore $x$ diviso per $n$.

Illustriamo quanto detto nel seguente esempio

par(mfrow=c(1,1))
# consideriamo ancora l'insieme di 9 dati nel vettore xx
xx<-c(148, 155, 162, 168, 172, 174, 175, 178, 186)

plot(xx,rep(0,9), ylim=c(0,0.065), xlim=c(135,200), pch=4, cex=1.5,
     main="esempio", xlab="h=10", ylab="densità")
abline(0,0)

# infine rappresentiamo le funzioni W, ovvero dei rettangoli centrati su ciascun dato
yc=0
for (i in 1:9){
yc[i]<- jitter(1/180) #la funzione jitter() consente di spostare un dato
                     #di una piccola quantità, è utile per rappresentare
                    # dati che apparirebbero altrimenti sovrapposti
segments(xx[i]-10,yc[i],xx[i]+10,yc[i], col=(i+1), lwd=3) # la funzione segments
                                  # aggiunge una linea su un grafico fra                                                   # due punti di coordinata data
segments(xx[i]-10,0,xx[i]-10,yc[i], col=(i+1),lwd=2, lty=2)
segments(xx[i]+10,0,xx[i]+10,yc[i], col=(i+1),lwd=2, lty=2)}

# Successivamente costruiamo una funzione che calcoli per ogni x
# la somma delle ordinate delle funzioni W(x) (la somma delle altezze
# dei rettangoli di ampiezza h)

rett<-function(x,xx,h=1) {
  n=length(xx)
  rett=0
  for (i in 1:n){
    rett=rett+(abs(x-xx[i]) <= h/2)*1/(n*h)}
  rett
}

# ora sovrapponiamo al grafico: la funzione points() permette di aggiungere
# punti su un grafico esistente
xr<-seq(135,200,.5)
points(xr,rett(xr,xx,20), lwd=2.5, type="s")

# aggiungiamo un altro esempio con rettangoli più ampi
points(xr,rett(xr,xx,20), lwd=2, type="s", col=2,
  main="esempio con rettangoli più ampi", ylab="h=20", xlab="densità")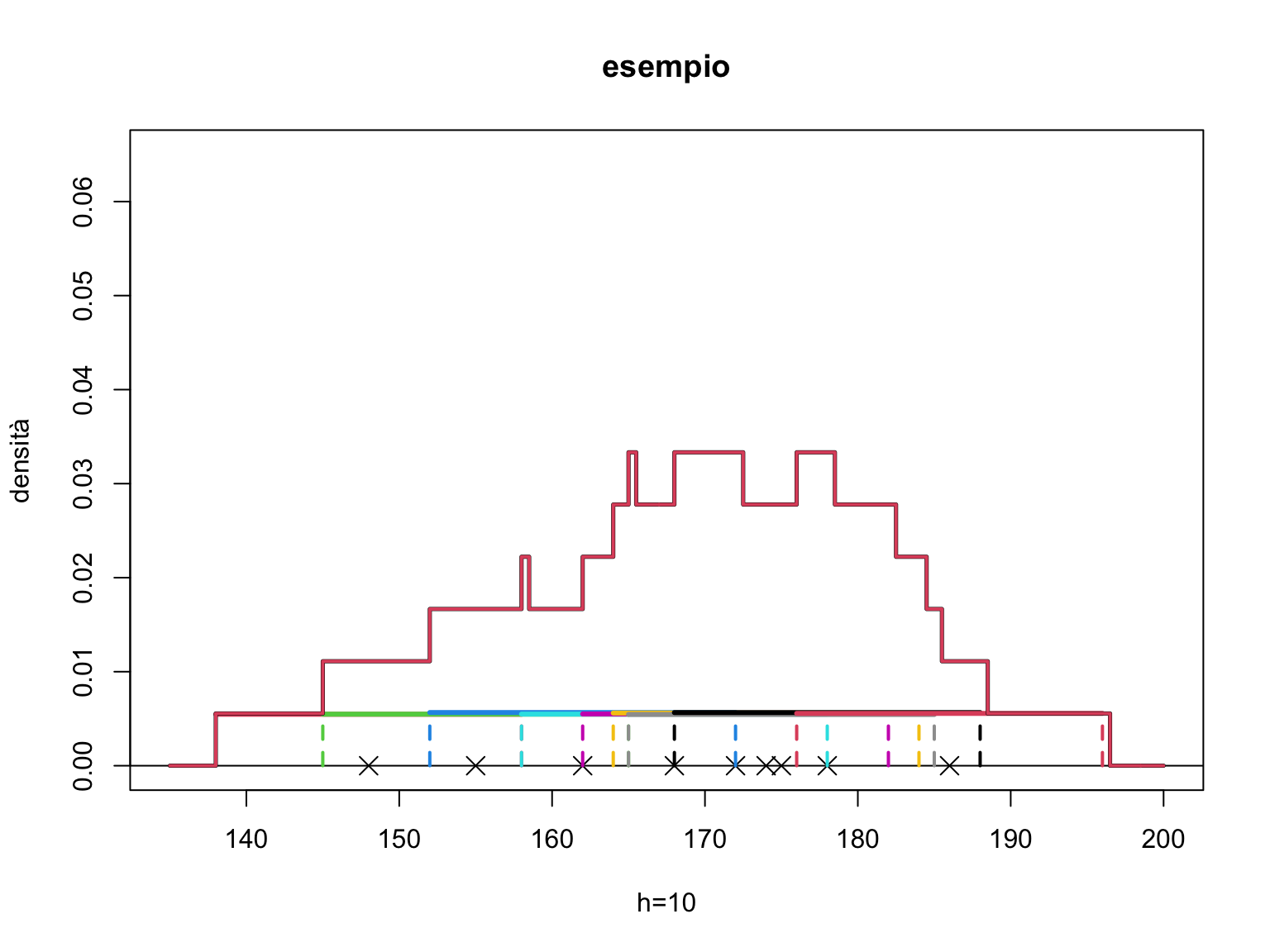

Una naturale estensione della (3.2) si ha se si assume che ogni singolo dato osservato $x_i$ abbia un impatto sulla densità in $x$ decrescente con la distanza $x-x_i$. Ciò implica che ad esempio si possa usare una funzione per $W(u)$ diversa dal rettangolo.

In generale possiamo introdurre una funzione $K(u)$, detta nucleo, che abbia le seguenti caratteristiche

$\int^{-\infty}_{\infty} K(u) du=1,$
$K(u)$ è una funzione simmetrica rispetto a 0,
$K(u)$ assume solo valori positivi.

E la funzione $d(x)$ avendo osservato un insieme di dati viene determinata come \[\begin{equation} d(x)= \frac{1}{nh} \sum_{i=1}^{n} K \left (\frac{x-x_i}{h}\right). \tag{3.3} \end{equation}\]

Si noti che la funzione $W(u)$ definita precedentemente ha le caratteristiche di una funzione nucleo. Altre scelte ragionevoli per $K(u)$ sono, ad esempio le seguenti: \[\begin{equation*} K(u)=\begin{cases} \frac{3}{4}(1-\frac{1}{5}u^2) 5^{-\frac{1}{2}} & \mbox{se} |u|<5\\ 0 & \mbox{altrimenti} \end{cases} \end{equation*}\]

\[\begin{equation*} K(u)=\begin{cases} 1+cos2\pi & \mbox{se} |u|< 0.5 \\ 0 & \mbox{altrimenti} \end{cases} \end{equation*}\] \[\begin{equation*} K(u)= \frac{1}{\sqrt{2\pi}}e^{-\frac{u^2}{2}}. \end{equation*}\]

L’ultima funzione è facilmente identificabile come una funzione di densità di una normale standard (nucleo gaussiano). L’interpretazione della (3.3) data per la funzione $W(u)$ (detta nucleo rettangolare) è valida anche in questo caso, basti pensare che in corrispondenza di ogni osservazione $x_i$ stavolta si posiziona invece che una scatola un cumulo centrato su $x_i$ la cui forma è data da una delle funzioni nucleo descritte precedentemente divise per $hn$. Il valore di $d(x)$ è pari alla somma del valore dell’ordinata di ciascuna degli n cumuli.

Riconsideriamo i dati dell’esempio precedente e utilizziamo il nucleo gaussiano. Nel grafico rappresentiamo delle piccole gaussiane (che hanno area sottostante pari a $1/n$) centrate su ciascun dato. La curva che si ottiene è pari, per ogni valore $x$, alla somma delle ordinate in $x$ di ciascun nucleo.

par(mfrow=c(1,1))

xx<-c(148, 155, 162, 168, 172, 174, 175, 178, 186)
plot(xx,rep(0,9), ylim=c(0,0.065), xlim=c(135,200), pch=4, cex=1.5,
     main="esempio", xlab="h=4", ylab="densità")
abline(0,0)

# rappresentiamo le funzioni K, come delle guassiane divise per n
n=length(xx)
for (i in 1:n){
  curve(dnorm(x,xx[i],4)/n, col=(i+1), lwd=3, lty=2, add=TRUE)}

# Successivamente costruiamo la funzione che calcoli per
# ogni x la somma delle ordinate delle funzioni K (la somma
# delle altezze delle gaussiane)

nuclg<-function(x,xx,h=1) {
  nucl=0
  nn<-length(x)
  n=length(xx)
  for (i in 1:nn){
  nucl[i]= sum(dnorm(x[i],xx,h)/n)}
  nucl
}
lines(xr,nuclg(xr,xx,4),lwd=2.5)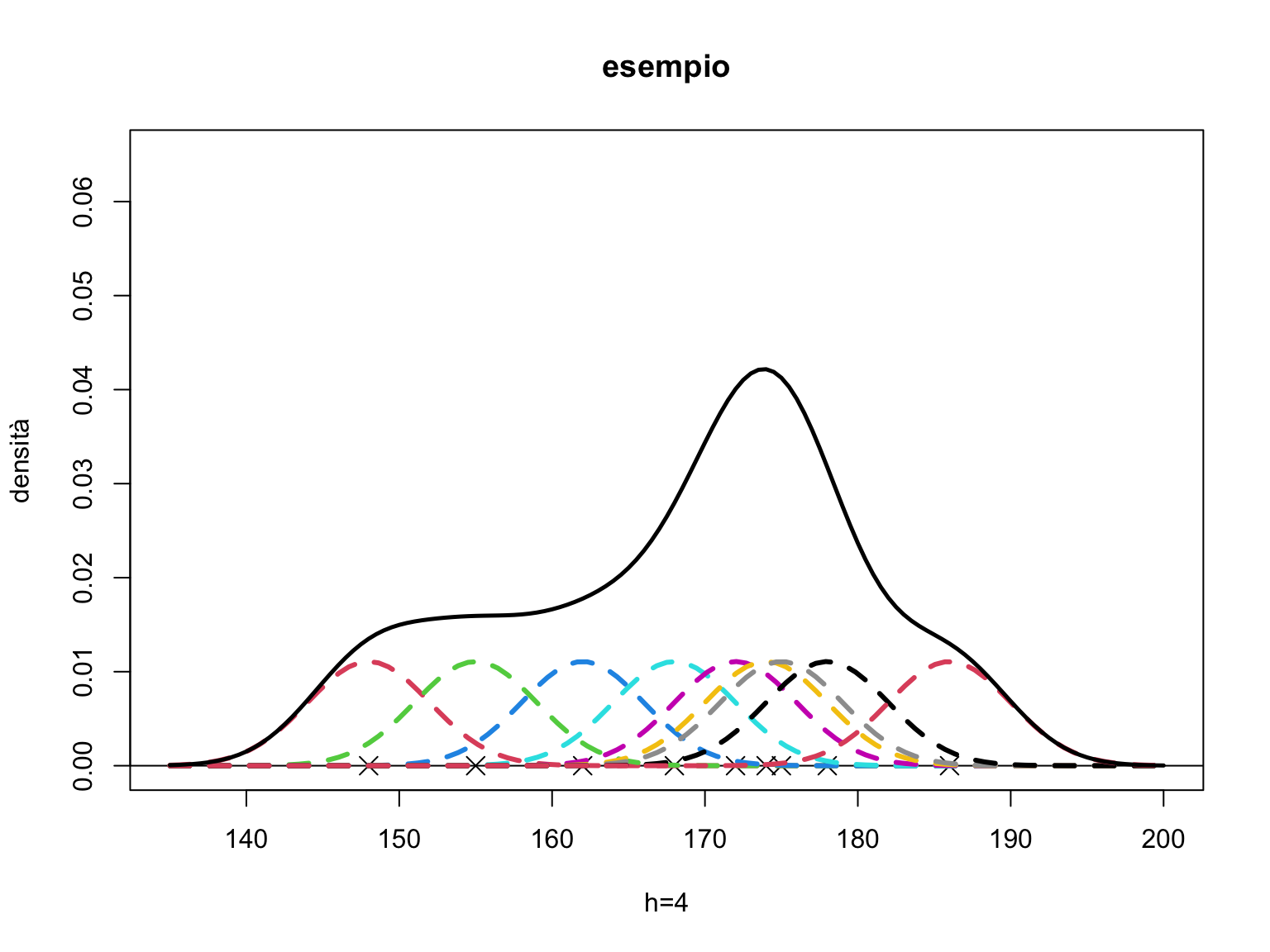

3.2.6.2 Il parametro di lisciamento

Il comportamento della funzione $d(x)$ ottenuta impiegando la (3.3) eredita alcune delle proprietà del nucleo utilizzato. In particolare, se $K(u)$ è essa stessa una funzione di densità come nel caso visto del nucleo gaussiano, allora:

Il grado di lisciamento della curva $d(x)$ dipende tuttavia dal valore di $h$ che è appunto detto parametro di lisciamento. Infatti come si deduce dalla formula (3.3), $h$ è un fattore di scala che compare fra gli argomenti della funzione $K$. Valori di $h$ grandi implicano un impatto su $d(x)$ di un generico dato $x_i$ anche per valori molto distanti da esso mentre valori di $h$ piccoli fanno sì che il peso di $x_i$ abbia un ruolo nel determinare il valore di $d(x)$ solo quando $x$ non è molto distante da $x_i$ stesso.

Riprendiamo l’esempio visto e otteniamo le densità ottenute con il metodo del nucleo con tre diversi valori di lisciamento diversi.

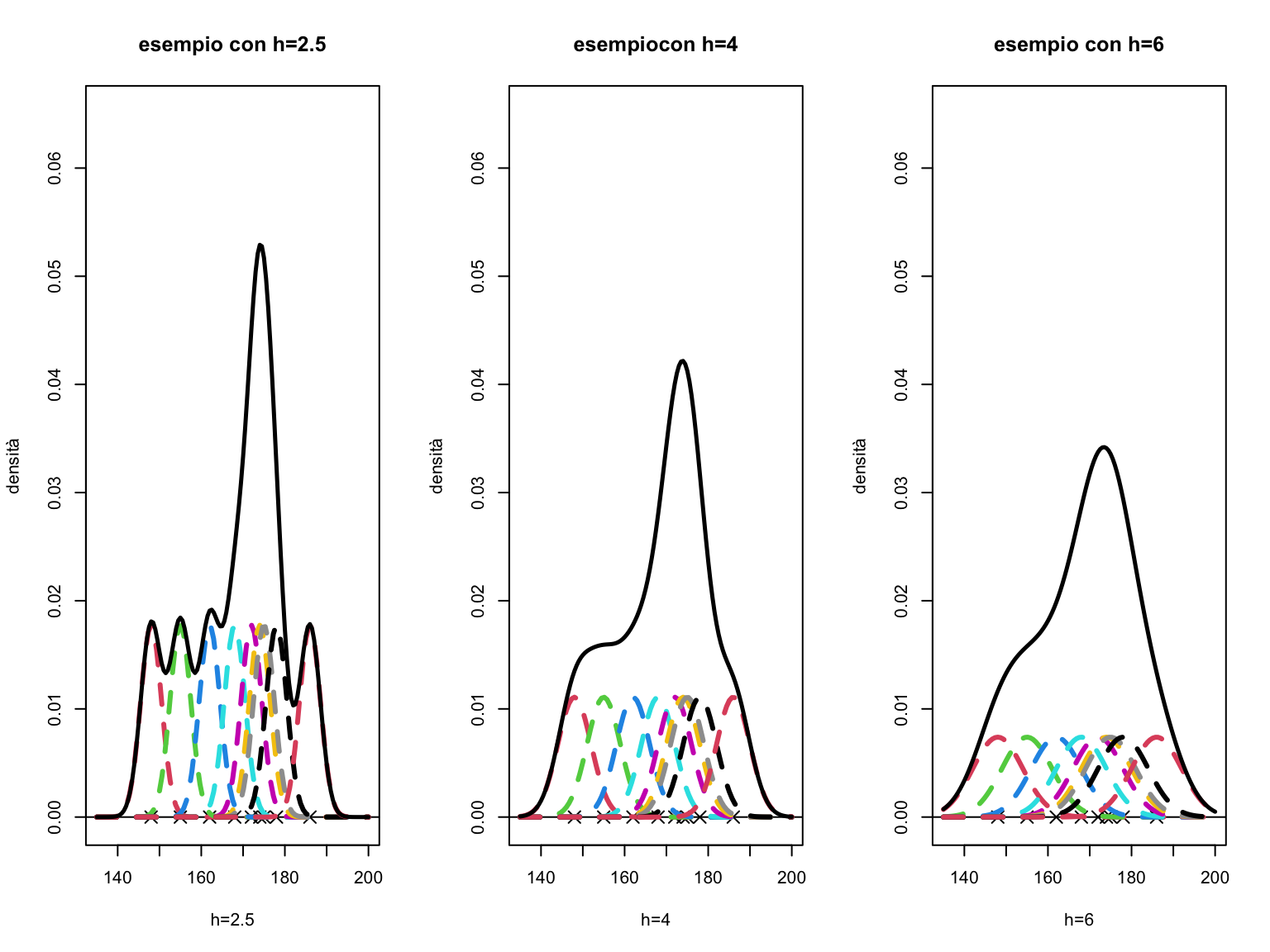
La figura a destra con $h$ è più piccolo e con nuclei più appuntiti dà come risultato risultato una curva meno liscia. L’opposto vale per la figura a destra ove i nuclei troppo ampi nascondono le variazioni della densità in alcune aree.

La scelta di $h$ dipende da considerazioni analoghe a quelle fatte per la scelta dell’ampiezza delle classi nel caso dell’istogramma. Un valore del parametro di lisciamento piccolo rischia di introdurre un alto numero di brusche variazioni nella curva di densità in particolar modo nelle regioni dove si osservano pochi dati mentre un valore alto di $h$ permette di determinare una funzione liscia al prezzo di oscurare caratteristiche locali della curva di densità (ad esempio nascondendo effettive caratteristiche bimodali della distribuzione dei dati).

R contiene alcune funzioni che consentono il calcolo della curva di densità, e a partire da questo produca un grafico della curva di densità scegliendo un appropriato nucleo e il valore di $h$ opportuno (in R il parametro di lisciamento è denotato con bw riferito al termine bandwidth) .

In particolare, se si vuole un grafico della densità con il metodo del nucleo si può utilizzare la funzione density(). In essa il grado di lisciamento viene controllato mediante il parametro bw= ed è anche possibile scegliere funzioni nucleo alternative (il default è il nucleo gaussiano anche se va detto che, in genere, la scelta del nucleo è meno cruciale rispetto a quella del parametro di lisciamento).

Vediamo cosa accade usando tale funzione con i dati geyser.

par(mfrow=c(1,1))

den<-density(geyser$waiting)
plot(den, main="tempi di attesa fra successive eruzioni")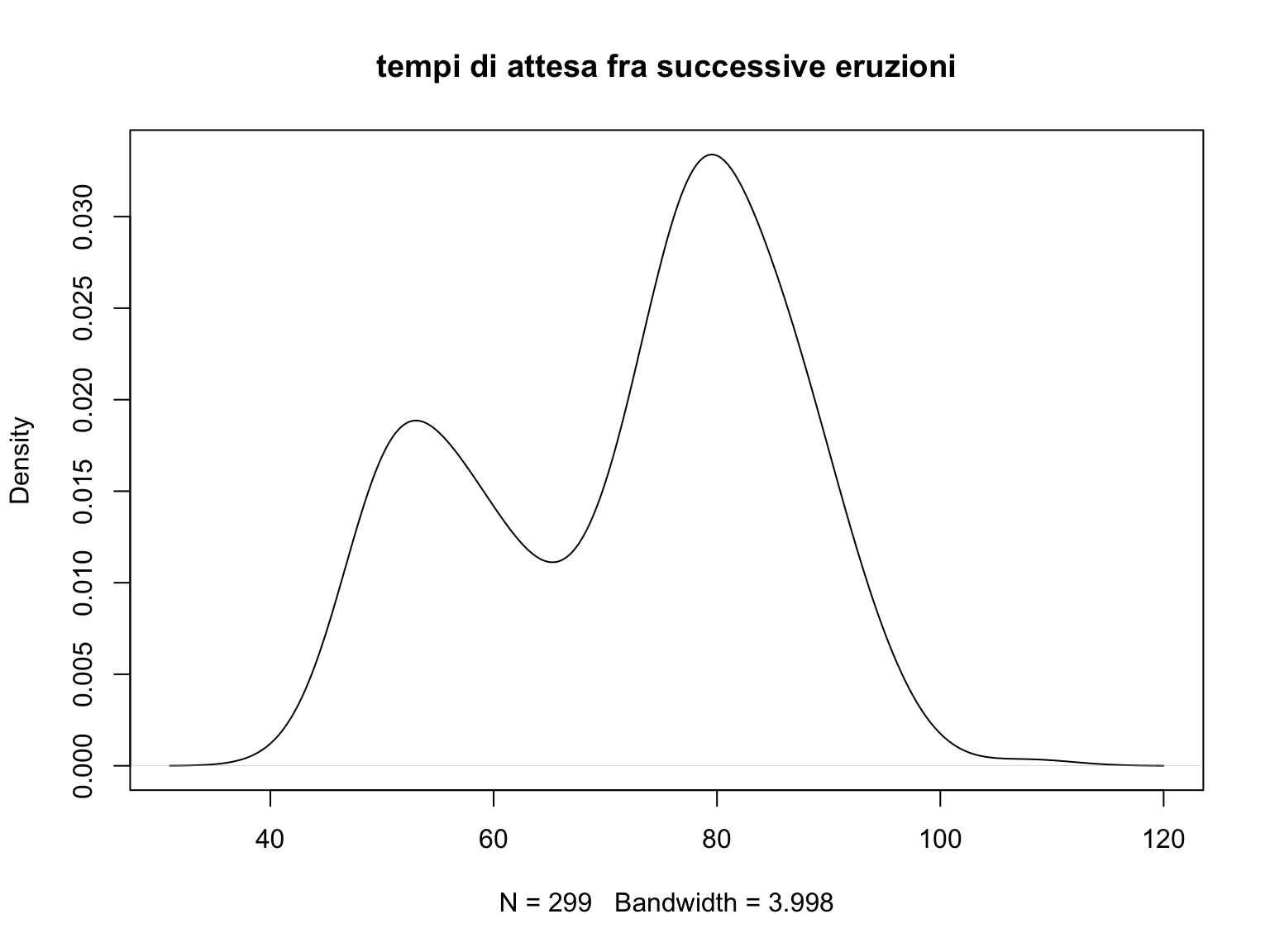

# Nel grafico è riportato il valore del parametro di lisciamento.
# La funzione density() potrebbe quindi essere chiamata direttamente
# all'interno di altre funzione come la plot() per ottenere il grafico
# della curva di densità.
# Si guardi cosa accade se si varia il parametro di lisciamento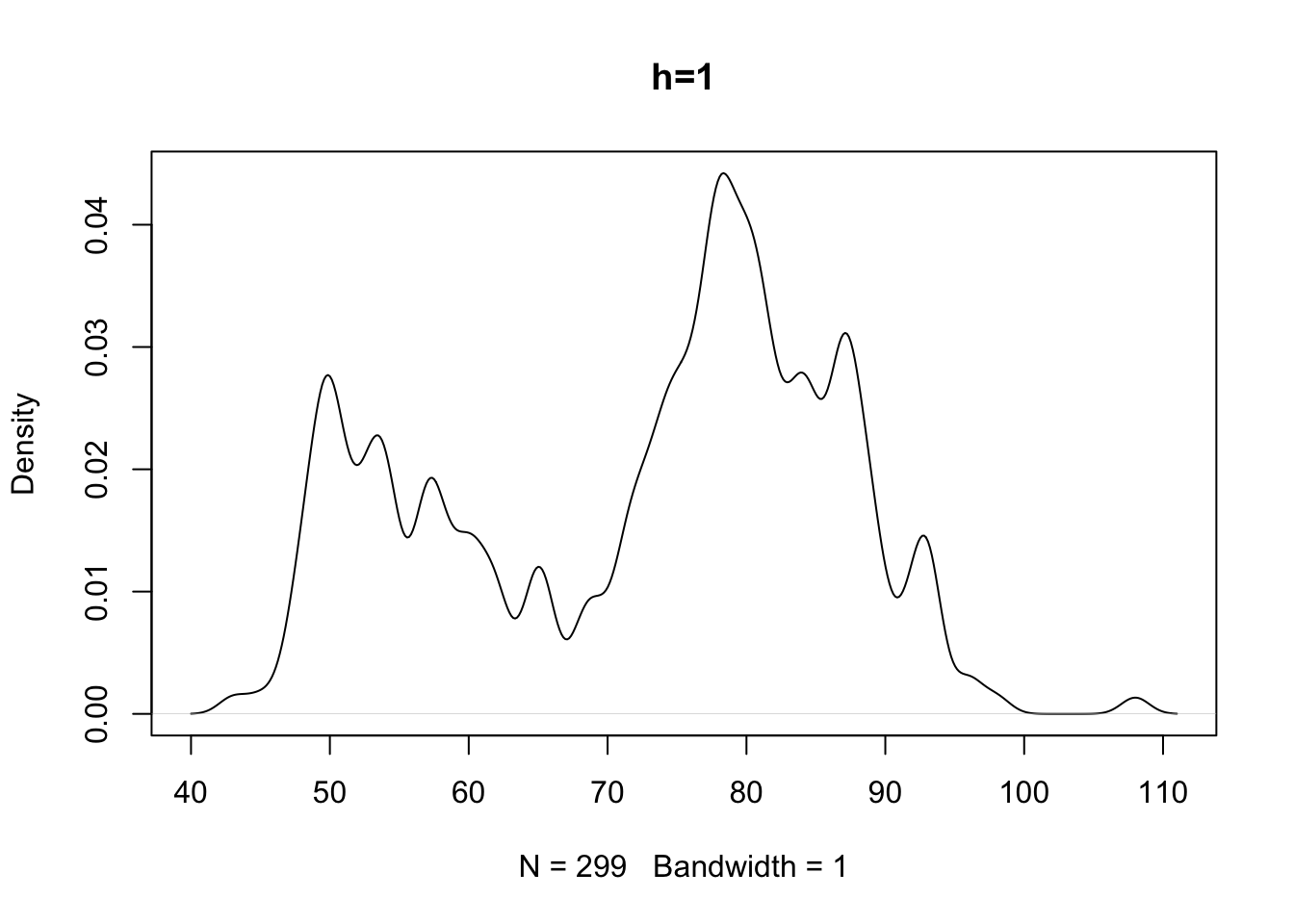

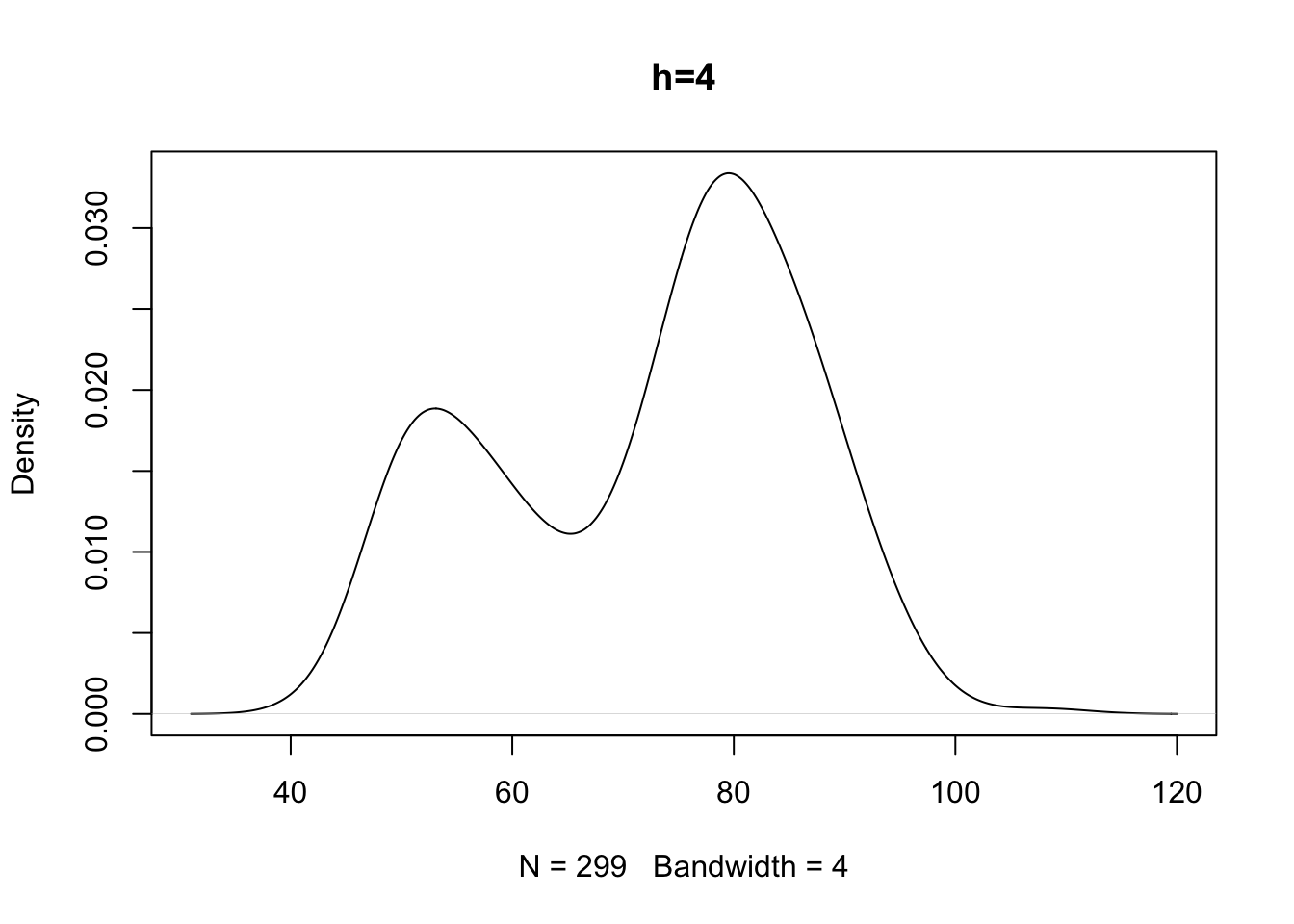
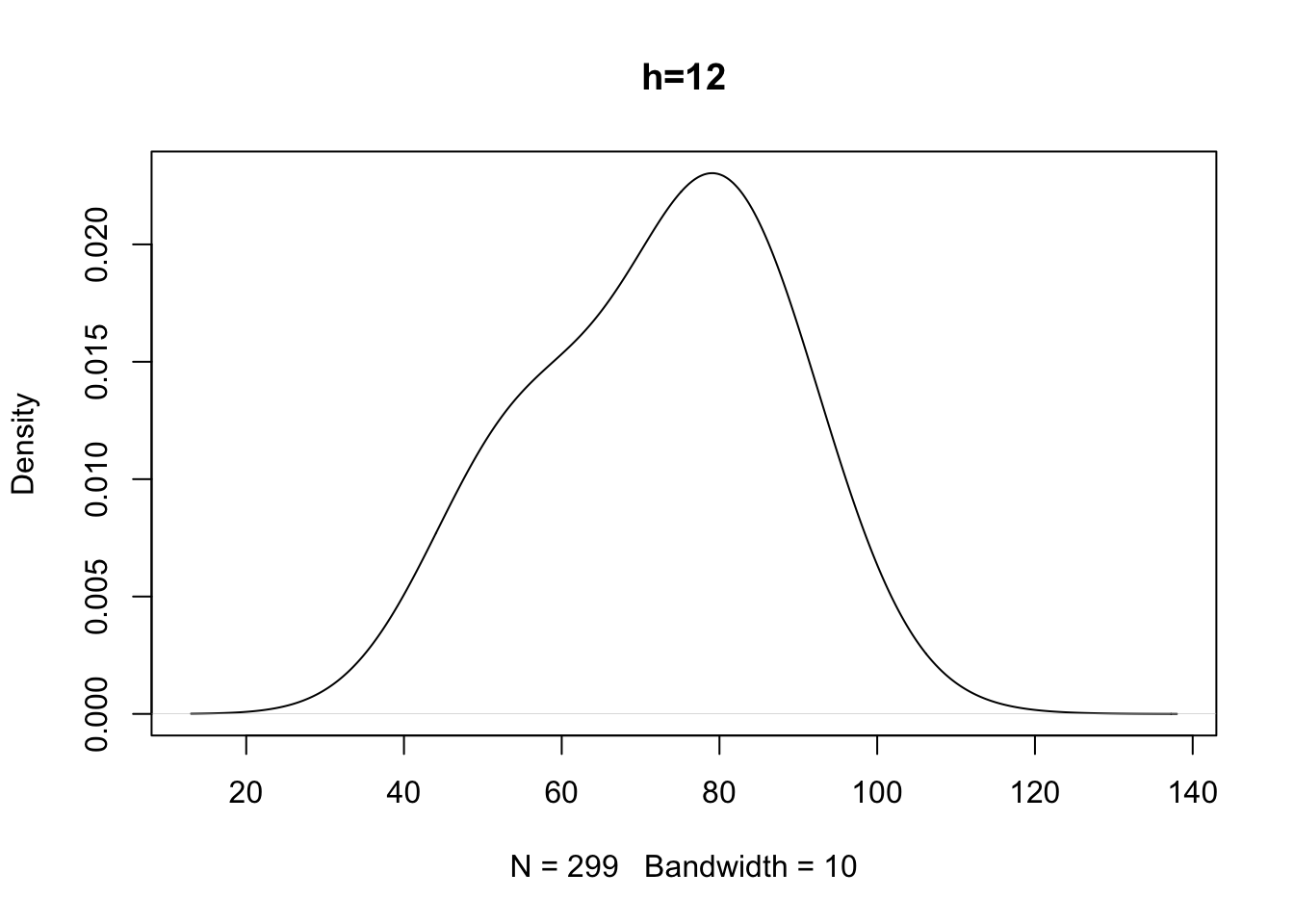
plot(density(geyser$waiting, bw=1), main="h=1")

plot(density(geyser$waiting, bw=4), main="h=4")

plot(density(geyser$waiting, bw=10), main="h=12")

# con un parametro di lisciamento troppo alto si perde la bimodalità
# con uno troppo piccolo appaiono delle  variazioni brusche nella
# densità che riflettono densità locali (è come fare un istogramma
# con troppe classi rispetto alla numerosità dei dati)

Con insiemi di dati che presentano forte asimmetria il valore di $h$ scelto potrebbe essere adeguato per le regioni in cui la densità è alta e essere invece troppo piccolo per ottenere un buon grado di lisciamento lungo la coda. è possibile in tal caso introdurre criteri flessibili che permettano di utilizzare valori di $h$ diversi in relazione alla diversa densità locale dei dati.

In generale, è consigliabile ottenere differenti curve di densità per diversi valori di $h$ e giudicare a posteriori quale valore di $h$ mostri di cogliere adeguatamente le caratteristiche salienti dell’insieme di dati.

Tuttavia è possibile tenere presenti alcuni semplici criteri pratici. è ad esempio ragionevole attendersi che il valore di $h$ ideale sia inversamente proporzionale ad una funzione di $n$. In genere si consiglia di scegliere $h$ proporzionale a $n^{-\frac{1}{5}}$. Se si usa una funzione nucleo gaussiana il valore di $h$ di default è $h=0,9 A n^{-\frac{1}{5}}$ ove \[ A=\frac{min(\mbox{scarto quadratico medio},\mbox{scarto interquartile})}{1.34}. \]

Per le altre opzioni della funzione density si rinvia a quanto contenuto nella documentazione in linea di R. Esiste nella Base di R la funzione ksmooth() che funziona in modo analogo alla density(). Una seconda funzione, anche più generale, per determinare la funzione di densità con il metodo del nucleo è la bkde() nel package KernSmooth.