3 Functions and Loops

3.1 Introduction

In programming, we often perform the same tasks repeatedly. Functions and Loops help us write cleaner, shorter, and more efficient code.

Function is a block of code that can be called anytime to perform a specific task.
Loop is used to run the same code repeatedly without rewriting it.

3.2 What Is a Function?

A function is a block of code designed to perform a specific task. Using functions helps us avoid redundant code.

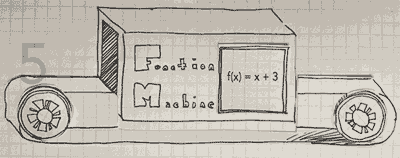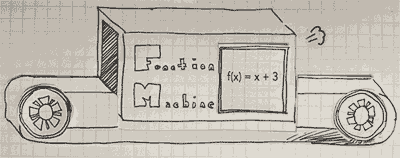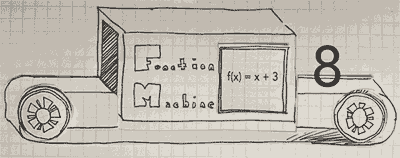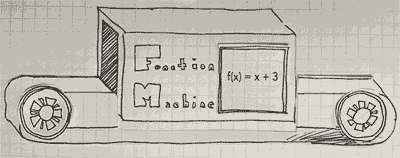
This visual representation helps illustrate how functions work systematically. The label “Function Machine” on the machine reinforces that it applies a specific rule to transform the input into an output. The function in the image is:

\[f(x) = x + 3\]

This means that any number inputted into the machine will have 3 added to it before being output.

3.2.1 Function in $ax+b$

This function takes three numbers as inputs and returns their calculation.

Python Code

# Function to multiply 'a' with 'x' and add 'b'
def function1(a, x, b):
    return a * x + b

# Example usage
print(function1(2, 3, 4))  # Output: (2 * 3) + 4 = 10

R Code

# Function to multiply 'a' with 'x' and add 'b'
function1 <- function(a, x, b) {
  return(a * x + b)
}

# Example usage
print(function1(2, 3, 4))  # Output: (2 * 3) + 4 = 10

[1] 10

3.2.2 Value Comparator

This function analyzes two datasets by calculating their mean, median, and standard deviation, useful in data analysis.

Python Code

import statistics
from tabulate import tabulate

# Function to compare two datasets
def compare_data(group1, group2):
    return {
        "group1": {
            "mean": statistics.mean(group1),
            "median": statistics.median(group1),
            "std_dev": statistics.stdev(group1)
        },
        "group2": {
            "mean": statistics.mean(group2),
            "median": statistics.median(group2),
            "std_dev": statistics.stdev(group2)
        }
    }

# Sample datasets
data1 = [10, 20, 30, 40, 50]
data2 = [15, 25, 35, 45, 55]

# Get results
results = compare_data(data1, data2)

# Convert results to a table format
table = [
    ["Metric", "Group 1", "Group 2"],
    ["Mean", results["group1"]["mean"], results["group2"]["mean"]],
    ["Median", results["group1"]["median"], results["group2"]["median"]],
    ["Standard Deviation", results["group1"]["std_dev"], results["group2"]["std_dev"]]
]

# Print table
print(tabulate(table, headers="firstrow", tablefmt="grid"))

+--------------------+-----------+-----------+
| Metric             |   Group 1 |   Group 2 |
+====================+===========+===========+
| Mean               |   30      |   35      |
+--------------------+-----------+-----------+
| Median             |   30      |   35      |
+--------------------+-----------+-----------+
| Standard Deviation |   15.8114 |   15.8114 |
+--------------------+-----------+-----------+

R Code

# Load library
library(knitr)

# Function to compare two datasets
compare_data <- function(group1, group2) {
  data.frame(
    Statistic = c("Mean", "Median", "Std Dev"),
    Group1 = round(c(mean(group1), median(group1), sd(group1)), 2),
    Group2 = round(c(mean(group2), median(group2), sd(group2)), 2)
  )
}

# Sample data
data1 <- c(10, 20, 30, 40, 50)
data2 <- c(15, 25, 35, 45, 55)

# Print as formatted table
kable(compare_data(data1, data2))

Statistic	Group1	Group2
Mean	30.00	35.00
Median	30.00	35.00
Std Dev	15.81	15.81

Functions save time by allowing code reuse, improve program organization and readability, and make debugging and future development easier.

3.2.3 Geometric Properties

In the field of computational geometry, functions are essential for converting mathematical expressions into executable code. For example, the formulas for calculating the area and perimeter of various two-dimensional shapes can be implemented as separate functions. This approach makes the development process more efficient and easier to manage. The following sections explain in detail how these geometric formulas are coded, using Python and R as examples.

Shape	Area Formula (A)	Perimeter Formula (P)	Variables Description
Triangle	$A = \frac{1}{2}(b \times h)$	$P = a + b + c$	$b$ = base, $h$ = height, $a$, $b$, $c$ = sides
Rectangle	$A = l \times b$	$P = 2(l+b)$	$l$ = length, $b$ = breadth
Square	$A = s \times s$	$P = 4 \times s$	$s$ = side
Circle	$A = \pi r^2$	$P = 2\pi r$	$r$ = radius, $\pi = 3.14$ or $\frac{22}{7}$
Ellipse	$A = \pi \times a \times b$	$P = \pi(a+b)$	$a$ = semi-major axis, $b$ = semi-minor axis
Parallelogram	$A = b \times h$	$P = 2(a+b)$	$b$ = base, $h$ = height, $a$, $b$ = lengths of opposite sides
Rhombus	$A = \frac{1}{2}(d_1 \times d_2)$	$P = 4 \times a$	$d_1, d_2$ = diagonals, $a$ = side
Trapezium	$A = \frac{1}{2}(a+b) \times h$	Sum of all sides	$a$, $b$ = lengths of parallel sides, $h$ = height

With the formulas provided above, you can create functions that calculate the area and perimeter for different shapes. This not only makes your code modular and easier to maintain but also enables you to test individual pieces of logic in isolation. This example below in Python and R that demonstrate how to implement functions for these calculations.

Python Code

import math

# Function to calculate area and perimeter for multiple shapes
def calculate_area_perimeter(shape, **kwargs):
    if shape == "triangle":
        base = kwargs.get("base")
        height = kwargs.get("height")
        side_a = kwargs.get("side_a")
        side_b = kwargs.get("side_b")
        side_c = kwargs.get("side_c")
        area = 0.5 * base * height
        perimeter = side_a + side_b + side_c
    elif shape == "rectangle":
        length = kwargs.get("length")
        breadth = kwargs.get("breadth")
        area = length * breadth
        perimeter = 2 * (length + breadth)
    elif shape == "square":
        side = kwargs.get("side")
        area = side ** 2
        perimeter = 4 * side
    elif shape == "circle":
        radius = kwargs.get("radius")
        area = math.pi * radius ** 2
        perimeter = 2 * math.pi * radius
    elif shape == "ellipse":
        a = kwargs.get("a")
        b = kwargs.get("b")
        area = math.pi * a * b
        perimeter = math.pi * (a + b)
    elif shape == "parallelogram":
        base = kwargs.get("base")
        height = kwargs.get("height")
        side_a = kwargs.get("side_a")
        side_b = kwargs.get("side_b")
        area = base * height
        perimeter = 2 * (side_a + side_b)
    elif shape == "rhombus":
        d1 = kwargs.get("d1")
        d2 = kwargs.get("d2")
        side = kwargs.get("side")
        area = 0.5 * d1 * d2
        perimeter = 4 * side
    elif shape == "trapezium":
        a = kwargs.get("a")
        b = kwargs.get("b")
        height = kwargs.get("height")
        side_a = kwargs.get("side_a")
        side_b = kwargs.get("side_b")
        area = 0.5 * (a + b) * height
        perimeter = a + b + side_a + side_b
    else:
        return "Invalid shape. Choose a valid 2D shape."

    return {"area": area, "perimeter": perimeter}

# Example usage
result = calculate_area_perimeter("triangle", 
                                  base=6, 
                                  height=4, 
                                  side_a=5, 
                                  side_b=6, 
                                  side_c=7)
print("Triangle-Area & Perimeter:", result["area"], "and", result["perimeter"])

Triangle-Area & Perimeter: 12.0 and 18

R Code

# Function to calculate area and perimeter for multiple shapes
calculate_area_perimeter <- function(shape, ...) {
  args <- list(...)
  
  if (shape == "triangle") {
    base <- args$base
    height <- args$height
    side_a <- args$side_a
    side_b <- args$side_b
    side_c <- args$side_c
    area <- 0.5 * base * height
    perimeter <- side_a + side_b + side_c
  } else if (shape == "rectangle") {
    length <- args$length
    breadth <- args$breadth
    area <- length * breadth
    perimeter <- 2 * (length + breadth)
  } else if (shape == "square") {
    side <- args$side
    area <- side^2
    perimeter <- 4 * side
  } else if (shape == "circle") {
    radius <- args$radius
    area <- pi * radius^2
    perimeter <- 2 * pi * radius
  } else if (shape == "ellipse") {
    a <- args$a
    b <- args$b
    area <- pi * a * b
    perimeter <- pi * (a + b)
  } else if (shape == "parallelogram") {
    base <- args$base
    height <- args$height
    side_a <- args$side_a
    side_b <- args$side_b
    area <- base * height
    perimeter <- 2 * (side_a + side_b)
  } else if (shape == "rhombus") {
    d1 <- args$d1
    d2 <- args$d2
    side <- args$side
    area <- 0.5 * d1 * d2
    perimeter <- 4 * side
  } else if (shape == "trapezium") {
    a <- args$a
    b <- args$b
    height <- args$height
    side_a <- args$side_a
    side_b <- args$side_b
    area <- 0.5 * (a + b) * height
    perimeter <- a + b + side_a + side_b
  } else {
    stop("Invalid shape. Choose a valid 2D shape.")
  }
  
  return(list(area = area, perimeter = perimeter))
}

# Example usage
result <- calculate_area_perimeter("triangle", 
                                   base = 6, 
                                   height = 4, 
                                   side_a = 5, 
                                   side_b = 6, 
                                   side_c = 7)
cat("Triangle - Area & Perimeter:", result$area, "and", result$perimeter, "\n")

Triangle - Area & Perimeter: 12 and 18

3.3 What Is a Loop?

Loops allow us to execute the same code multiple times without rewriting it. Loops allow us to perform repetitive calculations for mathematical analysis and data processing. Types of Loops:

For Loop – Used when the number of repetitions is known.
While Loop – Used when repetitions depend on a condition.

3.3.1 Fibonacci Sequence

The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones:

\[F(n) = F(n-1) + F(n-2)\]

Example: $0,1,1,2,3,5,8,13,21,\dots$

Python Code

def fibonacci(n):
    fib_series = [0, 1]
    for i in range(2, n):
        fib_series.append(fib_series[-1] + fib_series[-2])
    return fib_series

print(fibonacci(10))  # Output: [0, 1, 1, 2, 3, 5, 8, 13, 21, 34]

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]

3.3.1.1 R Code

fibonacci <- function(n) {
  fib_series <- c(0, 1)
  for (i in 3:n) {
    fib_series <- c(fib_series, fib_series[i-1] + fib_series[i-2])
  }
  return(fib_series)
}

print(fibonacci(10))  # Output: 0 1 1 2 3 5 8 13 21 34

 [1]  0  1  1  2  3  5  8 13 21 34

3.3.2 Arithmetic & Geometric Sequences

This function generates a sequence based on the type specified: either an arithmetic sequence or a geometric sequence. For an arithmetic sequence, each term is obtained by adding a constant difference to the previous term. For a geometric sequence, each term is obtained by multiplying the previous term by a constant ratio.

Python Code

def generate_sequence(seq_type, n, a, d=None, r=None):
    """
    Generate an arithmetic or geometric sequence.

    Parameters:
        seq_type (str): Type of sequence - "arithmetic" or "geometric".
        n (int): The number of terms in the sequence.
        a (numeric): The first term of the sequence.
        d (numeric, optional): The common difference (required for arithmetic).
        r (numeric, optional): The common ratio (required for geometric).

    Returns:
        list: A list containing the generated sequence.
    """
    sequence = []
    if seq_type.lower() == "arithmetic":
        if d is None:
            raise ValueError("'d' must be provided for an arithmetic sequence")
        for i in range(n):
            sequence.append(a + i * d)
    elif seq_type.lower() == "geometric":
        if r is None:
            raise ValueError("'r' must be provided for a geometric sequence")
        for i in range(n):
            sequence.append(a * (r ** i))
    else:
        raise ValueError("seq_type must be either 'arithmetic' or 'geometric'")
    return sequence

# Example usage:
print(generate_sequence("arithmetic", 10, 1, d=2))

[1, 3, 5, 7, 9, 11, 13, 15, 17, 19]

print(generate_sequence("geometric", 10, 1, r=3))

[1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683]

R Code

generate_sequence <- function(seq_type, n, a, d = NULL, r = NULL) {
  #' Generate an arithmetic or geometric sequence.
  #'
  #' @param seq_type specifying the type of sequence:"arithmetic"/"geometric".
  #' @param n The number of terms in the sequence.
  #' @param a The first term of the sequence.
  #' @param d The common difference (required for arithmetic sequences).
  #' @param r The common ratio (required for geometric sequences).
  #'
  #' @return A numeric vector containing the generated sequence.
  
  sequence <- numeric(n)
  if (tolower(seq_type) == "arithmetic") {
    if (is.null(d)) stop("'d' must be provided for an arithmetic sequence.")
    for (i in 1:n) {
      sequence[i] <- a + (i - 1) * d
    }
  } else if (tolower(seq_type) == "geometric") {
    if (is.null(r)) stop("'r' must be provided for a geometric sequence.")
    for (i in 1:n) {
      sequence[i] <- a * (r^(i - 1))
    }
  } else {
    stop("seq_type must be either 'arithmetic' or 'geometric'")
  }
  return(sequence)
}

# Example usage:
print(generate_sequence("arithmetic", 10, 1, d = 2))

 [1]  1  3  5  7  9 11 13 15 17 19

print(generate_sequence("geometric", 10, 1, r = 3))

 [1]     1     3     9    27    81   243   729  2187  6561 19683

3.3.3 Simple Linear Regression

Linear regression is used to find the relationship between an independent variable $X$ and a dependent variable $Y$:

\[Y = aX + b\]

where:

$a$ is the slope
$b$ is the intercept

Python Code

import numpy as np

# Data (X: study hours, Y: exam scores)
X = np.array([1, 2, 3, 4, 5])
Y = np.array([2, 4, 5, 4, 5])

# Calculate slope (a) and intercept (b)
n = len(X)
sum_x, sum_y = sum(X), sum(Y)
sum_xy = sum(X * Y)
sum_x2 = sum(X ** 2)

a = (n * sum_xy - sum_x * sum_y) / (n * sum_x2 - sum_x ** 2)
b = (sum_y - a * sum_x) / n

print(f"Linear Regression: Y = {a:.2f}X + {b:.2f}")

Linear Regression: Y = 0.60X + 2.20

R Code

# Data
X <- c(1, 2, 3, 4, 5)
Y <- c(2, 4, 5, 4, 5)

# Calculate slope (a) and intercept (b)
n <- length(X)
sum_x <- sum(X)
sum_y <- sum(Y)
sum_xy <- sum(X * Y)
sum_x2 <- sum(X^2)

a <- (n * sum_xy - sum_x * sum_y) / (n * sum_x2 - sum_x^2)
b <- (sum_y - a * sum_x) / n

print(paste("Linear Regression: Y =", round(a, 2), "X +", round(b, 2)))

[1] "Linear Regression: Y = 0.6 X + 2.2"

Functions and loops help us create simpler and more efficient code. By understanding these two concepts, we can write better and more readable programs.

3.4 Applied of Functions and Loops

Let’s apply these Functions and Loops to real-world data science tasks:

3.4.1 Creating a Dataset

Python Code

import pandas as pd
import random

def create_employee_dataset(num_employees):
    positions = {
        "Staff": (3000, 5000, 1, 5),
        "Supervisor": (5000, 8000, 5, 10),
        "Manager": (8000, 12000, 10, 15),
        "Director": (12000, 15000, 15, 25)
    }
    
    departments = ["Finance", "HR", "IT", "Marketing", "Operations", "Sales"]
    locations = ["New York", "Los Angeles", "Chicago", "Houston", "Phoenix"]
    
    data = {
        "ID_Number": [],
        "Position": [],
        "Salary": [],
        "Age": [],
        "Experience": [],
        "Department": [],
        "Location": []
    }
    
    for _ in range(num_employees):
        id_number = random.randint(10000, 99999)
        position = random.choice(list(positions.keys()))
        salary = random.randint(positions[position][0], 
                 positions[position][1])
        experience = random.randint(positions[position][2], 
                      positions[position][3])
        age = experience + random.randint(22, 35)  # aligns with experience
        department = random.choice(departments)
        location = random.choice(locations)
        
        data["ID_Number"].append(id_number)
        data["Position"].append(position)
        data["Salary"].append(salary)
        data["Age"].append(age)
        data["Experience"].append(experience)
        data["Department"].append(department)
        data["Location"].append(location)
    
    return pd.DataFrame(data)

# Create the employee dataset
df = create_employee_dataset(20)
print(df)

    ID_Number    Position  Salary  Age  Experience  Department     Location
0       81341     Manager   11352   47          13       Sales     New York
1       52591  Supervisor    5466   29           5       Sales  Los Angeles
2       71794       Staff    4201   40           5       Sales      Chicago
3       35098     Manager   11046   44          14          IT      Phoenix
4       44337       Staff    4638   31           4     Finance      Houston
5       40107     Manager   10637   47          12  Operations      Chicago
6       21790  Supervisor    5746   36           7          IT      Phoenix
7       17060  Supervisor    6078   33           6          IT      Phoenix
8       67971       Staff    4672   31           5       Sales      Houston
9       44172     Manager   11605   34          12     Finance     New York
10      40220  Supervisor    6328   32           7       Sales      Houston
11      60793  Supervisor    7153   28           5       Sales  Los Angeles
12      30595  Supervisor    5051   30           8          IT      Phoenix
13      45161  Supervisor    6827   39           6   Marketing  Los Angeles
14      42268  Supervisor    6556   39           6       Sales  Los Angeles
15      74667  Supervisor    7727   31           9     Finance      Houston
16      94126       Staff    4255   30           2  Operations  Los Angeles
17      81800       Staff    3543   37           2       Sales      Phoenix
18      73586  Supervisor    7297   35           8  Operations      Houston
19      17845    Director   14764   52          22   Marketing  Los Angeles

R Code

create_employee_dataset <- function(num_employees) {
  # Define positions with corresponding salary and experience ranges
  positions <- list(
    "Staff" = c(3000, 5000, 1, 5),
    "Supervisor" = c(5000, 8000, 5, 10),
    "Manager" = c(8000, 12000, 10, 15),
    "Director" = c(12000, 15000, 15, 25)
  )
  
  # Define additional categorical data: departments and locations
  departments <- c("Finance", "HR", "IT", "Marketing", "Operations", "Sales")
  locations <- c("New York", "Los Angeles", "Chicago", "Houston", "Phoenix")
  
  # Initialize empty vectors for each column
  ID_Number <- integer(num_employees)
  Position <- character(num_employees)
  Salary <- integer(num_employees)
  Age <- integer(num_employees)
  Experience <- integer(num_employees)
  Department <- character(num_employees)
  Location <- character(num_employees)
  
  # Generate data for each employee
  for (i in 1:num_employees) {
    ID_Number[i] <- sample(10000:99999, 1)
    pos <- sample(names(positions), 1)
    Position[i] <- pos
    
    salary_range <- positions[[pos]][1:2]
    Salary[i] <- sample(salary_range[1]:salary_range[2], 1)
    
    exp_range <- positions[[pos]][3:4]
    Experience[i] <- sample(exp_range[1]:exp_range[2], 1)
    
    Age[i] <- Experience[i] + sample(22:35, 1)
    Department[i] <- sample(departments, 1)
    Location[i] <- sample(locations, 1)
  }
  
  # Combine the vectors into a data frame
  df <- data.frame(
    ID_Number = ID_Number,
    Position = Position,
    Salary = Salary,
    Age = Age,
    Experience = Experience,
    Department = Department,
    Location = Location,
    stringsAsFactors = FALSE
  )
  
  return(df)
}

# Example usage:
df <- create_employee_dataset(20)
print(df)

   ID_Number   Position Salary Age Experience Department    Location
1      69234   Director  12640  49         22 Operations     Houston
2      80527    Manager   9701  44         10    Finance     Phoenix
3      97411 Supervisor   7418  43          8  Marketing     Phoenix
4      27080   Director  12855  47         17      Sales     Chicago
5      33747    Manager   9984  32         10    Finance    New York
6      61960      Staff   4807  27          1  Marketing    New York
7      10731    Manager  11119  40         11         HR    New York
8      63971 Supervisor   5794  41          6  Marketing     Houston
9      44077    Manager  11335  38         12  Marketing    New York
10     39831   Director  14628  48         18 Operations     Houston
11     16524      Staff   4641  31          5 Operations    New York
12     66562    Manager   8777  46         14         IT Los Angeles
13     42653 Supervisor   7694  44         10    Finance     Chicago
14     11767      Staff   3000  39          5         HR     Chicago
15     95766   Director  14270  47         24  Marketing    New York
16     48978      Staff   3196  38          5    Finance     Chicago
17     92076      Staff   3872  39          4      Sales     Chicago
18     67811      Staff   3064  29          3    Finance     Chicago
19     31942   Director  13987  43         17    Finance     Phoenix
20     22611 Supervisor   5493  33          9    Finance Los Angeles

3.4.2 Basic Statistics

Python Code

import pandas as pd
import numpy as np

def manual_statistics(df, column=None):
    def stats_for_column(values):
        # Remove missing values for accurate computations
        values = values.dropna()
        if pd.api.types.is_numeric_dtype(values):
            count = len(values)
            mean_value = np.mean(values)
            median_value = np.median(values)
            variance_value = np.var(values, ddof=1) if count > 1 else 0
            std_dev_value = np.sqrt(variance_value)
            min_value = np.min(values)
            max_value = np.max(values)
            q1 = np.percentile(values, 25)
            q3 = np.percentile(values, 75)
            return {
                "count": count,
                "mean": mean_value,
                "median": median_value,
                "variance": variance_value,
                "std_dev": std_dev_value,
                "min": min_value,
                "q1": q1,
                "q3": q3,
                "max": max_value
            }
        else:
            count = len(values)
            unique_count = values.nunique()
            mode_series = values.mode()
            mode_value = mode_series.iloc[0] if not mode_series.empty else None
            frequency = values.value_counts().to_dict()
            return {
                "count": count,
                "unique": unique_count,
                "mode": mode_value,
                "frequency": frequency
            }

    if column is not None:
        return stats_for_column(df[column])
    else:
        summary = {}
        for col in df.columns:
            summary[col] = stats_for_column(df[col])
        return summary

# Get summary statistics for all columns
stats_all = manual_statistics(df)

# Display the results in attractive tables using pandas' to_markdown()
for col, stats in stats_all.items():
    print(f"\n### Summary Statistics for '{col}'\n")
    if pd.api.types.is_numeric_dtype(df[col]):
        # Create a DataFrame for numeric statistics with Statistic and Value 
        stats_df = pd.DataFrame({
            "Statistic": list(stats.keys()),
            "Value": list(stats.values())
        })
        print(stats_df.to_markdown(index=False))
    else:
        # For categorical data, create summary table and frequency distribution
        summary_df = pd.DataFrame({
            "Statistic": ["count", "unique", "mode"],
            "Value": [stats["count"], stats["unique"], stats["mode"]]
        })
        freq_dict = stats["frequency"]
        freq_df = pd.DataFrame({
            "Category": list(freq_dict.keys()),
            "Frequency": list(freq_dict.values())
        })
        print(summary_df.to_markdown(index=False))
        print("\n")
        print(freq_df.to_markdown(index=False))


### Summary Statistics for 'ID_Number'

| Statistic   |           Value |
|:------------|----------------:|
| count       |    20           |
| mean        | 51866.1         |
| median      | 44749           |
| variance    |     5.16475e+08 |
| std_dev     | 22726.1         |
| min         | 17060           |
| q1          | 38854.8         |
| q3          | 72242           |
| max         | 94126           |

### Summary Statistics for 'Position'

| Statistic   | Value      |
|:------------|:-----------|
| count       | 20         |
| unique      | 4          |
| mode        | Supervisor |


| Category   |   Frequency |
|:-----------|------------:|
| Supervisor |          10 |
| Staff      |           5 |
| Manager    |           4 |
| Director   |           1 |

### Summary Statistics for 'Salary'

| Statistic   |           Value |
|:------------|----------------:|
| count       |    20           |
| mean        |  7247.1         |
| median      |  6442           |
| variance    |     9.31655e+06 |
| std_dev     |  3052.3         |
| min         |  3543           |
| q1          |  4956.25        |
| q3          |  8454.5         |
| max         | 14764           |

### Summary Statistics for 'Age'

| Statistic   |    Value |
|:------------|---------:|
| count       | 20       |
| mean        | 36.25    |
| median      | 34.5     |
| variance    | 46.6184  |
| std_dev     |  6.82777 |
| min         | 28       |
| q1          | 31       |
| q3          | 39.25    |
| max         | 52       |

### Summary Statistics for 'Experience'

| Statistic   |    Value |
|:------------|---------:|
| count       | 20       |
| mean        |  7.9     |
| median      |  6.5     |
| variance    | 22.5158  |
| std_dev     |  4.74508 |
| min         |  2       |
| q1          |  5       |
| q3          |  9.75    |
| max         | 22       |

### Summary Statistics for 'Department'

| Statistic   | Value   |
|:------------|:--------|
| count       | 20      |
| unique      | 5       |
| mode        | Sales   |


| Category   |   Frequency |
|:-----------|------------:|
| Sales      |           8 |
| IT         |           4 |
| Finance    |           3 |
| Operations |           3 |
| Marketing  |           2 |

### Summary Statistics for 'Location'

| Statistic   | Value       |
|:------------|:------------|
| count       | 20          |
| unique      | 5           |
| mode        | Los Angeles |


| Category    |   Frequency |
|:------------|------------:|
| Los Angeles |           6 |
| Phoenix     |           5 |
| Houston     |           5 |
| New York    |           2 |
| Chicago     |           2 |

R code

library(knitr)
library(kableExtra)

manual_statistics <- function(df, column = NULL) {
  # Helper function to compute statistics for a single column
  stats_for_column <- function(values) {
    # Remove NA values for accurate computations
    values <- values[!is.na(values)]
    
    if (is.numeric(values)) {
      count <- length(values)
      mean_value <- mean(values)
      median_value <- median(values)
      variance_value <- if (count > 1) var(values) else 0
      std_dev_value <- sqrt(variance_value)
      min_value <- min(values)
      max_value <- max(values)
      q1 <- as.numeric(quantile(values, 0.25))
      q3 <- as.numeric(quantile(values, 0.75))
      
      return(list(
        count    = count,
        mean     = mean_value,
        median   = median_value,
        variance = variance_value,
        std_dev  = std_dev_value,
        min      = min_value,
        q1       = q1,
        q3       = q3,
        max      = max_value
      ))
    } else {
      count <- length(values)
      unique_count <- length(unique(values))
      tab <- table(values)
      mode_value <- names(tab)[which.max(tab)]
      frequency <- as.list(tab)
      
      return(list(
        count     = count,
        unique    = unique_count,
        mode      = mode_value,
        frequency = frequency
      ))
    }
  }
  
  # If a specific column is provided, compute statistics only for that column.
  if (!is.null(column)) {
    return(stats_for_column(df[[column]]))
  } else {
    # Otherwise, compute statistics for each column in the DataFrame.
    summary <- list()
    for (col in names(df)) {
      summary[[col]] <- stats_for_column(df[[col]])
    }
    return(summary)
  }
}

# Hitung summary statistics untuk semua kolom
stats_all <- manual_statistics(df)

# Loop untuk menampilkan hasil setiap kolom dengan DT::datatable
for (col in names(stats_all)) {
  cat(paste0("<h3>Summary Statistics for '", col, "'</h3>"))
  
  col_stats <- stats_all[[col]]
  
  if (is.numeric(df[[col]])) {
    stats_df <- data.frame(
      Statistic = names(col_stats),
      Value = as.numeric(unlist(col_stats)),
      stringsAsFactors = FALSE
    )
    print(DT::datatable(stats_df, 
                        caption = paste("Summary for", col),
                        options = list(pageLength = 5, autoWidth = TRUE)))
  } else {
    summary_df <- data.frame(
      Statistic = c("count", "unique", "mode"),
      Value = c(col_stats$count, col_stats$unique, col_stats$mode),
      stringsAsFactors = FALSE
    )
    freq_df <- as.data.frame(do.call(rbind, col_stats$frequency))
    freq_df <- cbind(Category = rownames(freq_df), freq_df)
    rownames(freq_df) <- NULL
    names(freq_df)[2] <- "Frequency"
    
    print(DT::datatable(summary_df, 
                        caption = paste("Summary for", col),
                        options = list(pageLength = 5, autoWidth = TRUE)))
    cat("<br>")
    print(DT::datatable(freq_df, 
                        caption = paste("Frequency Distribution for", col),
                        options = list(pageLength = 5, autoWidth = TRUE)))
  }
  
  cat("<br><br>")
}

FALSE <h3>Summary Statistics for 'ID_Number'</h3><br><br><h3>Summary Statistics for 'Position'</h3><br><br><br><h3>Summary Statistics for 'Salary'</h3><br><br><h3>Summary Statistics for 'Age'</h3><br><br><h3>Summary Statistics for 'Experience'</h3><br><br><h3>Summary Statistics for 'Department'</h3><br><br><br><h3>Summary Statistics for 'Location'</h3><br><br><br>

Shape	Area Formula (A)	Perimeter Formula (P)	Variables Description
Triangle	\(A = \frac{1}{2}(b \times h)\)	\(P = a + b + c\)	\(b\) = base, \(h\) = height, \(a\), \(b\), \(c\) = sides
Rectangle	\(A = l \times b\)	\(P = 2(l+b)\)	\(l\) = length, \(b\) = breadth
Square	\(A = s \times s\)	\(P = 4 \times s\)	\(s\) = side
Circle	\(A = \pi r^2\)	\(P = 2\pi r\)	\(r\) = radius, \(\pi = 3.14\) or \(\frac{22}{7}\)
Ellipse	\(A = \pi \times a \times b\)	\(P = \pi(a+b)\)	\(a\) = semi-major axis, \(b\) = semi-minor axis
Parallelogram	\(A = b \times h\)	\(P = 2(a+b)\)	\(b\) = base, \(h\) = height, \(a\), \(b\) = lengths of opposite sides
Rhombus	\(A = \frac{1}{2}(d_1 \times d_2)\)	\(P = 4 \times a\)	\(d_1, d_2\) = diagonals, \(a\) = side
Trapezium	\(A = \frac{1}{2}(a+b) \times h\)	Sum of all sides	\(a\), \(b\) = lengths of parallel sides, \(h\) = height

3.1 Introduction

3.2 What Is a Function?

3.2.1 Function in \(ax+b\)

Python Code

R Code

3.2.2 Value Comparator

Python Code

R Code

3.2.3 Geometric Properties

Python Code

R Code

3.3 What Is a Loop?

3.3.1 Fibonacci Sequence

Python Code

3.3.1.1 R Code

3.3.2 Arithmetic & Geometric Sequences

Python Code

R Code

3.3.3 Simple Linear Regression

Python Code

R Code

3.4 Applied of Functions and Loops

3.4.1 Creating a Dataset

Python Code

R Code

3.4.2 Basic Statistics

Python Code

R code