4 การประยุกต์อินทิกรัลในทางเศรษฐศาสตร์
ในบทนี้ผู้อ่านจะได้เรียนรู้การประยุกต์ใช้การคำนวณเชิงสัญลักษณ์ เพื่อแก้ปัญหาที่เกี่ยวข้องกับการอินทิกรัลในทางเศรษฐศาสตร์ ก่อนผู้อ่านศึกษาเนื้อหาบทนี้ ผู้เขียนมีสมมุติฐานว่าผู้อ่านมีความรู้และความเข้าใจเกี่ยวกับการอินทิกรัลมาบ้างแล้ว
4.1 นิยามของอินทิกรัล (Definition of Integral)
อินทิกรัลคือ ผลรวมของปริมาณเล็ก ๆ (“ผลรวมจำกัด” หรือ limit of sums)
เมื่อเราแบ่งช่วงออกเป็นชิ้นเล็ก ๆ มาก ๆ แล้วเอาพื้นที่ของแต่ละชิ้นมาบวกกัน
4.2 ทฤษฎีบทมูลฐานของแคลคูลัส (Fundamental Theorem of Calculus)
คือทฤษฏีแสดงความเกี่ยวข้องกันระหว่างอนุพันธ์และอินทิกรัล โดยมี 2 ส่วนที่สำคัญคือ
4.3 การหาอินทิกรัลด้วย caracas ใน R
- ติดตั้งและโหลดแพ็กเกจ
library(caracas)- กำหนดตัวแปรสัญลักษณ์ (symbolic variables)
x <- symbol("x")
y <- symbol("y")
t <- symbol("t")(เราต้องสร้างตัวแปรก่อน เช่น \(x\), \(y\)ือ \(s\))
- สร้างฟังก์ชันที่ต้องการอินทิเกรต
ตัวอย่าง
f <- sin(x) # f(x) = sin(x)
g <- exp(-x)
h <- t^3 + t^2 + 4- ใช้คำสั่ง
int()จาก caracas สำหรับการอินทิกรัลไม่จำกัดเขต
int(f, x)\[- \cos{\left(x \right)}\]
fคือฟังก์ชันที่ต้องการอินทิเกรตxคือ ตัวแปรตามที่อินทิเกรต
int(g, x)\[- e^{- x}\]
int(h, t)\[\frac{t^{4}}{4} + \frac{t^{3}}{3} + 4 t\]
การอินทิกรัลไม่จำกัดเขต โดยปกติจะบวกค่าคงที่เข้าไปด้วย แต่การอินทิกรัลโดย caracas จะไม่มีการใส่ค่าคงที่
สำหรับการอินทิกรัลจำกัดเขตด้วย caracas ก็ยังใช้คำสั่ง int() เช่นแต่ต้องคำสั่งถายในไปอีก 2 ตัว คือ - lower ค่าที่ใส่ได้ คือ ตัวเลข ตัวแปรจาก caracas และค่าลบอนันต์ (\(-\infty\) ในอาร์ใช้ -Inf
upperค่าที่ใส่ได้ คือ ตัวเลข ตัวแปรจาก caracas และค่าอนันต์ (\(\infty\) ในอาร์ใช้Inf
ตัวอย่างเช่น
แนะนำให้ให้วาดกราฟก่อนทำการหาค่า อินกรัลจำกัดเขต
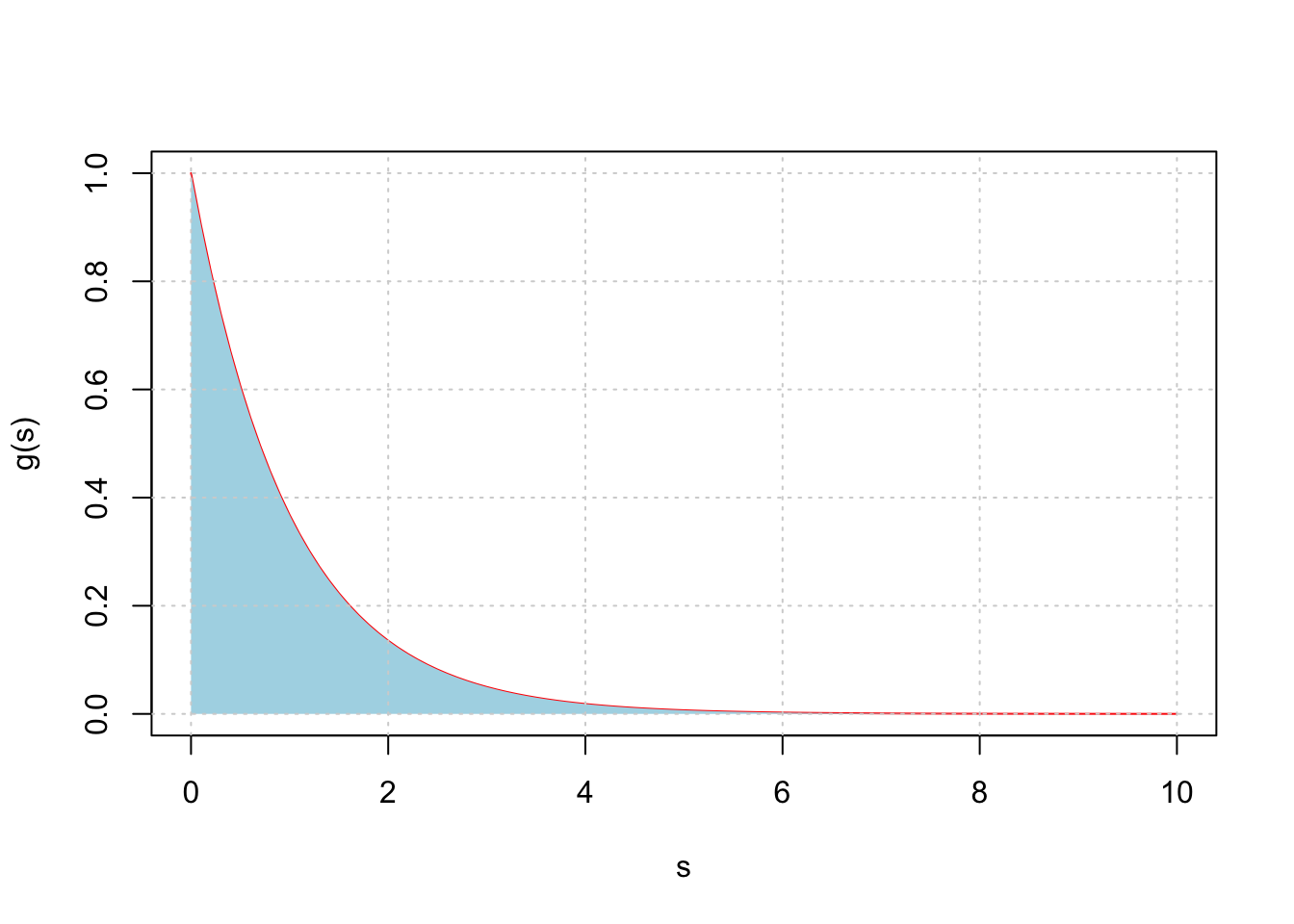
\[\int_{\text{lower}}^{\text{upper}}e^{-s}ds\]
# เปลี่ยนตัวแปร caracas เป็นฟังก์ชันด้วยคำสั่ง as_func()
gs <- as_func(g)
# วาดกราฟด้วยฟังก์ชัน curve เลือกช่วงที่ต้องการ
curve(gs, from = 0, to = 10, col = "red", ylab = "g(s)", xlab = "s")
# สร้างจุดสำหรับวาดพื้นใต้กราฟ
s <- seq(0, 10, length.out = 500)
y <- gs(s)
# แรเงาพื้นที่ใต้เส้น
polygon(c(s, rev(s)), c(rep(0, length(s)), rev(y)),
col = "lightblue", border = NA)
grid()\[\int_{0}^{\infty}e^{-x}dx=1\]
int(g, x, lower = 0, upper = Inf)\[1\]
\[\int_{0}^{t/2}e^{-x}dx=1-e^{- t/2}\]
int(g, x, lower = 0, upper = t/2)\[1 - e^{- \frac{t}{2}}\]
\[\int_{t/2}^{\infty}e^{x}dx=e^{-t/2}\]
int(g, x, lower = t/2, upper = Inf)\[e^{- \frac{t}{2}}\]
4.4 ตัวอย่างการประยุกต์ใช้อินทิกรัลในทางเศรษฐศาสตร์
การคำนวณเชิงสัญลักษณ์ด้วย caracas
# สร้างตัวแปร q
q <- symbol("q")
# สร้างฟังก์ชัน MR(q)
MR <- 100 - 2*q
MR\[100 - 2 q\]
ทำการอินทิกรัลด้วย inv()
TR <- int(MR,q)
TR\[- q^{2} + 100 q\]
อย่าลืม การอินทิกรัลใน caracas จะไม่มีการบวกค่าคงที่
แก้สมการหาค่า \(Q*\) ด้วย caracas แม้ว่าจะเป็นสมการง่ายๆ ก็ตาม
# สร้างตัวแปร Q
Q <- symbol("Q")
# ที่ P = 60 จะได้
f <- 60-120+2*Q
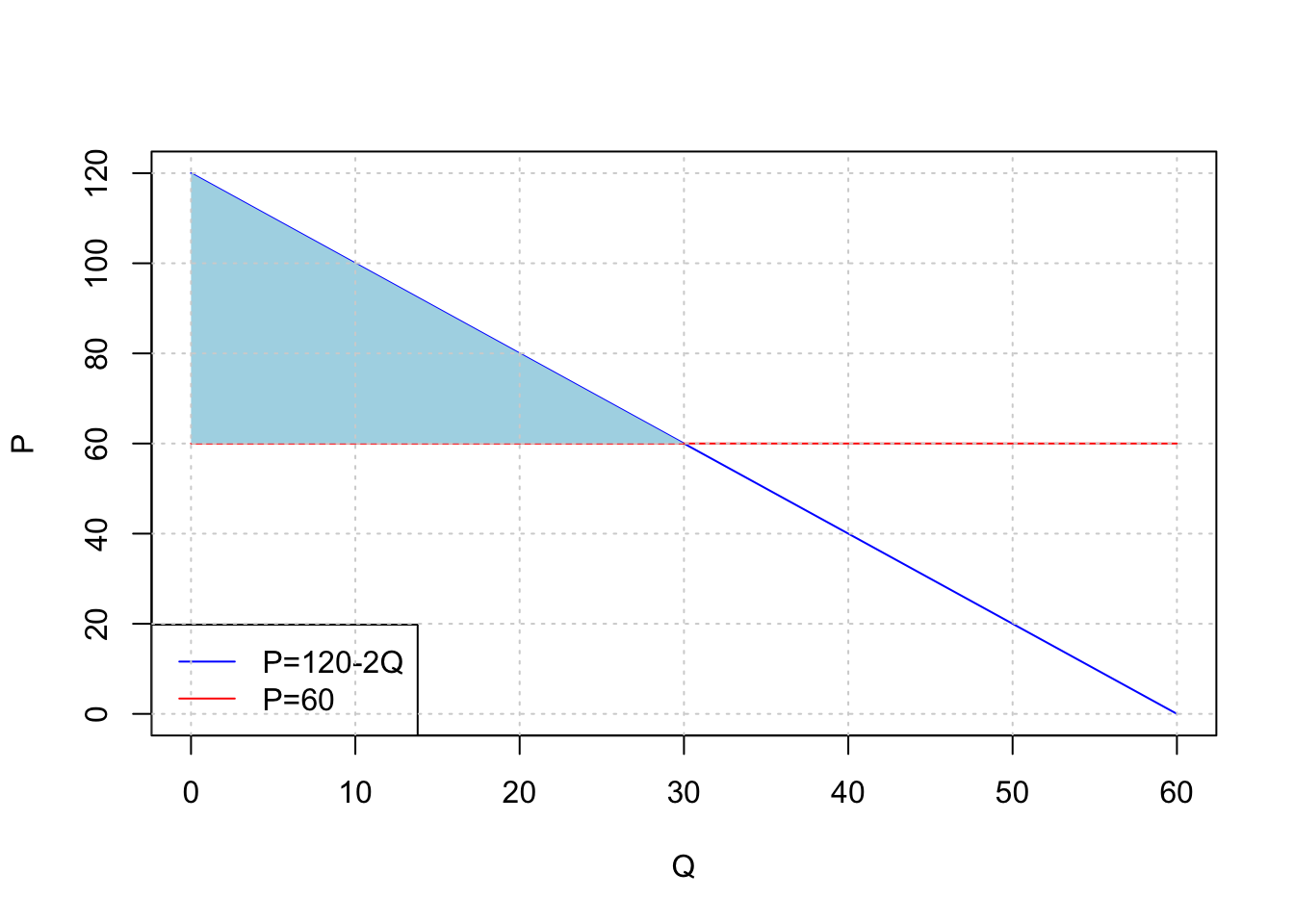
solve_sys(f,Q)Q = 30ดังนั้น ที่ \(P=60\) จะได้ \(Q*=30\) ดังนั้น การอินทิกรัลด้วย caracas จะได้
วาดกราฟเพื่อดูการอินทิกรัล
Pq <- as_func(120-2*Q)
#วาดกราฟ P =120-2Q
curve(Pq, from = 0, to =60, ylab ="P", xlab ="Q", col = "blue")
#เพิ่มกราฟ P = 60
curve(60+0*x,from = 0, to = 60, col = "red", add =TRUE)
# สร้างจุดสำหรับวาดพื้นใต้กราฟ
s <- seq(0, 30, length.out = 500)
y <- Pq(s)
# แรเงาพื้นที่ใต้เส้น
polygon(c(s, rev(s)), c(rep(60, length(s)), rev(y)),
col = "lightblue", border = NA)
legend("bottomleft",c("P=120-2Q","P=60"), col= c("blue","red"), lty =1)
grid()ทำการหาพื้นที่ใต้กราฟ
# สร้างตัวแปร q
q <- symbol("q")
f <- (120-2*q)-60
int(f,q,0,30)\[900\]
จะได้ค่า consumer surplus เท่ากับ 900
การคำนวณเชิงสัญลักษณ์ด้วย caracas
# สร้างตัวแปร t, C และ r
t <- symbol("t")
r <- symbol("r")
C <- 100*exp(0.05*t)
PV <- C/(1+r)^t
PV\[100 \left(r + 1\right)^{- t} e^{0.05 t}\]
แทนค่า \(r=0.08\) ลงไปฟังก์ชัน PV
PV <- subs(PV, r, 0.08)\[100 {1.08}^{- t} e^{0.05 t}\]
วาดกราฟ
PVx <- as_func(PV)
#วาดกราฟ P =120-2Q
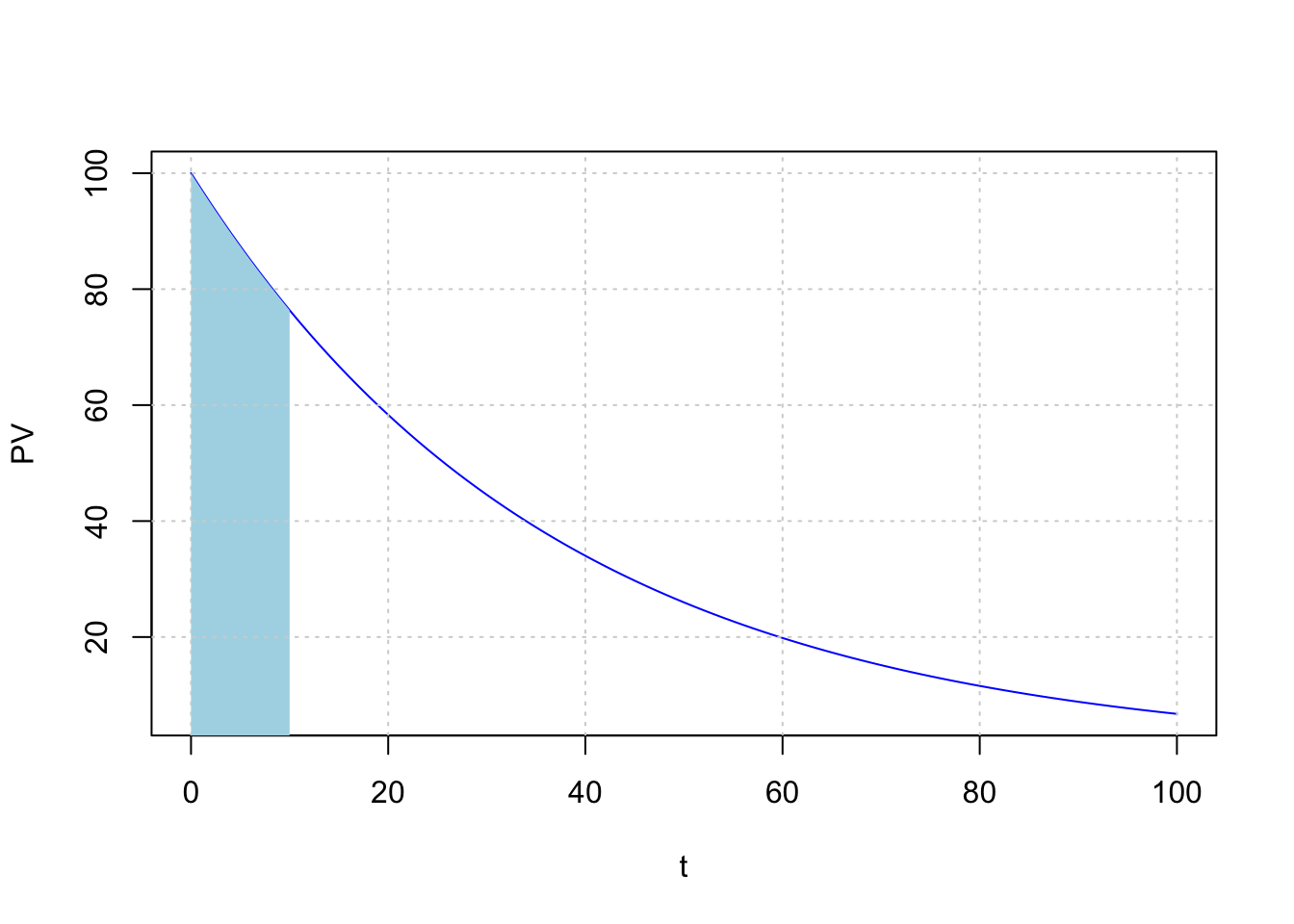
curve(PVx, from = 0, to =100, ylab ="PV", xlab ="t", col = "blue")
s <- seq(0, 10, length.out = 500)
y <- PVx(s)
# แรเงาพื้นที่ใต้เส้น
polygon(c(s, rev(s)), c(rep(0, length(s)), rev(y)),
col = "lightblue", border = NA)
grid()หมายเหตุ เลือกวาดกราฟ ให้ \(t\) มีขนาดยาวเพื่อให้เห็นเส้นโค้งชัดเจน
แสดงสมการอินทิกรัล
int(PV,t, lower = 0, upper = 10, doit = FALSE)\[\int\limits_{0}^{10} 100 {1.08}^{- t} e^{0.05 t}\, dt\]
หาค่า NPV
int(PV,t, lower = 0, upper = 10)\[876.535303483947\]
อินทิกรัลเชิงสัญลักษณ์ด้วยการไม่ใส่ตัวเลขใดๆ จะได้
mu <- symbol("mu")
sigma <- symbol("sigma")
pi <-symbol("pi")
x <- symbol("x")
f <- (1/(sigma*sqrt(2*pi))) * exp(-((x - mu)^2) / (2*sigma^2))
f\[\frac{\sqrt{2} e^{- \frac{\left(- \mu + x\right)^{2}}{2 \sigma^{2}}}}{2 \sqrt{\pi} \sigma}\]
int(f,x, lower = mu, upper = Inf)\[\frac{\sqrt{2} e^{- \frac{\mu^{2}}{2 \sigma^{2}}} \int\limits_{\mu}^{\infty} e^{- \frac{x^{2}}{2 \sigma^{2}}} e^{\frac{\mu x}{\sigma^{2}}}\, dx}{2 \sqrt{\pi} \sigma}\]
เมื่อทดลองแทนค่า \(\mu =0.1\) \(\sigma =0.05\) และ \(\pi\) = pi
f <- subs(f, list(mu = 0.01, sigma =0.05))
f\[\frac{10.0 \sqrt{2} e^{- 200.0 \left(x - 0.01\right)^{2}}}{\sqrt{\pi}}\]
เนื่องจากภาษาอาร์ pi คือตัวแปรของค่าคงของค่าพาย แต่เนื่องจากมีกำหนดให้ pi คือแปรใหม่ที่สร้างจาก caracas ดังนั้นต้องดึงค่าคงพายจากชุดคำสั่ง base มาใช้ด้วยคำสั่ง base::pi <ชุดคำสั่ง::ฟังก์ชัน/ค่าคงที่ที่ต้องการใช้>
ทำการอินทิกรัลจะได้
int(f,x, lower = 0.01, upper = Inf)\[\frac{0.353553390593274 \sqrt{2} \sqrt{\pi}}{\sqrt{\pi}}\]
ถ์้าต้องการเป็นตัวเลขจะได้
N(subs(int(f,x, lower = 0.01, upper = Inf), pi, base::pi))\[0.5\]
ซึ่งเป็นค่าที่ถูกต้องตามทฤษฏี
4.5 แบบฝึกหัดอินทิกรัลในเศรษฐศาสตร์
ให้ใช้ caracas ในการหาคำตอบ
เส้นอุปสงค์ของสินค้าคือ \(P = 100 - 2Q\) และราคาตลาดคือ \(P = 60\) จงหาพื้นที่ส่วนเกินของผู้บริโภค (Consumer Surplus)
สมการอุปทานคือ \(P = 10 + Q\) และราคาตลาดคือ \(P = 40\) จงหาส่วนเกินผู้ผลิต (Producer Surplus)
ฟังก์ชันต้นทุนเพิ่ม (Marginal Cost) คือ \(MC(Q) = 6Q\) จงหาต้นทุนรวมในการผลิต 5 หน่วย
ฟังก์ชันรายได้เพิ่ม (Marginal Revenue) คือ \(MR(Q) = 100 - 4Q\) จงหาค่ารายได้รวมเมื่อขาย 10 หน่วย
สมการอุปสงค์คือ \(P = 80 - Q\), จงคำนวณ Consumer Surplus เมื่อราคาตลาดคือ 50
กำหนดฟังก์ชันต้นทุนเฉลี่ย \(AC(Q) = 20 + \frac{100}{Q}\) จงหาต้นทุนรวมเมื่อผลิต 5 หน่วย โดยใช้การอินทิกรัล
รายได้รวมจากการขายคือ \(R(Q) = Q(60 - Q)\) จงหาผลรวมรายได้จากการขายสินค้าจำนวน 0 ถึง 10 หน่วย
พื้นที่ใต้เส้นโค้ง \(f(x) = x^2 + 3x\) จาก \(x = 1\) ถึง \(x = 5\) คือเท่าใด?
ให้ \(C'(Q) = 4Q^2 + 2\) คือ MC จงหาค่า \(TC(Q)\) โดยการอินทิกรัล และหา \(TC\) เมื่อ \(Q = 3\)
ผู้ผลิตมีรายได้ต่อหน่วย \(P = 50\), ขายได้ \(Q = 0\) ถึง \(Q = 20\) หน่วย จงหาผลรวมรายได้ทั้งหมดด้วยอินทิกรัล
ฟังก์ชัน \(f(x) = e^{-x}\) ให้คำนวณพื้นที่ใต้เส้นกราฟจาก \(x = 0\) ถึง \(x = 1\)
ถ้าผู้บริโภคได้รับอรรถประโยชน์ตามฟังก์ชัน \(U(Q) = \int_0^Q (100 - 2q) dq\) จงหา \(U(20)\)
ถ้า \(MC(Q) = 5\), จงคำนวณต้นทุนรวมในการผลิต 10 หน่วย
ให้ \(MR(Q) = 200 - 10Q\) หาผลรวมรายได้ (TR) เมื่อ \(Q = 0\) ถึง \(Q = 15\)
ฟังก์ชัน \(f(q) = \ln(q+1)\) คำนวณพื้นที่ใต้เส้นกราฟนี้จาก \(q = 0\) ถึง \(q = 3\)
ถ้าอุปสงค์คือ \(P = 120 - 3Q\), ราคาตลาดคือ \(P = 60\) จงหาส่วนเกินผู้บริโภค
ผู้ผลิตมีต้นทุนเพิ่ม \(MC = 2Q + 5\), ไม่มีต้นทุนคงที่ หาค่าต้นทุนรวมเมื่อผลิต 8 หน่วย
ถ้าฟังก์ชันผลผลิตชายขอบคือ \(MP(L) = 10 - 0.5L\), ให้หาผลผลิตรวมเมื่อใช้แรงงาน 0 ถึง 10 หน่วย
เส้นอุปสงค์และอุปทานตัดกันที่ \(Q = 20\), ให้ \(P_d = 100 - Q\), \(P_s = 20 + Q\) จงหาส่วนเกินผู้บริโภคและผู้ผลิต
ถ้ารายได้เฉลี่ย \(AR(Q) = 60 - 0.5Q\), จงหาผลรวมรายได้ทั้งหมดจาก 0 ถึง 20 หน่วย