5  การหาค่าสูงสุด/ต่ำสุดภายใต้ข้อจำกัด (Constrained Optimization)

5.1 บทนำ

ในทางเศรษฐศาสตร์ นักเศรษฐศาสตร์มักต้องการหาค่า สูงสุด (maximize) หรือ ต่ำสุด (minimize) ของฟังก์ชัน เช่น:

• ผู้บริโภค: ต้องการเพิ่มอรรถประโยชน์สูงสุด ภายใต้ข้อจำกัดงบประมาณ

• ผู้ผลิต: ต้องการลดต้นทุนให้น้อยที่สุด ภายใต้ข้อจำกัดการผลิต

ปัญหานี้เรียกว่า Constrained Optimization

วิธีแก้ปัญหาหลักคือ Lagrange Multiplier Method หรือภาษาไทยเรียกว่า ตัวคูณลากรองช์

ก่อนที่จะกล่าวถึงหัวข้อตัวคูณลากรองซ์ ในบทที่ 2 ผู้อ่านได้เรียนรู้ถึงการประยุกต์อนุพันธ์ เพื่อหาค่าสูงสุด/ต่ำสุดของฟังก์ชันมาแล้ว ในบทนี้จะมีตัวแปรตั้งแต่ 2 ตัวขึ้นทำให้ ผู้อ่านต้องการเรื่องหาอนุพันธ์บางส่วนของฟังก์ชันก่อน

5.2 อนุพันธ์บางส่วน (Partial Derivative)

นิยาม

ให้ \(f: \mathbb{R}^n \to \mathbb{R}\) เป็นฟังก์ชันที่มีตัวแปรหลายตัว เช่น \(f(x_1, x_2, \ldots, x_n)\)
และเลือกตัวแปร \(x_i\) ตัวใดตัวหนึ่ง

อนุพันธ์บางส่วนของ \(f\) เทียบกับ \(x_i\) คือ

\[ \frac{\partial f}{\partial x_i}(x_1, x_2, \ldots, x_n) = \lim_{h \to 0} \frac{f(x_1, \ldots, x_i + h, \ldots, x_n) - f(x_1, \ldots, x_i, \ldots, x_n)}{h} \]

นั่นคือ

• เปลี่ยนเฉพาะ \(x_i\) ให้เล็กน้อย (จาก \(x_i\) เป็น \(x_i + h\))

• ส่วนตัวแปรอื่น ๆ \(x_j\) (สำหรับ \(j \neq i\)) ตรึง (fix) ไว้ไม่เปลี่ยน

• แล้ววัดอัตราการเปลี่ยนแปลงของ \(f\) เมื่อ \(h\) \(\rightarrow\) 0

ตัวอย่าง

ให้ \(f(x,y) = x^2 + xy + y^2\) อนุพันธ์บางส่วนของ \(f\) ตาม \(x\): \[\frac{\partial f}{\partial x} = 2x + y\] เพราะถือว่า \(y\) เป็นค่าคงที่

อนุพันธ์บางส่วนของ \(f\) ตาม \(y\): \[\frac{\partial f}{\partial y} = x + 2y\] เพราะถือว่า \(x\) เป็นค่าคงที่

หมายเหตุ

• ฟังก์ชัน \(f\) ต้อง นิยามได้ และ ต่อเนื่อง (อย่างน้อยในบริเวณใกล้เคียง)

• ถ้าอนุพันธ์บางส่วนของ \(f\) มีอยู่ทุกตัวแปร แล้วต่อเนื่อง \(\rightarrow\) ฟังก์ชันนี้ differentiable ตามนิยาม

5.3 เกรเดียนต์ (Gradient)

เกรเดียนต์ คือ เวกเตอร์ที่รวมอนุพันธ์บางส่วนทั้งหมดของฟังก์ชัน เข้าด้วยกัน

นิยาม

ถ้าให้ \(f(x_1, x_2, \ldots, x_n)\) เป็นฟังก์ชันจาก \(\mathbb{R}^n\) ไป \(\mathbb{R}\)
เกรเดียนต์ ของ \(f\) นิยามว่า:

\[ \nabla f(x_1, x_2, \ldots, x_n) = \left( \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \ldots, \frac{\partial f}{\partial x_n} \right) \]

อ่านว่า “del f” (เดล เอฟ)

• แต่ละ อนุพันธ์บางส่วน วัด “การเปลี่ยนแปลงของฟังก์ชัน” ตามตัวแปรหนึ่งตัว

• เมื่อเอาทุกตัวมารวมกันเป็น เวกเตอร์ ก็ได้ เกรเดียนต์

• เกรเดียนต์ ชี้ทิศทางที่ฟังก์ชันเพิ่มขึ้นเร็วที่สุด

(เช่น เดินไปตาม เกรเดียนต์ จะไปทางที่ “ฟังก์ชันโตเร็วที่สุด”)

จากตัวอย่างที่ผ่านมา \(f(x,y) = x^2 + xy + y^2\) เกรเดียนต์ คือ: \[\nabla f(x,y) = (2x + y, x + 2y)\] เป็นเวกเตอร์ 2 มิติ

คุณสมบัติสำคัญของเกรเดียนต์

คุณสมบัติ	อธิบาย
ทิศทาง	ชี้ไปในทิศทางที่ \(f\) เพิ่มขึ้นเร็วที่สุด
ความยาว (norm)	บอกอัตราความชัน หรือความเร็วของการเพิ่มขึ้น
ถ้า \(\nabla f = 0\)	จุดนั้นอาจเป็น maximum, minimum, หรือ saddle point (critical point)

5.4 การคำนวณเชิงสัญลักษณ์ของอนุพันธ์บางส่วนด้วย caracas

1. เรียกใช้ชุดคำสั่ง caracas

library(caracas)

จากตัวอย่าง \(f(x,y) = x^2 + xy + y^2\) สามารถสร้างได้ดังนี้

2. กำหนดตัวแปรและฟังก์ชันที่ต้องการ

x <- symbol("x")
y <- symbol("y")
f <- x^2+x*y+y^2
f

\[x^{2} + x y + y^{2}\]

3. หาอนุพันธ์บางส่วนด้วยฟังก์ชัน der()

หา \(\frac{\partial f}{\partial x}\)

der(f, x)

\[2 x + y\]

หา \(\frac{\partial f}{\partial y}\)

der(f, y)

\[x + 2 y\]

ส่วนคำนวณเกรเดียนต์ด้วย caracas ก็ยังใช้คำสั่ง der() เช่นเดิม แต่เปลี่ยนกับใส่ตััวแปรให้อยู่ในของ list แทน และแสดงผลในรูปของเมตริกซ์ขนาด \(1\times n\) โดยที่ \(n\) คือ จำนวนตัวแปรในฟังก์ชัน เช่น ตัวอย่างที่ผ่านมาฟังก์ชัน f ตัวแปร \(x\) และ \(y\)

der(f, list(x,y))

\[\left[\begin{matrix}2 x + y & x + 2 y\end{matrix}\right]\]

5.4.1 การสร้างตัวแปรเป็นจำนวนมากด้วย caracas

ในหลายๆปัญหาทางเศรษฐศาสตร์ นิยมสร้างตัวเป็นลำดับ (sequence) เช่น \(x_1, x_2, \cdots, x_10\) เป็นต้น ถ้าต้องการสร้างตัวแปรลักษณะนี้ด้วย caracas สามารถทำได้ ด้วยคำสั่ง as_sym() สามารถเปลี่ยนเวคเตอร์และเมตริกซ์ในอาร์ เป็นตัวแปรของ caracas ได้

# สร้างเวคเตอร์ p เก็บค่า p1 .. p5
p <- paste0("p", 1:5)
# เปลี่ยนเวคเตอร์เป็นตัวแปร caracas ด้วย as_sym()
p <- as_sym(p)
entropy <- -sum(p*log(p)) 
entropy

\[- p_{1} \log{\left(p_{1} \right)} - p_{2} \log{\left(p_{2} \right)} - p_{3} \log{\left(p_{3} \right)} - p_{4} \log{\left(p_{4} \right)} - p_{5} \log{\left(p_{5} \right)}\]

ทดลองหาค่าเกรเดียนต์

der(entropy, p)

\[\left[\begin{matrix}- \log{\left(p_{1} \right)} - 1 & - \log{\left(p_{2} \right)} - 1 & - \log{\left(p_{3} \right)} - 1 & - \log{\left(p_{4} \right)} - 1 & - \log{\left(p_{5} \right)} - 1\end{matrix}\right]\]

5.5 การหาค่าสูงสุด/ต่ำสุดของฟังก์ชันและไม่มีข้อจำกัด (Unconstrained Optimization)

หัวข้อนี้ฟังก์ชันจะต้องมีตั้งแต่ 2 ตัวแปรขึ้นไปมีขั้นตอนการทำดังนี้

1. กำหนดปัญหา (Problem Statement) โดยระบุชัดเจนว่าเราต้องการหา

   • ค่ามากที่สุด (Maximize) หรือ

   • ค่าน้อยที่สุด (Minimize)

ของฟังก์ชัน \(f(x)\) หรือ \(f(x,y)\) หรือหลายตัวแปร

ตัวอย่าง \[ \text{maximize} \quad f(x,y) = 5x + 4y - x^2 - y^2 \]

2. หา First-Order Conditions (FOC) โดย

   • หา อนุพันธ์ ลำดับที่ 1 ของ \(f\) ตามตัวแปรทุกตัว

   • ตั้งสมการว่า อนุพันธ์เท่ากับศูนย์ (Critical Points)

กรณี 1 ตัวแปร:
\[ f'(x) = 0 \]

กรณีหลายตัวแปร:
\[ \frac{\partial f}{\partial x} = 0, \quad \frac{\partial f}{\partial y} = 0 \] (หรือถ้ามี 3 ตัวแปรก็ครบ 3 สมการ)

หมายเหตุ: จุดที่อนุพันธ์เป็นศูนย์ คือ จุดที่อาจเป็นจุดสูงสุดหรือต่ำสุด (critical point)

3. แก้สมการหา Critical Points

   • แก้สมการที่ได้จากข้อ 2 เพื่อหา \(x\), \(y\) (หรือ ตัวแปรอื่น ๆ)

(ถ้าไม่ใช้โปรแกรมช่วย ในประสบการณ์ผู้เขียน นักส่วนใหญ่ทำได้ แต่มักแก้สมการผิด)

4. ตรวจสอบลักษณะจุด (Second-Order Conditions - SOC)

กรณี 1 ตัวแปร

ดูค่า \(f''(x)\)

• ถ้า \(f''(x) > 0\) \(\rightarrow\) จุดนั้นเป็น จุดต่ำสุด (minimum)

• ถ้า \(f''(x) < 0\) \(\rightarrow\) จุดนั้นเป็น จุดสูงสุด (maximum)

กรณีหลายตัวแปร:

สร้าง Hessian Matrix (เมตริกซ์ของอนุพันธ์ลำดับที่สอง)

ตัวอย่าง Hessian Matrix: \[ H = \begin{bmatrix} \frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} \\ \frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^2 f}{\partial y^2} \end{bmatrix} \]

แล้วพิจารณา positive definite / negative definite ของ Hessian:

• ถ้า Hessian เป็นบวกแน่นอน (Positive Definite) \(\rightarrow\) จุดนั้นเป็น minimum

• ถ้า Hessian เป็นลบแน่นอน (Negative Definite) \(\rightarrow\) จุดนั้นเป็น maximum

วิธีการตรวจสอบ

เงื่อนไข	ผลลัพธ์
\(\det(H) > 0\), \(\frac{\partial^2 f}{\partial x^2} > 0\)	Minimum
\(\det(H) > 0\), \(\frac{\partial^2 f}{\partial x^2} < 0\)	Maximum
\(\det(H) < 0\)	Saddle point
\(\det(H) = 0\)	ต้องวิเคราะห์เพิ่มเติม

หมายเหตุ \(\frac{\partial^2 f}{\partial x^2} > 0\)คือ ค่า diagonal ใน hessian ทุกตัว \(~ >0\) หรือ \(\frac{\partial^2 f}{\partial x^2} < 0\) คือ ค่า diagonal ใน hessian ทุกตัว $ <0$

5. สรุปผล ระบุว่า Critical Point ที่หาได้ เป็น maximum หรือ minimum หรือเป็น saddle point (ถ้าไม่แน่นอน)

5.5.1 สรุปขั้นตอนการคำนวณ

ขั้นตอน	ทำอะไร	หมายเหตุ
1	กำหนดปัญหา	maximize หรือ minimize ฟังก์ชันไหน
2	หา FOC	ตั้งอนุพันธ์ = 0
3	แก้หา Critical Points	ได้ค่า \(x, y\)
4	ตรวจสอบ SOC	ด้วย \(f''\) หรือ Hessian
5	สรุปผลลัพธ์	ว่าเป็นจุดสูงสุด/ต่ำสุดหรือไม่

จากโจทย์ตัวอย่าง

หา maximum/minimum ของ \(f(x,y) = 3x^2 + 2xy + y^2 - 4x - 5y\)

ตามขั้นตอน 1. หาอนุพันธ์หรือเกรเดียนต์ \[\begin{aligned} \frac{\partial f}{\partial x} =& 6x + 2y - 4\\ \frac{\partial f}{\partial y} =& 2x + 2y - 5 \end{aligned}\]

2. ตั้ง FOC: \[\begin{aligned} 6x + 2y - 4 =& 0\\ 2x + 2y - 5 =& 0 \end{aligned}\]

3. แก้ระบบสมการ \(\rightarrow\) ได้ \(x=-1/4, y =11/4)\)

4. ตรวจ Hessian: \[H = \begin{bmatrix} 6 & 2 \\ 2 & 2 \end{bmatrix}\]

\(\rightarrow\) คำนวณ determinant > 0 และ \(\frac{\partial^2 f}{\partial x^2} = 6 > 0\)

5. สรุปผล เป็น minimum

กว่าจะได้คำตอบเหนื่อยจัง ถูกรึเปล่าก็ยังไม่รู้

5.5.2 การทำ 4 ขั้นตอนแรกด้วย caracas

1. สร้างฟังก์ชัน \(f(x,y) = 3x^2 + 2xy + y^2 - 4x - 5y\)

x <- symbol("x")
y <- symbol("y")
# สร้างฟังก์ชัน หาค่าต่ำสุดของ f
min_f <- 3*x^2 + 2*x*y + y^2 - 4*x - 5*y
min_f

\[3 x^{2} + 2 x y - 4 x + y^{2} - 5 y\]

2. ตั้ง FOC: ด้วยการหาเกรเดียนต์ด้วย der()

Gmin_f <- der(min_f, list(x,y))
Gmin_f

\[\left[\begin{matrix}6 x + 2 y - 4 & 2 x + 2 y - 5\end{matrix}\right]\]

3. แก้สมการหา Critical Points ด้วยคำสั่ง solve_sys()

solve_sys(Gmin_f, list(x,y))

Solution 1:
  x =  -1/4 
  y =  11/4 

4. ตรวจสอบคำตอบด้วย Hessian Matrix ถ้าใช้ caracas มีฟังก์ชันชื่อ hessian() ช่วยหา

# หา hessian จากฟังก์ชันข้อ 1 โดยตั้งชื่อ hes.M
hes.M <-hessian(min_f, list(x, y))
hes.M

\[\left[\begin{matrix}6 & 2\\2 & 2\end{matrix}\right]\]

ค่า diagonal ทุกตัวมากกว่า 0

5. หาค่า det เพื่อสรุปผล

det(hes.M)

\[8\]

ดีเทอมิแนนท์มีค่ามากกว่า 0 แสดงว่าเป็นจุดต่ำสุด

ที่จุด \(f(-1/4,11/4)\) มีค่าต่ำสุดเท่ากับ

subs(min_f, list(x = -1/4, y =11/4))

\[-6.375\]

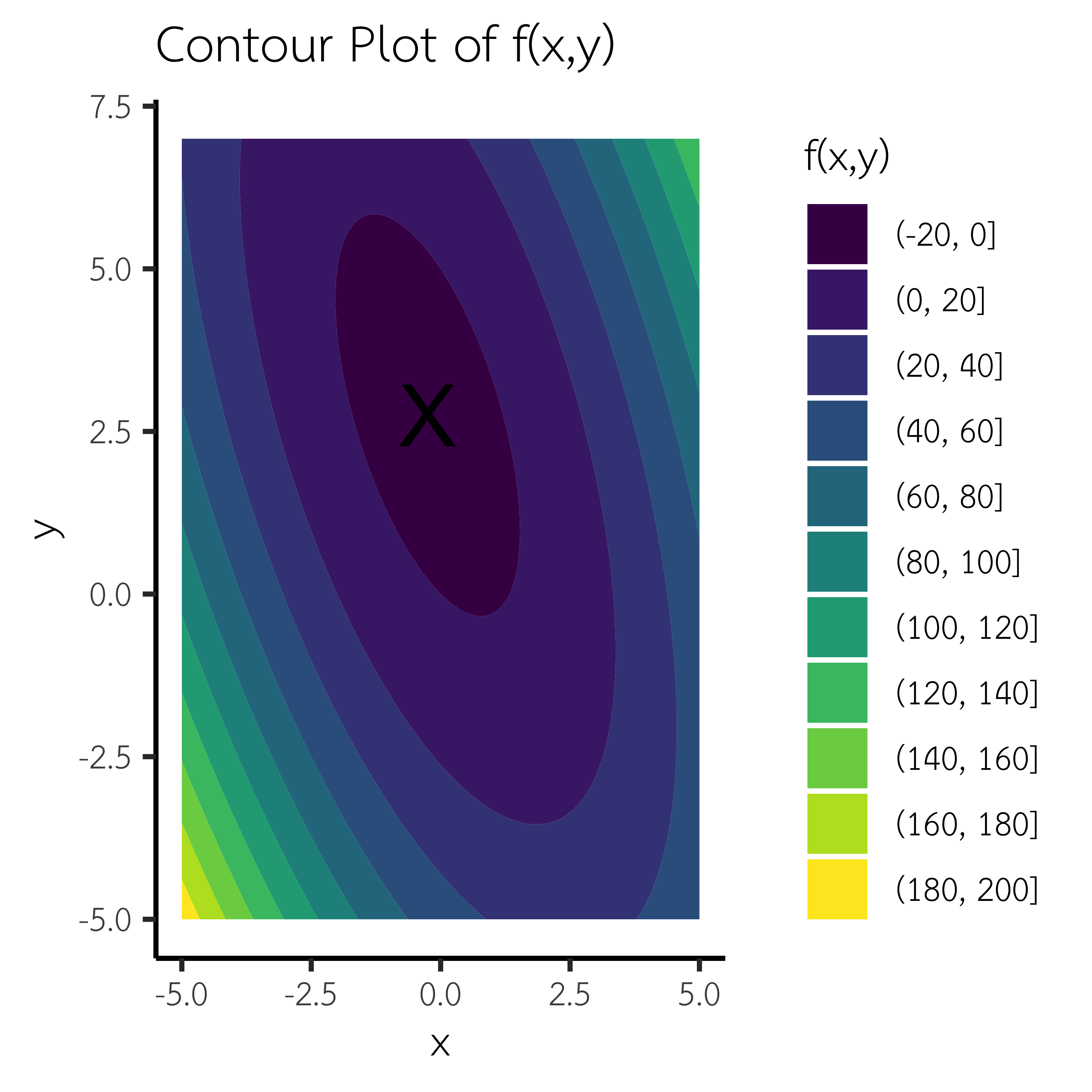
ลองวาดแผนภาพเส้นชั้นความสูง (contour plot) ด้วยอาร์ด้วย ggplot2

# เปลี่ยนฟังก์ชันจาก caracas เป็น ฟังก์ชันใน R ด้วย as_func()
plot.f  <- as_func(min_f)
# โหลดแพ็กเกจที่จำเป็น
library(ggplot2)

# กำหนดช่วงของ x และ y
x <- seq(-5, 5, length.out = 100)
y <- seq(-5, 7, length.out = 100)

# สร้างตารางค่าที่จะใช้วาด
grid <- expand.grid(x = x, y = y)

# คำนวณค่าฟังก์ชัน f(x,y)
grid$z <- plot.f(grid$x,grid$y)

# วาดกราฟ contour
ggplot(grid, aes(x = x, y = y, z = z)) +
  geom_contour_filled() +   # วาด contour แบบมีไล่สี
  labs(title = "Contour Plot of f(x,y)",
       x = "x",
       y = "y",
       fill = "f(x,y)") +
  theme_classic(base_size = 14)+
  theme(text = element_text(family = "TH Sarabun New", size = 16)) + 
  annotate(geom = "text",x = -1/4, y =11/4, label = "X", size =8)

เครื่องหมาย X แสดงจุดต่ำสุด

ถ้าผู้อ่านสนใจการวาดกราฟด้วยอาร์สามารถศึกษาได้จาก การสร้างภาพนิทัศน์ด้วยภาษาอาร์

สำหรับผู้อ่านจาก HTML book จะเห็นกราฟแบบ interactive

# ติดตั้ง plotly ถ้ายังไม่มี
# install.packages("plotly")
library(plotly)
# สร้างข้อมูล
x_seq <- seq(-5, 7, length.out = 50)
y_seq <- seq(-5, 7, length.out = 50)

z_matrix <- outer(x_seq, y_seq, function(x, y) {
  3*x^2 + 2*x*y + y^2 - 4*x - 5*y
})
# วาด surface plot แบบ interactive
plot_ly(
  x = ~x_seq, y = ~y_seq, z = ~z_matrix
) |>
  add_surface() |>
  layout(
    title = "Surface Plot of f(x,y)",
    scene = list(
      xaxis = list(title = "X"),
      yaxis = list(title = "Y"),
      zaxis = list(title = "f(x,y)")
    )
  )

5.5.3 ตัวอย่างการหาค่าสูงสุดต่ำสุดโดยไม่มีข้อจำกัดในทางเศรษฐศาสตร์เพิ่มเติม

โดยใช้การคำนวณเชิงสัญลักษณ์และวาดกราฟประกอบ

กำไรสูงสุดของฟาร์ม

ฟังก์ชันกำไรของฟาร์มกำหนดโดย \[ \pi(x, y) = 100x + 80y - x^2 - y^2 - xy \]

• \(x\): จำนวนข้าวที่ปลูก

• \(y\): จำนวนข้าวโพดที่ปลูก

จงหาค่า \(x\) และ \(y\) ที่ทำให้กำไรสูงสุด

ทำ 4 ขั้นตอนแรกด้วย caracas

1. สร้างฟังก์ชัน

x <- symbol("x")
y <- symbol("y")
# สร้างฟังก์ชัน หาค่าต่ำสุดของ f
max_Pi <- 100*x +80*y-x^2-y^2 -x*y
max_Pi

\[- x^{2} - x y + 100 x - y^{2} + 80 y\]

2. ตั้ง FOC: ด้วยการหาเกรเดียนต์ด้วย der()

Gmax_Pi <- der(max_Pi, list(x,y))
Gmax_Pi

\[\left[\begin{matrix}- 2 x - y + 100 & - x - 2 y + 80\end{matrix}\right]\]

3. แก้สมการหา Critical Points ด้วยคำสั่ง solve_sys()

solve_sys(Gmax_Pi, list(x,y))

Solution 1:
  x =  40 
  y =  20 

4. ตรวจสอบคำตอบด้วย Hessian Matrix ถ้าใช้ caracas มีฟังก์ชันชื่อ hessian() ช่วยหา

# หา hessian จากฟังก์ชันข้อ 1 โดยตั้งชื่อ hes.M
hes.M <-hessian(max_Pi, list(x, y))
hes.M

\[\left[\begin{matrix}-2 & -1\\-1 & -2\end{matrix}\right]\]

ค่าใน diagonal ทุกตัวน้อยกว่า 0

5. หาค่า det เพื่อสรุปผล

det(hes.M)

\[3\]

ดีเทอมิแนนท์มีค่าเท่ากับ 3 มากกว่า 0 แสดงว่าเป็นจุดสูงสุด ที่จุด \(\pi(40,20)\) มีค่าสูงสุดเท่ากับ

subs(max_Pi, list(x = 40, y =20))

\[2800\]

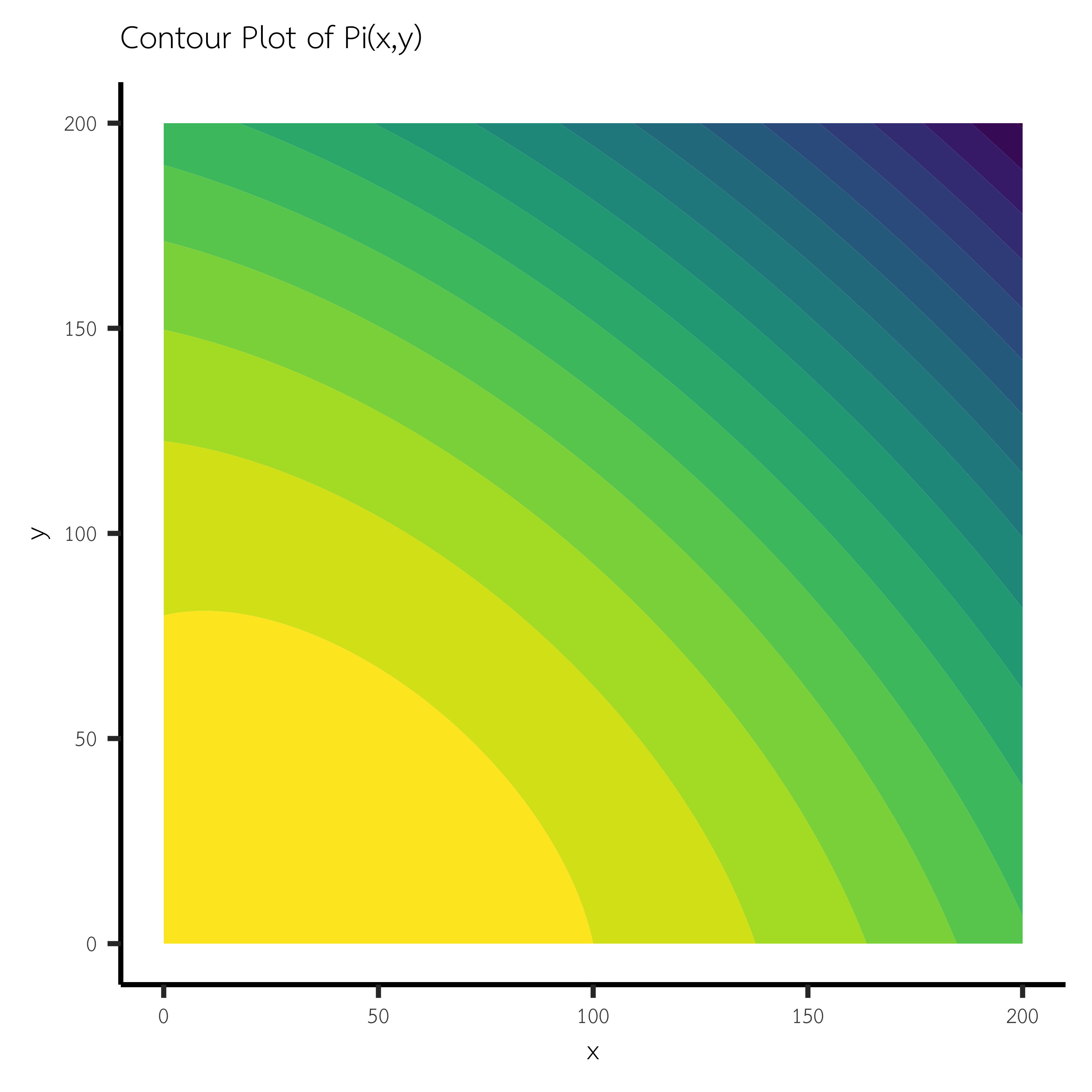
สามารถกราฟ contour และ surfaceเพื่อพิจารณา ฟังก์ชันนี้มีค่าสูงสุด หรือต่ำสุดจริงๆ หรือไม่?

# เปลี่ยนฟังก์ชันจาก caracas เป็น ฟังก์ชันใน R ด้วย as_func()
plot.Pi  <- function(x, y){
return(100*x + 80*y -x^2 - y^2 - x*y)  
}
# โหลดแพ็กเกจที่จำเป็น
library(ggplot2)

# กำหนดช่วงของ x และ y
x <- seq(0, 200, length.out = 1000)
y <- seq(0, 200, length.out = 1000)

# สร้างตารางค่าที่จะใช้วาด
grid <- expand.grid(x = x, y = y)

# คำนวณค่าฟังก์ชัน f(x,y)
grid$z <- plot.Pi(grid$x,grid$y)

# วาดกราฟ contour
ggplot(grid, aes(x = x, y = y, z = z)) +
  geom_contour_filled(bins = 20) +   # วาด contour แบบมีไล่สี
  labs(title = "Contour Plot of Pi(x,y)",
       x = "x",
       y = "y",
       fill = "f(x,y)") +
  theme_classic(base_size = 14)+
  theme(legend.position = "none", # นำ legend ออก
        text = element_text(family = "TH Sarabun New", size = 10))

เครื่องหมาย X แสดงจุดต่ำสุด

วาด surface plot

# ติดตั้ง plotly ถ้ายังไม่มี
# install.packages("plotly")
library(plotly)
# สร้างข้อมูล
x_seq <- seq(0, 200, length.out = 200)
y_seq <- seq(0, 200, length.out = 200)

z_matrix <- outer(x_seq, y_seq, plot.Pi)
# วาด surface plot แบบ interactive
plot_ly(
  x = ~x_seq, y = ~y_seq, z = ~z_matrix
) |>
  add_surface() |>
  layout(
    title = "Surface Plot of f(x,y)",
    scene = list(
      xaxis = list(title = "X"),
      yaxis = list(title = "Y"),
      zaxis = list(title = "f(x,y)")
    )
  )

เหตุผลที่ไม่วากราฟก่อนคำนวณ การการกำหนดความช่วงที่พิจารณา ถ้า กำหนดความช่วงกว้างเกินไป อาจจะเห็นไม่ชัดเจน และถ้ากำหนดความยาวช่วงสั้นเกินไป ก็อาจจะไม่ไม่รวมคำตอบอยู่ในกราฟก็ได้

ต้นทุนต่ำสุดของโรงงาน

ฟังก์ชันต้นทุนของโรงงานคือ

\[ C(K, L) = K^2 + 2KL + 3L^2 - 20K - 30L \]

• \(K\): หน่วยทุน

• \(L\): หน่วยแรงงาน

จงหาจำนวน \(K\) และ \(L\) ที่ทำให้ต้นทุนต่ำสุด

ทำ 4 ขั้นตอนแรกด้วย caracas

1. สร้างฟังก์ชัน

K <- symbol("K")
L <- symbol("L")
# สร้างฟังก์ชัน หาค่าต่ำสุดของ f
min_C <- K^2 +2*K*L +3*L^2 -20*K -30*L
min_C

\[K^{2} + 2 K L - 20 K + 3 L^{2} - 30 L\]

2. ตั้ง FOC: ด้วยการหาเกรเดียนต์ด้วย der()

Gmin_C <- der(min_C, list(K,L))
Gmin_C

\[\left[\begin{matrix}2 K + 2 L - 20 & 2 K + 6 L - 30\end{matrix}\right]\]

3. แก้สมการหา Critical Points ด้วยคำสั่ง solve_sys()

solve_sys(Gmin_C, list(K,L))

Solution 1:
  K =  15/2 
  L =  5/2 

4. ตรวจสอบคำตอบด้วย Hessian Matrix ถ้าใช้ caracas มีฟังก์ชันชื่อ hessian() ช่วยหา

# หา hessian จากฟังก์ชันข้อ 1 โดยตั้งชื่อ hes.M
hes.M <-hessian(min_C, list(K,L))
hes.M

\[\left[\begin{matrix}2 & 2\\2 & 6\end{matrix}\right]\]

ค่าใน diagonal ทุกตัวมากกว่า 0

5. หาค่า det เพื่อสรุปผล

det(hes.M)

\[8\]

ดีเทอมิแนนท์มีค่าเท่ากับ 8 มากกว่า 0 แสดงว่าเป็นจุดต่ำสุด ที่จุด \(C(15/2,5/2)\) มีค่าสูงสุดเท่ากับ

subs(min_C, list(K = 15/2, L = 5/2))

\[-112.5\]

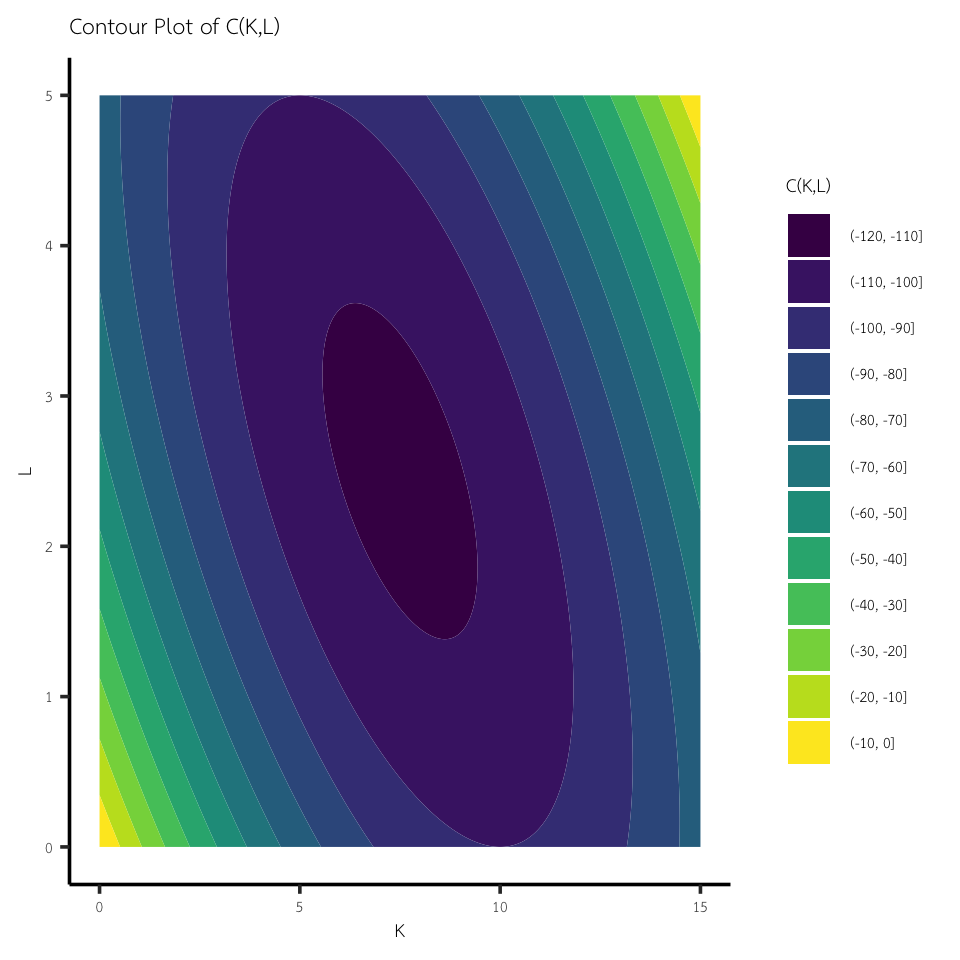
สามารถกราฟ contour และ surfaceเพื่อพิจารณา ฟังก์ชันนี้มีค่าสูงสุด หรือต่ำสุดจริงๆ หรือไม่?

#| fig-format: png
#| fig-dpi: 400
# เปลี่ยนฟังก์ชันจาก caracas เป็น ฟังก์ชันใน R ด้วย as_func()
plot.C  <- function(K, L){
return(K^2 +2*K*L +3*L^2 -20*K -30*L)  
}
# โหลดแพ็กเกจที่จำเป็น
library(ggplot2)

# กำหนดช่วงของ x และ y
x <- seq(0, 15, length.out = 1000)
y <- seq(0, 5, length.out = 1000)

# สร้างตารางค่าที่จะใช้วาด
grid <- expand.grid(x = x, y = y)
# คำนวณค่าฟังก์ชัน f(x,y)
grid$z <- plot.C(grid$x,grid$y)
# วาดกราฟ contour
ggplot(grid, aes(x = x, y = y, z = z)) +
  geom_contour_filled() +   # วาด contour แบบมีไล่สี
  labs(title = "Contour Plot of C(K,L)",
       x = "K",
       y = "L",
       fill = "C(K,L)") +
  theme_classic(base_size = 14)+
  theme(text = element_text(family = "TH Sarabun New", size = 10))

วาด surface plot

# ติดตั้ง plotly ถ้ายังไม่มี
# install.packages("plotly")
library(plotly)
# สร้างข้อมูล
x_seq <- seq(0, 15, length.out = 200)
y_seq <- seq(0, 5, length.out = 200)

z_matrix <- outer(x_seq, y_seq, plot.C)
# วาด surface plot แบบ interactive
plot_ly(
  x = ~x_seq, y = ~y_seq, z = ~z_matrix
) |>
  add_surface() |>
  layout(
    title = "Surface Plot of C(K,L)",
    scene = list(
      xaxis = list(title = "K"),
      yaxis = list(title = "L"),
      zaxis = list(title = "C(K,L)")
    )
  )

อรรถประโยชน์ของผู้บริโภค (Utility Maximization)

ฟังก์ชันอรรถประโยชน์ของผู้บริโภคคือ

\[ U(x_1, x_2) = 4x_1 - x_1^2 + 3x_2 - x_2^2 \]

หาค่า \(x_1\) และ \(x_2\) ที่ทำให้อรรถประโยชน์สูงสุด

ทำ 4 ขั้นตอนแรกด้วย caracas

1. สร้างฟังก์ชัน

# สร้างเวคเตอร์ ตัวแปร
x <- paste0("x",1:2)
x <- as_sym(x)
# สร้างฟังก์ชัน หาค่าสูงสุด
max_U <- 4*x[1]-x[1]^2 +3*x[2]-x[2]^2
max_U

\[- x_{1}^{2} + 4 x_{1} - x_{2}^{2} + 3 x_{2}\]

2. ตั้ง FOC: ด้วยการหาเกรเดียนต์ด้วย der()

Gmax_U <- der(max_U, x)
Gmax_U

\[\left[\begin{matrix}4 - 2 x_{1} & 3 - 2 x_{2}\end{matrix}\right]\]

3. แก้สมการหา Critical Points ด้วยคำสั่ง solve_sys()

solve_sys(Gmax_U, x)

Solution 1:
  x1 =  2 
  x2 =  3/2 

4. ตรวจสอบคำตอบด้วย Hessian Matrix ถ้าใช้ caracas มีฟังก์ชันชื่อ hessian() ช่วยหา

# หา hessian จากฟังก์ชันข้อ 1 โดยตั้งชื่อ hes.M
hes.M <-hessian(max_U, x)
hes.M

\[\left[\begin{matrix}-2 & 0\\0 & -2\end{matrix}\right]\]

ค่าใน diagonal ทุกตัวน้อยกว่า 0

5. หาค่า det เพื่อสรุปผล

det(hes.M)

\[4\]

ดีเทอมิแนนท์มีค่าเท่ากับ 8 มากกว่า 0 แสดงว่าเป็นจุดสูงสุด ที่จุด \(U(2,3/2)\) มีค่าสูงสุดเท่ากับ

subs(max_U, x,c(2,3/2))

\[6.25\]

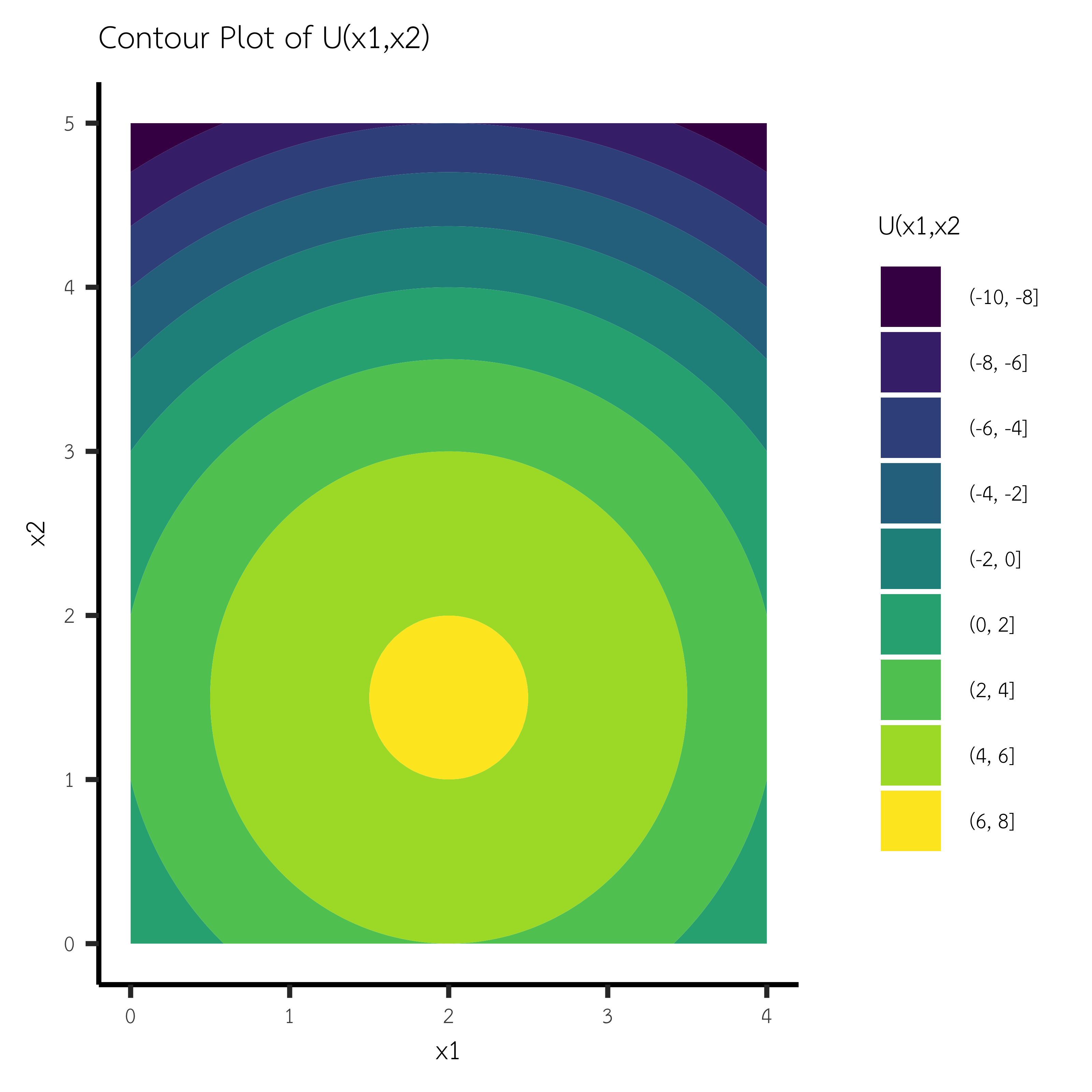
สามารถกราฟ contour และ surfaceเพื่อพิจารณา ฟังก์ชันนี้มีค่าสูงสุด หรือต่ำสุดจริงๆ หรือไม่?

# เปลี่ยนฟังก์ชันจาก caracas เป็น ฟังก์ชันใน R ด้วย as_func()
plot.U  <- function(x1,x2){
return(4*x1-x1^2 +3*x2-x2^2)  
}
# โหลดแพ็กเกจที่จำเป็น
library(ggplot2)

# กำหนดช่วงของ x และ y
x <- seq(0, 4, length.out = 100)
y <- seq(0, 5, length.out = 100)

# สร้างตารางค่าที่จะใช้วาด
grid <- expand.grid(x = x, y = y)
# คำนวณค่าฟังก์ชัน f(x,y)
grid$z <- plot.U(grid$x,grid$y)
# วาดกราฟ contour
ggplot(grid, aes(x = x, y = y, z = z)) +
  geom_contour_filled() +   # วาด contour แบบมีไล่สี
  labs(title = "Contour Plot of U(x1,x2)",
       x = "x1",
       y = "x2",
       fill = "U(x1,x2") +
  theme_classic(base_size = 14)+
  theme(text = element_text(family = "TH Sarabun New", size = 10))

วาด surface plot

# ติดตั้ง plotly ถ้ายังไม่มี
# install.packages("plotly")
library(plotly)
# สร้างข้อมูล
x_seq <- seq(0, 5, length.out = 200)
y_seq <- seq(0, 5, length.out = 200)

z_matrix <- outer(x_seq, y_seq, plot.U)
# วาด surface plot แบบ interactive
plot_ly(
  x = ~x_seq, y = ~y_seq, z = ~z_matrix
) |>
  add_surface() |>
  layout(
    title = "Surface Plot of U(x1,x2)",
    scene = list(
      xaxis = list(title = "x1"),
      yaxis = list(title = "x2"),
      zaxis = list(title = "U(x1,x2)")
    )
  )

ผลผลิตสูงสุดจากฟังก์ชัน Cobb-Douglas แบบง่าย

ฟังก์ชันการผลิตเป็น \[Q(K, L) = 20K^{0.5}L^{0.5} - 2K - 3L\]

• \(K\): หน่วยทุน

• \(L\): หน่วยแรงงาน

หาค่า \(K\) และ \(L\) ที่ทำให้ผลผลิตสุทธิมากที่สุด

ทำ 4 ขั้นตอนแรกด้วย caracas

1. สร้างฟังก์ชัน

# สร้างเวคเตอร์ ตัวแปร
K <- symbol("K", "positive" = TRUE)
L <- symbol("L", "positive" = TRUE)
# สร้างฟังก์ชัน หาค่าสูงสุด
max_Q <- 20*sqrt(K)*sqrt(L)-2*K -3*L
max_Q

\[20 \sqrt{K} \sqrt{L} - 2 K - 3 L\]

2. ตั้ง FOC: ด้วยการหาเกรเดียนต์ด้วย der()

Gmax_Q <- der(max_Q, list(K,L))
Gmax_Q

\[\left[\begin{matrix}-2 + \frac{10 \sqrt{L}}{\sqrt{K}} & \frac{10 \sqrt{K}}{\sqrt{L}} - 3\end{matrix}\right]\]

3. แก้สมการหา Critical Points ด้วยคำสั่ง solve_sys()

solve_sys(Gmax_Q, list(K,L))

No solutions

สามารถเช็คได้โดยง่ายว่า จากเกรเดียนต์ ไม่สามารถหาคำตอบได้

5.6 การหาค่าสูงสุด/ต่ำสุดของฟังก์ชันและมีข้อจำกัด (Constrained Optimization)

เพราะเศรษฐศาสตร์เกี่ยวข้องกับ “การเลือกภายใต้ข้อจำกัด” (Choice under Scarcity)

• เศรษฐศาสตร์ศึกษา “การเลือก” (choice) ที่เกิดขึ้นเพราะ ทรัพยากรมีจำกัด (scarcity)

• ทุกการตัดสินใจทางเศรษฐกิจ — เช่น การบริโภค การผลิต การลงทุน การกำหนดราคาสินค้า — ล้วนเกิดขึ้นภายใต้ ข้อจำกัด:

  • รายได้จำกัด (budget constraint)

  • ต้นทุนการผลิต

  • เวลาจำกัด

  • กำลังการผลิตจำกัด

  • ทรัพยากรธรรมชาติจำนวนจำกัด

เพราะโลกจริงมีข้อจำกัดเสมอ การทำ optimization ที่ไม่คำนึงถึง constraint จะไม่สะท้อนโลกจริง

ตัวอย่างการใช้ Constrained Optimization ในเศรษฐศาสตร์จริง

สถานการณ์	ฟังก์ชันเป้าหมาย	ข้อจำกัด
การบริโภคของผู้บริโภค	อรรถประโยชน์ (utility maximization)	งบประมาณ (budget constraint)
การผลิตของบริษัท	ผลผลิต (production maximization)	ทุนและแรงงานจำกัด
บริษัทตั้งราคา	กำไร (profit maximization)	กำลังการผลิตหรือข้อกำหนดภาครัฐ
การจัดสรรทรัพยากร	สวัสดิการสังคม (welfare maximization)	งบประมาณรัฐจำกัด
การลงทุน	ผลตอบแทนรวม (return maximization)	ความเสี่ยงหรืองบลงทุนจำกัด

5.6.1 ขั้นตอนการทำ Constrained Optimization

1. กำหนดปัญหา (Problem Definition)

กำหนดฟังก์ชันวัตถุประสงค์ (Objective Function) และข้อจำกัด (Constraint)

• ต้องการหาค่าสูงสุด (maximize) หรือค่าต่ำสุด (minimize) ของฟังก์ชัน \[f(x_1, x_2, \dots, x_n)\] โดยมีข้อจำกัดในรูปแบบ \[g_i(x_1, x_2, \dots, x_n) = 0, \quad i = 1,2,\dots,m\]

หมายเหตุ: ในกรณีนี้พิจารณาเฉพาะข้อจำกัดประเภท “เท่ากับ” (equality constraint)

2. สร้างฟังก์ชันลากรังเชียน (Construct the Lagrangian Function)

นิยามฟังก์ชัน Lagrangian:

\[ \mathcal{L}(x_1, x_2, \dots, x_n, \lambda_1, \lambda_2, \dots, \lambda_m) = f(x_1, x_2, \dots, x_n) + \sum_{i=1}^m \lambda_i (c_i - g_i(x_1, x_2, \dots, x_n)) \]

โดยที่:

• \(\lambda_i\) คือ Lagrange multipliers สำหรับข้อจำกัดแต่ละข้อ

• \(c_i\) คือค่าคงที่ที่ข้อจำกัดแต่ละตัวกำหนด

3. หาเงื่อนไขอันดับหนึ่ง (First-Order Conditions: FOC) ทำการหาอนุพันธ์บางส่วน (partial derivatives) ของฟังก์ชัน Lagrangianแล้วตั้งสมการว่าอนุพันธ์แต่ละตัวเท่ากับศูนย์ สำหรับทุกตัวแปร \(x_j\) และตัวคูณลากรังจ์ \(\lambda_i\): \[\begin{aligned} \frac{\partial \mathcal{L}}{\partial x_j} =& 0, \quad \text{สำหรับทุก } j = 1,2,\dots,n\\ \frac{\partial \mathcal{L}}{\partial \lambda_i} =& 0, \quad \text{สำหรับทุก } i = 1,2,\dots,m \end{aligned}\]

หมายเหตุ: \(\frac{\partial \mathcal{L}}{\partial \lambda_i} = 0\) คือสมการข้อจำกัดเดิม \(g_i(x) = c_i\)

4. แก้ระบบสมการ (Solve the System of Equations)

   • แก้ระบบสมการที่ได้จาก FOC

   • หา \((x_1^*, x_2^*, \dots, x_n^*, \lambda_1^*, \dots, \lambda_m^*)\)

5. ตรวจสอบลักษณะของจุดวิกฤติ (Second-Order Conditions: SOC) ถ้ามีความจำเป็น (โดยเฉพาะกรณีที่ต้องการพิสูจน์ minimum/maximum อย่างละเอียด):

   • ตรวจสอบลักษณะของจุดวิกฤติ โดยการวิเคราะห์ Hessian matrix ของฟังก์ชันวัตถุประสงค์บนข้อจำกัด

   • ใช้วิธี Bordered Hessian Test หรือเทคนิค Second-Order Sufficient Conditions

6. ตีความผลลัพธ์ (Interpret the Solution)

   • สรุปค่า \(x_j^*\) ที่ได้

   • คำนวณค่าของฟังก์ชันวัตถุประสงค์ที่จุดนั้น: \(f(x_1^*, x_2^*, \dots, x_n^*)\)

   • ตีความทางเศรษฐศาสตร์ วิศวกรรม หรือบริบทของปัญหา (เช่น ผลผลิตสูงสุด, ต้นทุนต่ำสุด)

5.7 ตัวอย่างการประยุกต์

5.7.1 การเพิ่มอรรถประโยชน์ภายใต้งบประมาณ (Utility Maximization)

ปัญหา: ให้ฟังก์ชันอรรถประโยชน์ของผู้บริโภค
\[ U(x_1, x_2) = x_1^{0.5} x_2^{0.5} \] โดยข้อจำกัดงบประมาณคือ
\[ p_1x_1 + p_2x_2 = m \] ( \(p_1, p_2\) ราคาสินค้า; \(m\) รายได้)

สร้างฟังก์ชัน Lagrangian: \[ \mathcal{L}(x_1, x_2, \lambda) = x_1^{0.5}x_2^{0.5} + \lambda(m - p_1x_1 - p_2x_2) \]

ตั้งสมการ FOC: \[ \frac{\partial \mathcal{L}}{\partial x_1} = 0 \quad \frac{\partial \mathcal{L}}{\partial x_2} = 0 \quad \frac{\partial \mathcal{L}}{\partial \lambda} = 0 \]

แก้ระบบสมการ จะได้ Demand Functions สำหรับ \(x_1\) และ \(x_2\)

5.4 เงื่อนไข Second-Order (SOC: Second-Order Conditions) - ใช้ตรวจสอบว่าจุดที่หาได้เป็นจุดสูงสุดหรือต่ำสุดจริงหรือไม่ - โดยตรวจสอบลักษณะของ Hessian Matrix ของฟังก์ชัน - ในเศรษฐศาสตร์ปกติเราสนใจเฉพาะกรณีที่ เป็นจุดสูงสุด (Maximization)

5.5 กรณีมีหลายข้อจำกัด (Multiple Constraints)

ถ้ามีมากกว่าหนึ่งข้อจำกัด เช่น
\[ g_1(x) = 0, \quad g_2(x) = 0 \] จะมีตัวแปร Lagrange เพิ่มขึ้น เช่น \(\lambda_1, \lambda_2\) และ Lagrangian ใหม่จะเป็น \[ \mathcal{L}(x, \lambda_1, \lambda_2) = f(x) + \lambda_1(c_1 - g_1(x)) + \lambda_2(c_2 - g_2(x)) \]

5.7.2 การคำนวณเชิงสัญลักษณ์ด้วย caracas

จะเหมือนกับหัวข้อที่ผ่านทุกประการ เพียงแค่ต้องคำนวณว่าผ่านฟังก์ชันลากรองซ์เท่านั้นเอง

ความหมายเชิงเศรษฐศาสตร์ของ Lagrange Multiplier

• ค่า \(\lambda\) แสดงถึง shadow price หรือ มูลค่าทางอ้อม ของข้อจำกัด

• ตัวอย่าง: ถ้า \(\lambda=2\) ในงบประมาณ แปลว่า การมีเงินเพิ่ม 1 หน่วยจะเพิ่มอรรถประโยชน์ได้ 2 หน่วย

5.8 ปัญหาแบบมีข้อจำกัดไม่เท่ากับ (Inequality Constraints) [เพิ่มเติม]

• ใช้เทคนิค Kuhn-Tucker Conditions แทน
• ตัวอย่างเช่น: การผลิตที่มีข้อจำกัดว่าไม่เกินกำลังการผลิตสูงสุด

5.9 สรุป

• ปัญหา Constrained Optimization พบได้ทั่วไปในเศรษฐศาสตร์
• วิธี Lagrange Multiplier เป็นเครื่องมือสำคัญ
• การเข้าใจค่า \(\lambda\) ช่วยตีความผลลัพธ์เชิงเศรษฐศาสตร์ได้ลึกซึ้ง

Andersen, M. M., & Højsgaard, S. (2023). caracas: Computer Algebra. https://github.com/r-cas/caracas

Berkelaar, M. (2024). lpSolve: Interface to ’Lp_solve’ v. 5.5 to Solve Linear/Integer Programs. https://doi.org/10.32614/CRAN.package.lpSolve

Chanaim, S. (2023). Data Visualization with R Programming. https://bookdown.org/somsak_c/data_visualization_with_r_programming/

Meurer, A., Smith, C. P., Paprocki, M., Čertı́k, O., Kirpichev, S. B., Rocklin, M., Kumar, A., Ivanov, S., Moore, J. K., Singh, S., และคณะ. (2017). SymPy: symbolic computing in Python. PeerJ Computer Science, 3, e103. https://doi.org/10.7717/peerj-cs.103

Sievert, C. (2020). Interactive Web-Based Data Visualization with R, plotly, and shiny. Chapman; Hall/CRC. https://plotly-r.com

Ushey, K., Allaire, J., & Tang, Y. (2025). reticulate: Interface to ’Python’. https://doi.org/10.32614/CRAN.package.reticulate

Wickham, H. (2016). ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag New York. https://ggplot2.tidyverse.org