Chapter 3 Lesson 28: Introduction to Ordinary Differential Equations

3.1 Objectives

  1. Understand the definition of an ordinary differential equation (ODE), including order.

  2. Understand the difference between solving an equation and verifying a solution.

  3. Understand that a solution of an ODE is a function, rather than a single input number.

  4. Understand the difference between a specific solution and a general solution of an ODE.

  5. Given an ODE and a function (or family of functions), determine whether the given function (or family of functions) is a solution to the ODE.

  6. Given an ODE and a function containing parameter(s), find the parameter(s) that will make the given function a solution of the ODE.

3.2 In class

  1. Intro. This lesson serves as an introduction to ordinary differential equations (ODEs). The concept of a solution being a function may be difficult for some students to grasp.

  2. General Solution. ODEs can have an infinite number of solutions and we describe them all with a parameter, \(C\).

  3. Specific Solution is one particular function that solves the ODE.

  4. Solution Verification. Given an ODE and a potential solution, we can check if the solution solves the ODE by plugging it into the LHS and RHS of the ODE. If LHS=RHS, then the given function is a solution to the ODE. This can be done algebraically, or by using D, and/or using plotFun.

  5. Order of an ODE. Order of the equation is the order of the highest derivative appearing on the unknown function. On this course we’ll focus on first order ODEs, but have them identify a second and/or third order ODE in this lesson.

3.3 R Commands

makeFun, D, plotFun

3.4 Problems & Activities

  1. Emphasize that differential equations have functions for solutions, not numbers. As an example, consider the differential equation \(\frac{dy}{dt}(t) = 2t\) from the reading. This equation has the general solution of \(y(t) = t^{2} + C\), because the derivative of \(y(t)\) is \(2t\), regardless of what value we choose for \(C\). If you want, spend some time on another example, like \(\frac{dy}{dt}(t) = \cos(t)\).

  2. Consider the differential equation given by \(y^{'}(t) = 2ty(t)\). Emphasize that the right hand side of this expression is a function of the input AND output variables. In today’s lesson, we will not use methods for obtaining solutions. Rather, today, we will focus on determining whether a proposed function could be a solution to a given differential equation. In groups/at board/individually, have cadets determine whether the following two candidate functions are solutions to this ODE: \(y_{1}(t) = t^{2}\) and \(y_{2}(t) = e^{t^{2}}\).

  3. Talk about the difference between a general solution and a specific solution. A general solution is a description of all the functions that solve an ODE. If we can integrate the RHS of the ODE, then we can find the general solution by including the constant of integration. We’ll talk about methods for solving ODEs where the RHS includes \(y\) in a later lesson. In the examples above, we found a few specific solutions just by guessing and checking.

  4. There are lots of methods for verifying whether or not a proposed solution is indeed a solution to the ODE. If you can differentiate by hand and show algebraically that LHS=RHS, then great. If you need to use D to differentiate, that’s disappointing, but fine. If you need to plot LHS and RHS and see if the graphs are the same or different, fine. Take the ODE \[y'=y+e^t.\] is \(y_1=te^t\) a solution to this ODE? If we calculate LHS, \(y_1'\) we get \[LHS=e^t+te^t.\] We could just as well use D to calculate that fact.

y1=makeFun(t*exp(t)~t)
D(y1(t)~t)
## function (t) 
## t * exp(t) + exp(t)

If we calculate the RHS, \(y_1+e^t\), we get \[RHS = te^t+e^t.\] It looks to us like LHS=RHS, so \(y_1\) must be a solution to the ODE. If it were harder to see that LHS=RHS, we could plot the two and see if their graphs overlap.

plotFun(t*exp(t)+exp(t)~t,xlim=c(-5,5),lwd=3,col='maroon')
plotFun(y1(t)+exp(t)~t,lwd=3,col='cadetblue2',add=TRUE)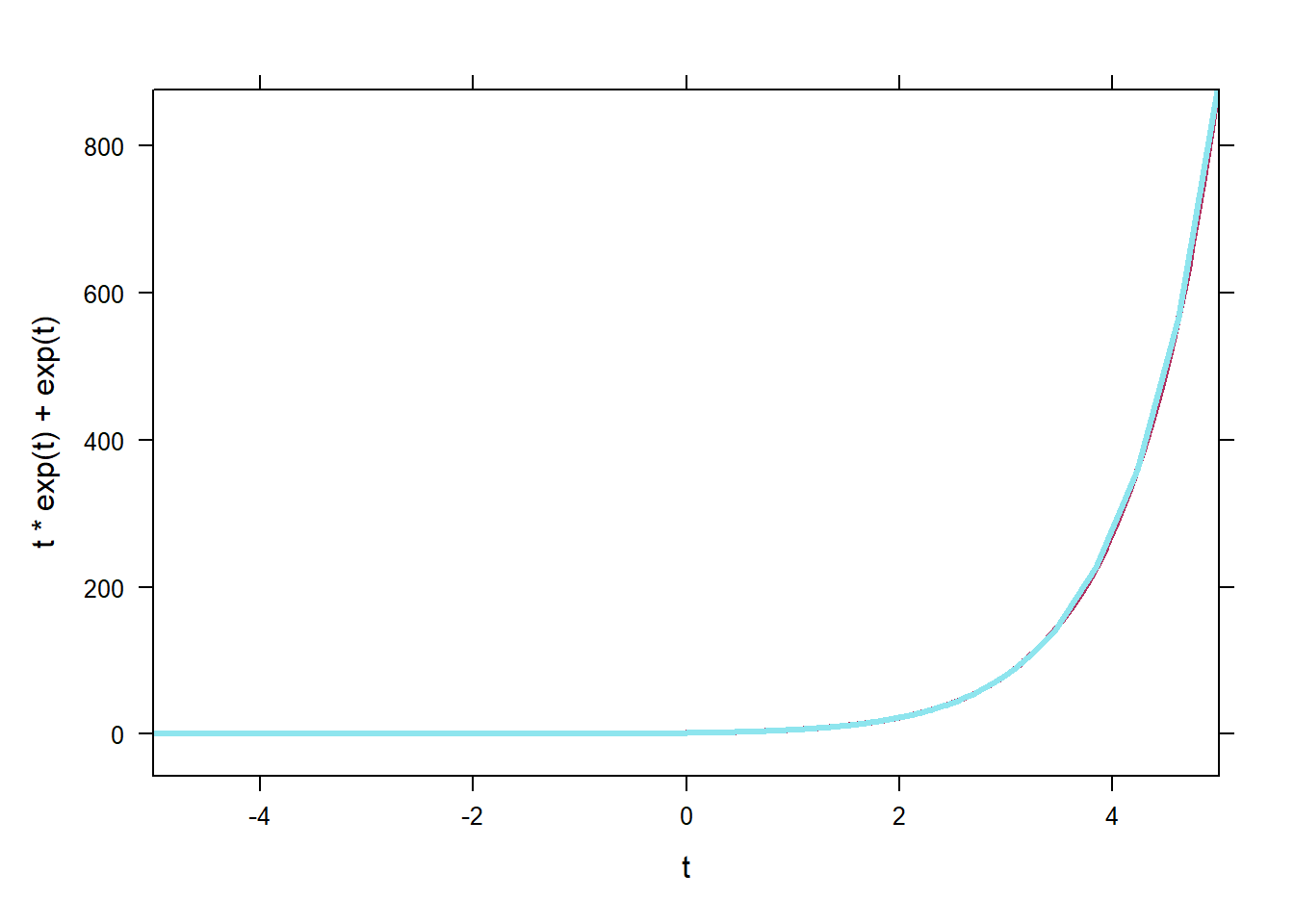

Those graphs seem to be on top of each other, so we reasonably assume that LHS=RHS, and so we think \(y_1\) is a solution to the ODE.

  1. Talk about order of an ODE. The order of an ODE is the order of the highest derivative occurring on the unknown function. The order of \[y'=y+cos(t)\] is one. The order of \[y'=(y'')^4+y\] is two. The order of \[y'''+ty''+\sin(t)y'+4=0\] is three.

    In this class we’ll only solve first order ODE, but order is a very common classification of ODEs, so it is good to have at least heard it before.

  2. Have the students work on problems verifying whether or not proposed solutions are actually solutions to the ODE. The end of the chapter has a ton of them.

  3. Also have students work on determining for what parameter value a proposed solution satisfies an ODE. For example, for what value of \(r\) does \(y_1=e^{rt}\) solve the differential equation \[y'=7y?\]

    For what value of \(c\) does \(y_2=\cos(ct)\) solve the differential equation \[y''=-9y?\] For what value of \(d\) does \(y_3=6t^2+d\) solve the differential equation \[y'=2\left(\frac{y-4}{t}\right)?\]