10.2 Why vote-counting is bad
Imagine there are three studies of the effect of ibuprofen on depressive symptoms. Let’s say that one of them finds a significant effect (ibuprofen significantly reduces symptoms), and two do not. Counting votes, we would say that ‘no effect’ wins by two votes to one. But let’s look at the results more carefully. We can express their parameter estimate in terms of numbers of standard deviations by which the depression scores in the ibuprofen group are lower than those in the control group, and put them onto a forest plot as below.
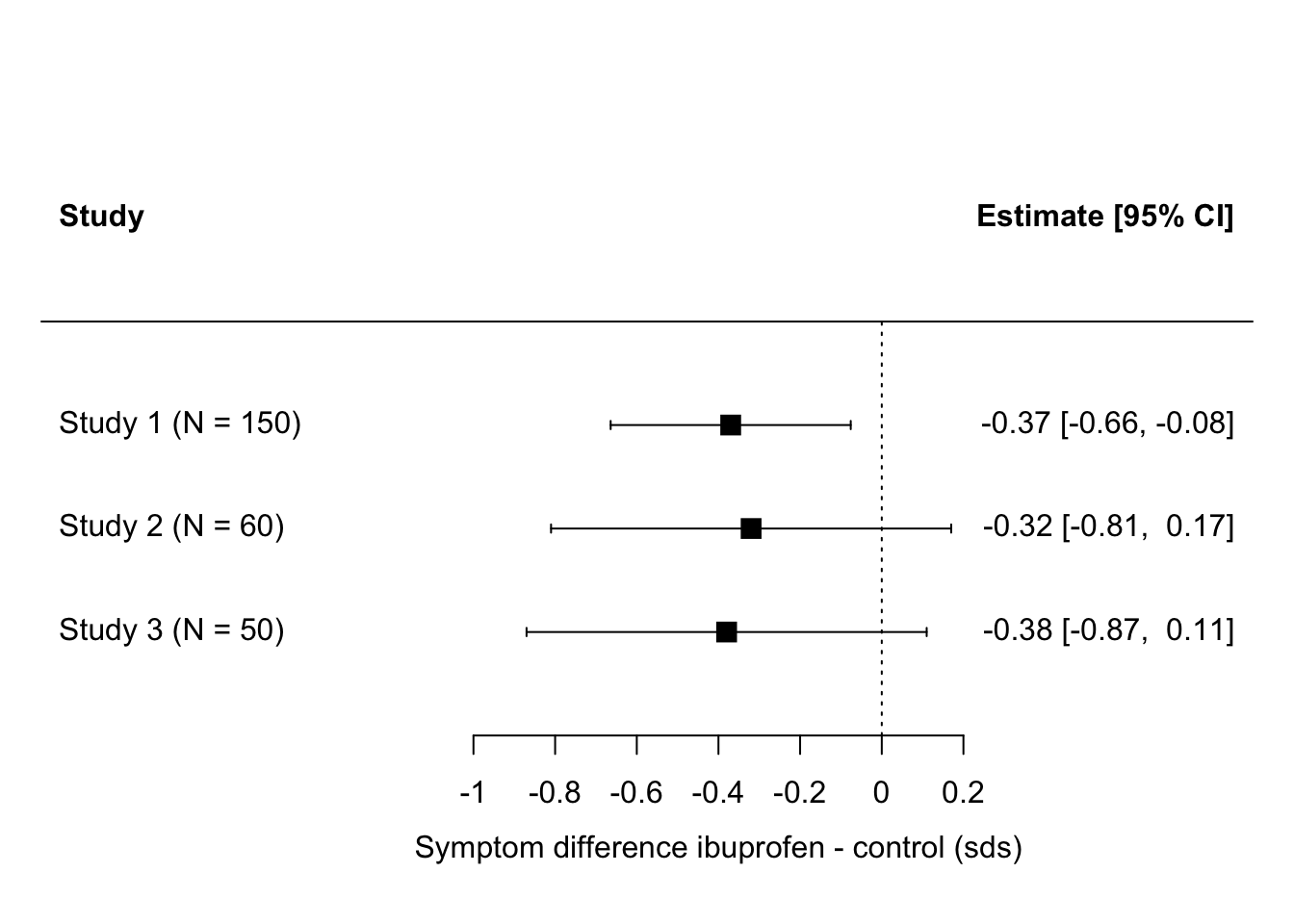
What we immediately see here is that all three studies produce about the same estimate - that ibuprofen produces lower depressive symptoms than control treatment by around 0.3 to 0.4 standard deviations. In study 1, this is enough to be significantly different from zero, because the sample size in study 1 is quite big. Hence the precision of parameter estimation is decent, so the confidence interval is small and does not include zero. Studies 2 and 3 have smaller sample sizes, hence their precision is worse and the same -0.3 to -0.4 is estimated with zero within its confidence interval. Although the ‘significance’ is different between study 1 and studies 2 and 3, the actual findings are very similar. In fact, the ‘non-significant’ finding of study 3 has a larger effect size than the ‘significant’ one in study 1!
Here is the problem with vote counting. If you counted significance you would say ‘the evidence is inconsistent, with more studies failing to find an effect than studies finding one’. On the other hand, if you look at the actual parameter estimates, then the evidence is not remotely inconsistent: all studies concur that the effect is in the range of -0.3 or -0.4 standard deviations. And, surely, three independent estimates all in this narrow range ought to give you high confidence that the true effect is around here. You ought to have more confidence that there is an effect when you have added the evidence of studies 2 and 3 than you did when you just had study 1. But if you do vote-counting based on significance, then the opposite happens: your initial belief on the basis of ‘significant’ study 1 is eroded by the ‘non-significant’ studies 2 and 3.
There are even cases where none of the studies finds a significant effect, but the combined evidence suggests there is one. Imagine in our ibuprofen example if the forest plot had looked like this instead:
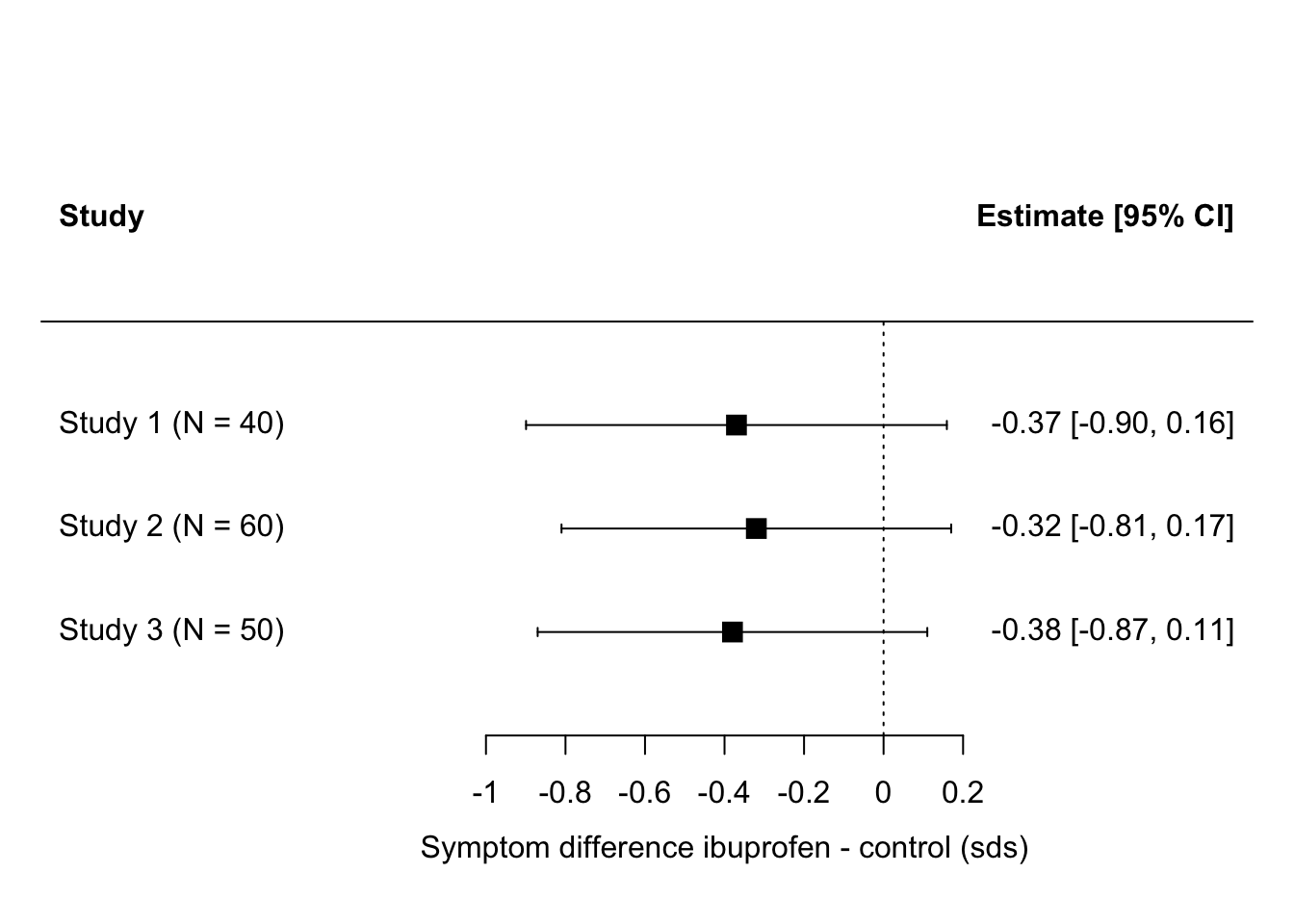
Here, none of the effects is ‘significant’ (i.e. not significantly different from zero) and so, in terms of vote counting, it’s a landslide for ‘no effect’. But, the studies are all pretty small. They all find parameter estimates in the -0.3 to -0.4 range, just with a broad confidence interval. We feel intuitively that the precision of the three studies considered together ought to be a lot better than any one of them considered individually. If we assume that our best estimate of the true effect size is somewhere close to the average of the estimates from the three studies, say around -0.34, and that the confidence interval for the three combined is smaller than for any one of the studies individually, then these three ‘non-significant’ studies actually seem to be telling us that there might be a significant effect.
Just as vote counting can make us believe there is no meaningful effect when there probably is one, it can make us believe there is a meaningful effect when there probably isn’t. Let’s imagine a case where there are a couple of very small studies finding large effects, and then one much more serious follow up finding en effect close to zero. It could look like this:
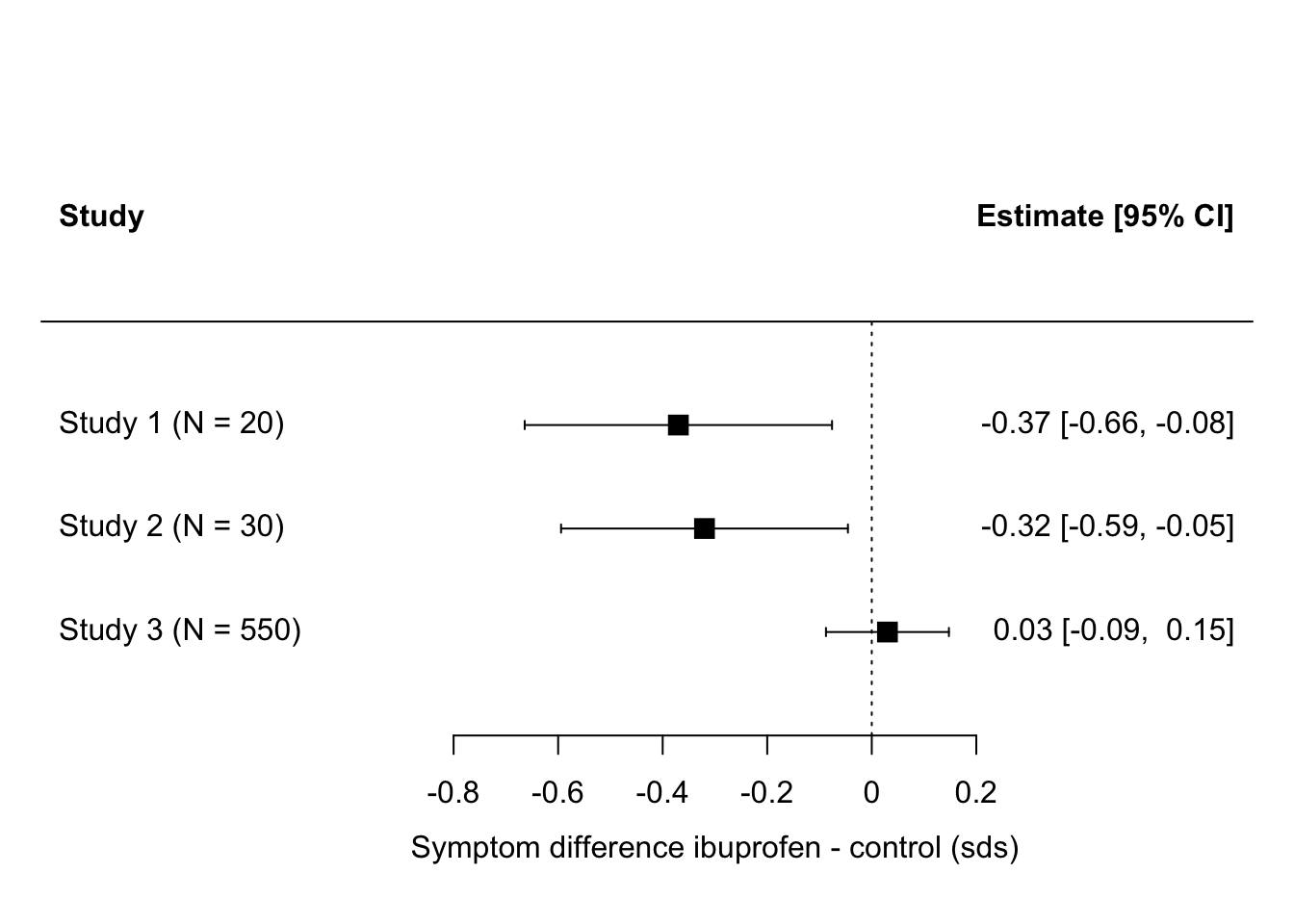
Here, two out of three had ‘significant’ effects, so vote-counting favours the hypothesis of an effect. But, if you consider the total number of people who have actually been studied, just 50 of them went into the studies claiming an effect, whereas 550 of them went into a study finding an effect size very close to zero. If the votes were weighted by the number of participants, and hence the amount of evidence, in the study, then study 3 would count a lot more than studies 1 and 2 combined.