3.1 Estimación por Máxima Verosimilitud (MLE)

La estimación por máxima verosimilitud es un método estadístico que busca encontrar los valores de los parámetros que hacen más probable haber observado los datos que tenemos.

3.1.1 Intuición básica

Imagina que tienes una bolsa con caramelos y quieres adivinar cuántos hay de cada color. Si sacas varios caramelos y ves que la mayoría son rojos, probablemente pienses que la bolsa tiene más caramelos rojos. Eso es máxima verosimilitud: elegir la suposición (valores de parámetros) que hace que los datos que vimos tengan la mayor probabilidad de ocurrir.

Visualizando la función de verosimilitud

# Simulamos datos de una normal con media 5 y sd 2
set.seed(123)
datos <- rnorm(30, mean = 5, sd = 2)

# Fijamos sigma para simplificar
sigma_fija <- 2

# Definimos la función de log-verosimilitud en función de mu
log_likelihood_mu <- function(mu) {
  n <- length(datos)
  ll <- -n * log(sigma_fija) - sum((datos - mu)^2) / (2 * sigma_fija^2)
  return(ll)
}

# Generamos valores de mu para graficar
mu_vals <- seq(3, 7, length.out = 200)
ll_vals <- sapply(mu_vals, log_likelihood_mu)

# Graficamos
plot(mu_vals, ll_vals, type = "l", lwd = 2, col = "blue",
     ylab = "Log-Verosimilitud", xlab = expression(mu),
     main = "Función de Verosimilitud en función de μ")
abline(v = mu_vals[which.max(ll_vals)], col = "red", lty = 2)
text(mu_vals[which.max(ll_vals)], max(ll_vals), 
     labels = paste0("Máximo en μ ≈ ", round(mu_vals[which.max(ll_vals)], 2)),
     pos = 4, col = "red")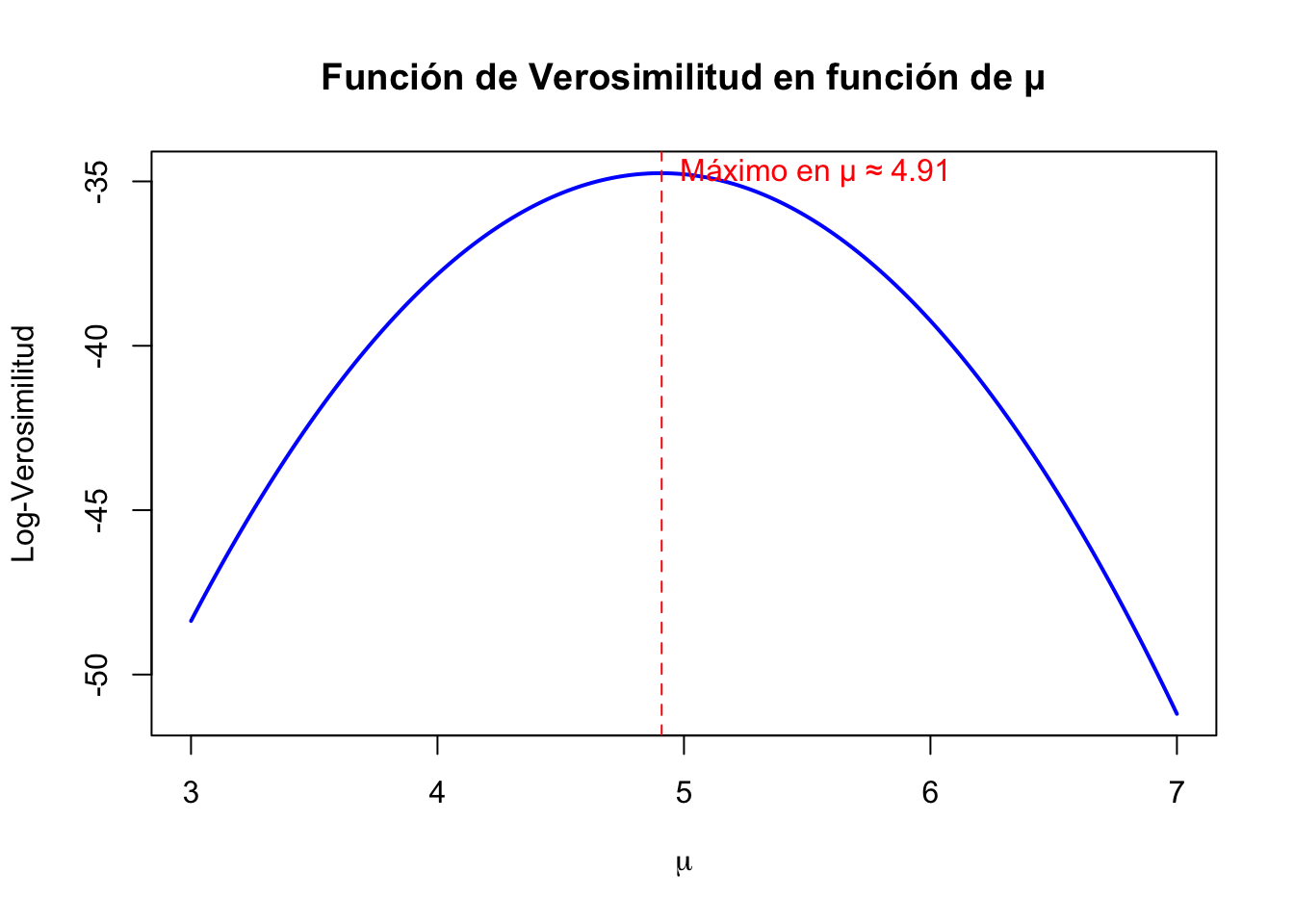

3.1.2 Ejemplo: Estimar media y desviación estándar con MLE

Supón que tienes una muestra de datos que crees que siguen una distribución normal, pero no conoces la media (\(\mu\)) ni la desviación estándar \(\sigma\)). La función de densidad para la normal es:

\[ f(x_i; \mu, \sigma) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{(x_i - \mu)^2}{2\sigma^2} \right) \]

Dado un conjunto de datos \(\{x_1, x_2, ..., x_n\}\), la función de verosimilitud es el producto de todas las probabilidades individuales:

\[ L(\mu, \sigma) = \prod_{i=1}^n f(x_i; \mu, \sigma) \]

Para simplificar, usamos el logaritmo de la verosimilitud (log-verosimilitud):

\[ \log L(\mu, \sigma) = -\frac{n}{2} \log(2\pi) - n \log(\sigma) - \frac{1}{2\sigma^2} \sum_{i=1}^n (x_i - \mu)^2 \]

El objetivo de MLE es encontrar los valores de \(\mu\) y \(\sigma\) que maximizan esta función.

En R

A continuación, generamos datos simulados y calculamos la estimación por máxima verosimilitud usando optimización.

# Simulamos datos de una normal con media 10 y desviación 2
set.seed(123)
x <- rnorm(100, mean = 10, sd = 2)

# Función negativa de log-verosimilitud (porque optim minimiza)
neg_log_likelihood <- function(par, data) {
  mu <- par[1]
  sigma <- par[2]
  
  # Penalización si sigma es negativa
  if (sigma <= 0) return(Inf)
  
  n <- length(data)
  logL <- -n * log(sigma) - sum((data - mu)^2) / (2 * sigma^2)
  return(-logL)  # Negativo para minimizar
}

# Estimación por MLE usando optim
mle_result <- optim(par = c(mean(x), sd(x)), 
                    fn = neg_log_likelihood, 
                    data = x,
                    method = "L-BFGS-B",
                    lower = c(-Inf, 0.0001))  # sigma > 0

mle_result$par  # mu y sigma estimados

## [1] 10.180812  1.816481