5.2 Ejemplo ilustrativo: estimación de \(\pi\)
set.seed(123)
n <- 10000
x <- runif(n)
y <- runif(n)
inside_circle <- (x^2 + y^2) <= 1
pi_estimate <- 4 * mean(inside_circle)
cat("Estimación de pi:", pi_estimate)## Estimación de pi: 3.18Este ejemplo usa el método de Monte Carlo para estimar el área de un círculo inscrito en un cuadrado (estimando así el valor de \(\pi\)).
Veamos el ejemplo paso a paso:
Paso 1: Definir las variables aleatorias
Se simulan puntos aleatorios \((x, y)\) dentro del cuadrado unidad \([0,1] \times [0,1]\). Cada punto es una variable aleatoria.
Paso 2: Asignar distribuciones de probabilidad
Las variables \(x\) e \(y\) se asumen distribuidas Uniforme(0,1), lo que garantiza una cobertura uniforme del cuadrado.
Paso 3: Generar múltiples escenarios
Se generan \(n = 10000\) simulaciones o escenarios aleatorios.
Paso 4: Calcular el resultado en cada escenario
Se calcula si cada punto cae dentro del cuarto de círculo de radio 1.
Paso 5: Analizar los resultados simulados
Se estima \(\pi\) como cuatro veces la proporción de puntos que caen dentro del círculo:
Este valor se aproxima al valor real de \(\pi \approx 3.1416\) usando simulación estadística.
set.seed(123)
n <- 10000
x <- runif(n)
y <- runif(n)
inside_circle <- (x^2 + y^2) <= 1
pi_estimate <- 4 * mean(inside_circle)
cat("Estimación de pi:", pi_estimate)## Estimación de pi: 3.18Este ejemplo usa el método de Monte Carlo para estimar el área de un círculo inscrito en un cuadrado (estimando así el valor de \(\pi\)).
5.2.1 Aplicación a Riesgos Cibernéticos
Supongamos que una organización desea estimar la pérdida financiera anual esperada por ataques cibernéticos exitosos.
Supuestos del modelo:
El número de ataques exitosos por año sigue una distribución Poisson(\(\lambda\) = 3).
La pérdida por ataque exitoso sigue una distribución lognormal(\(\mu\) = 10, \(\sigma\) = 1.5).
Se desean simular 10.000 años hipotéticos.
set.seed(123)
# Parámetros
n_sim <- 10000
lambda <- 3
mu <- 10
sigma <- 1.5
# Función de simulación por año
simular_perdida_anual <- function() {
n_ataques <- rpois(1, lambda)
if (n_ataques == 0) return(0)
sum(rlnorm(n_ataques, meanlog = mu, sdlog = sigma))
}
# Simulación Monte Carlo
perdidas <- replicate(n_sim, simular_perdida_anual())
# Estadísticas clave
mean(perdidas) # Pérdida esperada anual## [1] 200219.7## 95%
## 704838## 99%
## 1505755# Visualización
hist(perdidas, breaks = 50,
main = "Distribución simulada de pérdidas anuales por ciberataques",
xlab = "Pérdida anual (USD)", col = "steelblue", border = "white")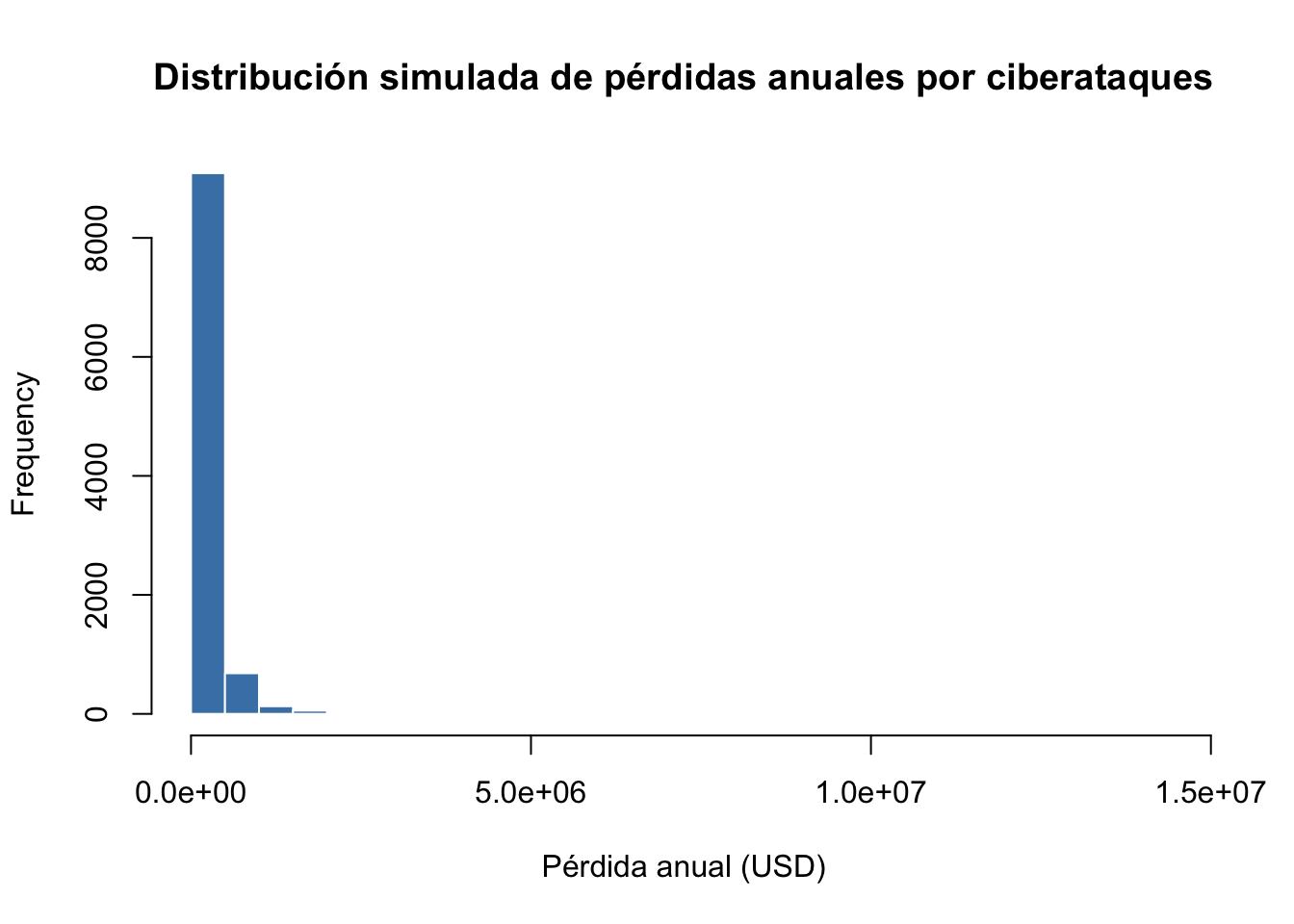
5.2.2 Relación con la Convolución
¿Qué es la convolución?
La convolución es una operación matemática que describe la distribución de la suma de dos variables aleatorias independientes. Si \(X \sim f(x)\) y \(Y \sim g(y)\), entonces la suma \(Z = X + Y\) tiene distribución dada por:
\[ (f * g)(z) = \int_{-\infty}^{\infty} f(x)g(z - x) \, dx \]
5.2.3 Convolución en riesgo cibernético
Cuando el número de eventos \(N\) también es aleatorio, como en una distribución Poisson, la pérdida total \(S = \sum_{i=1}^N X_i\) no puede modelarse con una sola convolución. En cambio, se utiliza una mezcla ponderada de convoluciones:
\[ f_S(s) = \sum_{n=0}^{\infty} \mathbb{P}(N = n) \cdot f^{*n}(s) \]
Donde:
- \(\mathbb{P}(N = n)\) es la probabilidad de que ocurran exactamente \(n\) eventos.
- \(f^{*n}(s)\) representa la n-ésima convolución de la densidad \(f\), es decir, la densidad de la suma de \(n\) pérdidas independientes.
¿Qué significa \(f^{*n}(s)\)?
La notación \(f^{*n}(s)\) representa la convolución de \(n\) funciones de densidad. Para \(n = 2\), por ejemplo:
\[ f^{*2}(s) = \int_{0}^{s} f(x) f(s - x) \, dx \]
Esto es la densidad de \(X_1 + X_2\) si \(X_1, X_2 \sim f(x)\) son independientes.
Si \(f(x)\) es, por ejemplo, una distribución exponencial \(\text{Exp}(\lambda)\), entonces la convolución tiene forma cerrada:
\[ f^{*2}(s) = \lambda^2 s e^{-\lambda s}, \quad s \geq 0 \]
corresponde a una distribución Gamma(2, \(\lambda\)).
Para \(n > 2\):
Se vuelve más complicado. Por ejemplo, para \(n = 3\):
\[ f^{*3}(s) = \int_{-\infty}^{\infty} f^{*2}(x) f(s - x) \, dx \]
Y así sucesivamente, lo cual rápidamente se vuelve intratable analíticamente, especialmente si \(f\) es lognormal o Burr.
Relación con la simulación Monte Carlo
En vez de resolver esta expresión analíticamente, Monte Carlo genera directamente muestras desde el modelo generativo. Formalmente, se estima:
- Para cada simulación \(k\):
- Simular \(N^{(k)} \sim \text{Poisson}(\lambda)\)
- Simular \(X_1^{(k)}, \dots, X_{N^{(k)}}^{(k)} \sim f(x)\)
- Calcular \(S^{(k)} = \sum_{i=1}^{N^{(k)}} X_i^{(k)}\)
- Repetir para \(k = 1, \dots, M\) veces
Entonces:
\[ \{ S^{(1)}, S^{(2)}, \dots, S^{(M)} \} \approx \text{muestra de la distribución de } S \]
Y se pueden estimar:
- \(\mathbb{E}[S] \approx \frac{1}{M} \sum_{k=1}^{M} S^{(k)}\)
- VaR, percentiles, colas extremas, etc.
| Elemento | Expresión teórica | Aproximación Monte Carlo |
|---|---|---|
| Distribución de pérdidas | \(f_S(s) = \sum_{n=0}^{\infty} P(N=n) \cdot f^{*n}(s)\) | Muestreo empírico de \(S^{(k)} = \sum X_i\) |
| Complejidad | Altamente compleja, sin forma cerrada | Simple de implementar |
| Ejemplo | Poisson + Lognormal | rpois() + rlnorm() |
5.2.4 Monte Carlo como aproximación
Realizar esta convolución de forma analítica es complejo. Por eso, usamos simulación de Monte Carlo para aproximar la distribución de \(S\):
- Simulamos un valor de \(N\).
- Generamos \(N\) pérdidas individuales \(X_i\).
- Calculamos la suma total \(S\).
- Repetimos este proceso muchas veces para obtener una aproximación empírica de la distribución.
Este enfoque permite obtener estimaciones del valor esperado, VaR, colas de riesgo, etc., sin necesidad de derivar convoluciones analíticas.