2.5 Ejercicios

2.5.1 Normal y log-normal

Ejercicio 1: Densidad de una pérdida puntual (Normal)

Una base de datos de eventos muestra que las pérdidas siguen una distribución normal con media $20,000 y desviación estándar $5,000.

¿Cuál es la densidad de probabilidad para una pérdida puntual de $25,000?

## [1] 4.839414e-05

Ejercicio 2: Probabilidad de que la pérdida supere los $30,000

## [1] 0.02275013

Ejercicio 3: VaR al 99% (percentil crítico)

Calcular el valor en riesgo (VaR) al 99%.

## [1] 31631.74

Ejercicio 4: Gráfico de densidad con valores críticos

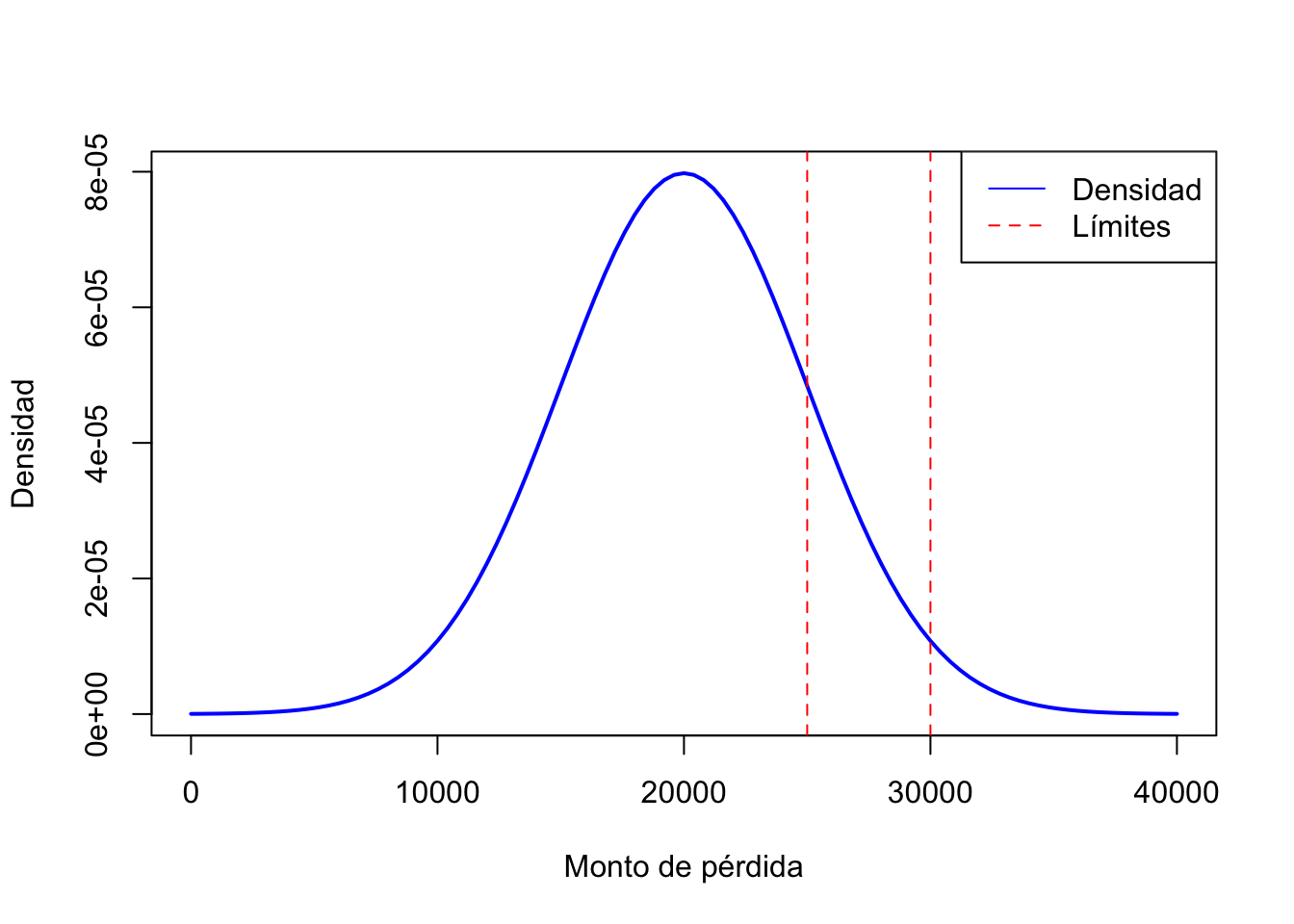
Ejercicio 5: Probabilidad de pérdida severa (Lognormal)

Se asume que las pérdidas siguen una distribución lognormal con media logarítmica 9.5 y desviación estándar logarítmica 0.8.

Calcular la probabilidad de que la pérdida supere $20,000.

## [1] 0.3070044

Ejercicio 6: Percentil 95% (VaR lognormal)

## [1] 49805.61

Ejercicio 7: Comparación visual Normal vs Lognormal

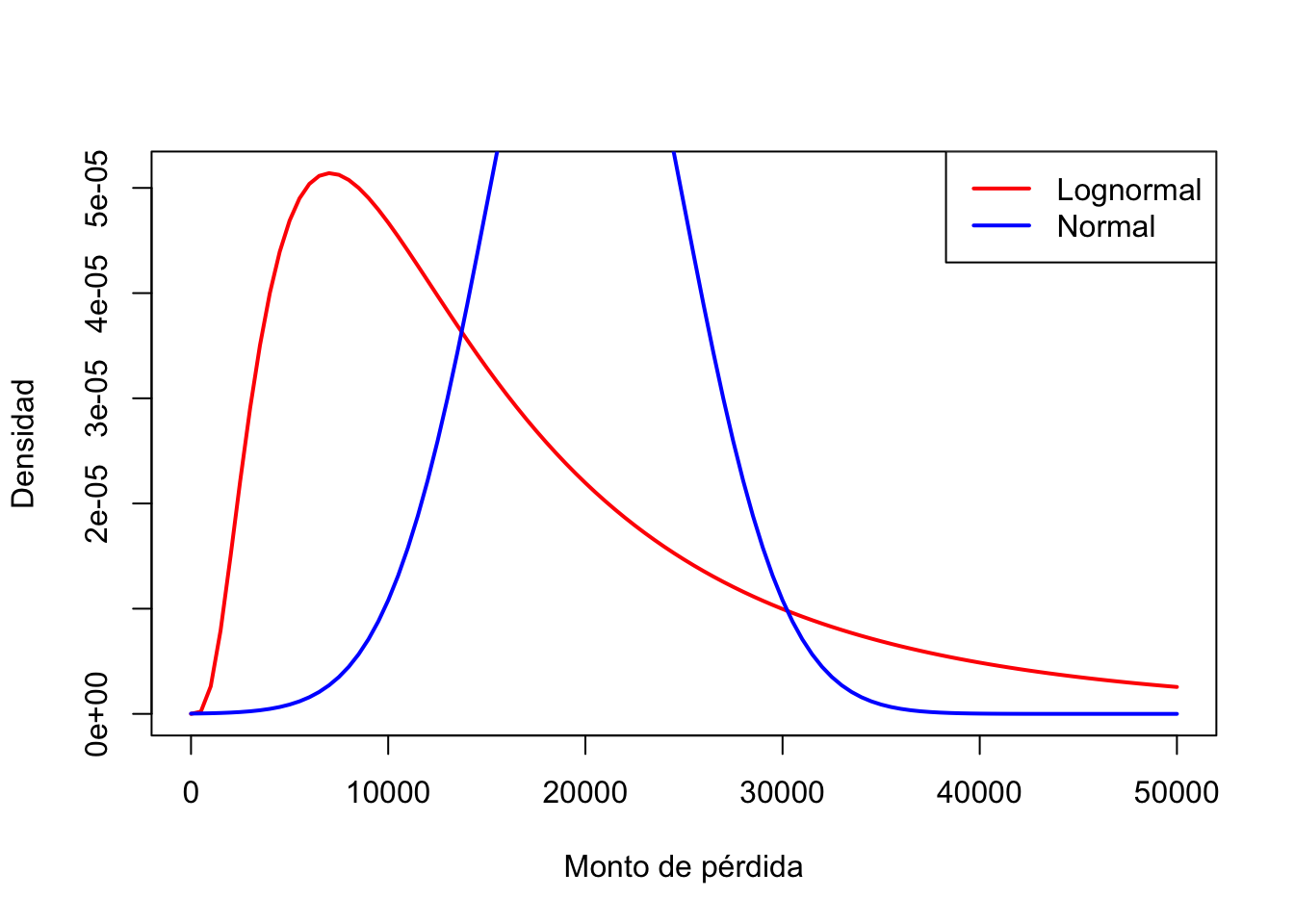
Ejercicio 8: Simulación de pérdidas

## [1] 20080.64

##      95% 
## 28380.67

## [1] 19133.01

##      95% 
## 48236.28

Ejercicio 9: Probabilidad de pérdida extrema

¿Cuál es la probabilidad de una pérdida mayor a $100,000 bajo la lognormal?

## [1] 0.005932119

Ejercicio 10: Umbral de alerta automática

¿Cuál es el umbral que activa una alerta si se supera el percentil 97.5%?

## [1] "Alerta: activar si pérdida > $ 64085.36"

2.5.2 Normal estándar y t

Ejercicio 1: Probabilidad bajo la distribución normal estándar

Un indicador de pérdida ha sido estandarizado y su valor es Z = 1.65.
Esto proviene de una variable con media 0 y desviación estándar 1.
¿Cuál es la probabilidad de observar un valor menor a ese?

## [1] 0.9505285

¿Y cuál es la probabilidad de observar un valor mayor a ese?

## [1] 0.04947147

Ejercicio 2: Comparación de colas: normal vs t de Student

Supón que estandarizaste una estadística de pérdida severa y obtuviste un valor de 2 desviaciones estándar.
Calcular la probabilidad de exceder este valor:

• Bajo la distribución normal estándar
• Bajo la distribución t con 5 grados de libertad

## [1] 0.02275013

## [1] 0.05096974

Reflexión: ¿Cuál tiene mayor probabilidad en la cola? ¿Qué implica esto para estimaciones con muestras pequeñas?

Ejercicio 3: VaR al 97.5% con varianza estimada (cuantil t)

Se desea calcular el valor crítico del percentil 97.5% para una variable que proviene de una muestra de tamaño 10 (df = 9).

• Usando la distribución t:

## [1] 2.262157

• Comparado con la normal estándar:

qnorm(0.975)

## [1] 1.959964

Ejercicio 4: Probabilidad entre dos valores

Supón que tienes una variable estandarizada y deseas calcular la probabilidad de que esté entre -1.5 y 1.5.
Esto se puede calcular como:

## [1] 0.8663856

¿Qué interpretación tiene este resultado en el contexto del análisis de riesgos?

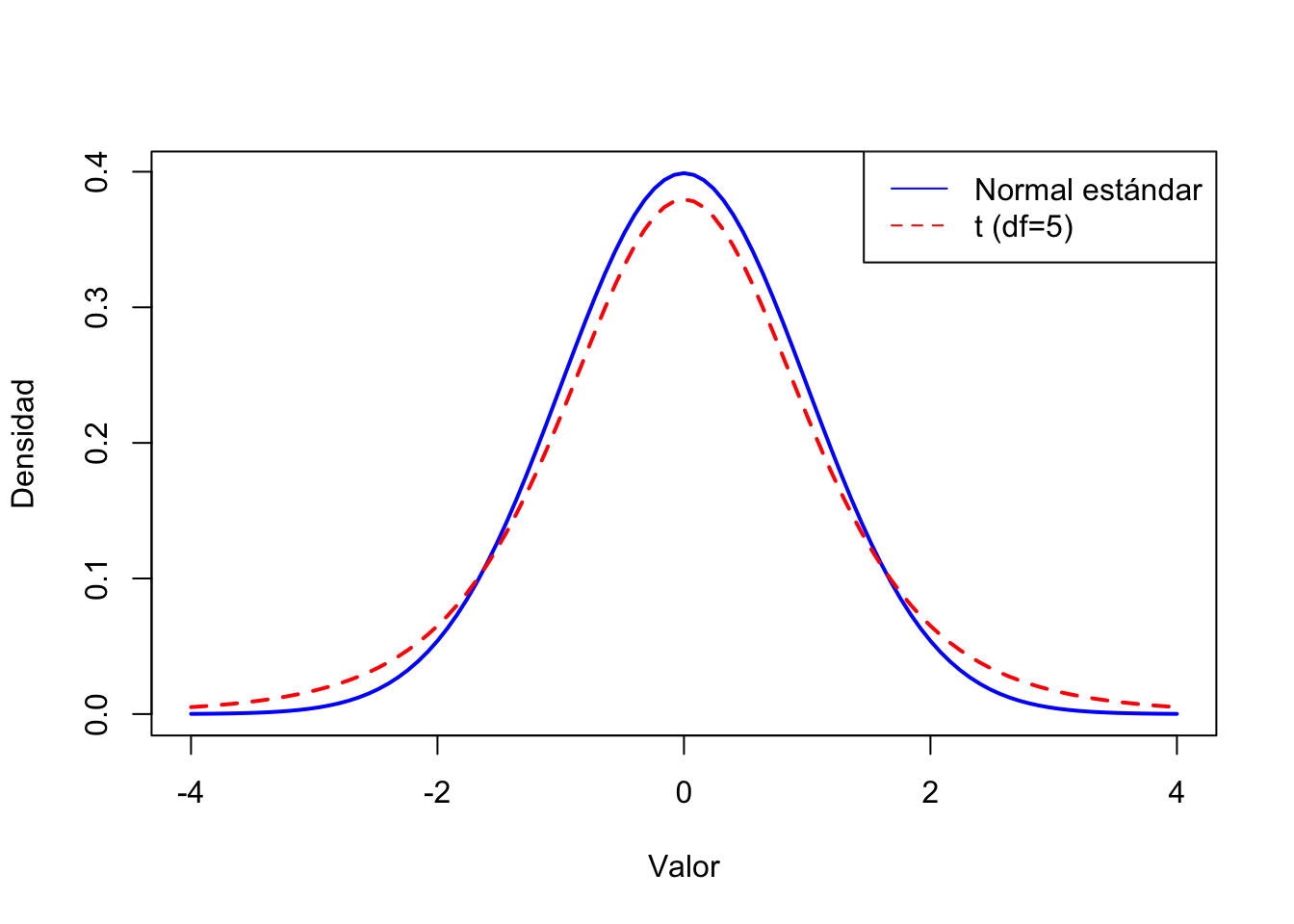
Ejercicio 5: Gráfico comparativo de densidades

Comparar visualmente la distribución normal estándar con una t de Student con 5 grados de libertad: