2.3 Correlación
Se aborda a continuación medidas de correlación paramétricas y no paramétricas. El coeficiente de correlación es una medida de asociación que varía entre -1 y 1.
2.3.1 Correlación de Pearson
El coeficiente de correlación empírico es:
\[ r = \frac{\sum (x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum (x_i-\bar{x})^2\sum (y_i-\bar{y})^2}} \]
La función cor en R calcula la correlación entre dos o más vectores.
uu = "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/company_sales_data.csv"
datos <- read.csv(uu)
cor(datos$moisturizer,datos$toothpaste)## [1] 0.6423698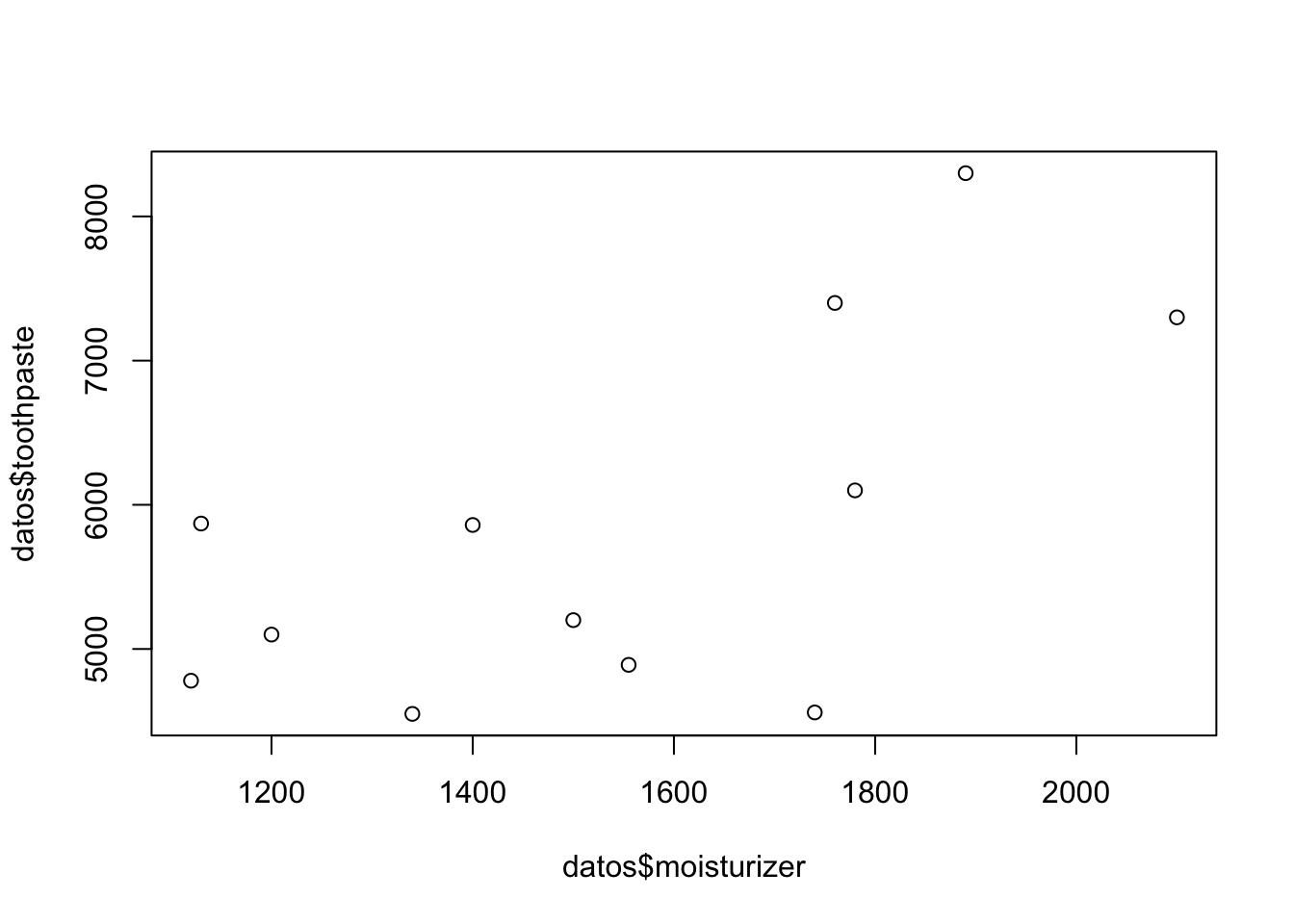
Las funciones elementales en R requieren que el usuario especifique la acción a tomar con los NA. En el caso de la correlación:
## [1] 0.6423698Se pude obtener todas las correlaciones de un data frame:
## month_number facecream facewash toothpaste bathingsoap shampoo
## month_number 1.00000000 0.042267493 0.66092197 0.76319018 0.7059640 0.11204252
## facecream 0.04226749 1.000000000 -0.21134758 -0.28483136 -0.2435129 -0.24358628
## facewash 0.66092197 -0.211347581 1.00000000 0.64236980 0.5307611 -0.03320443
## toothpaste 0.76319018 -0.284831364 0.64236980 1.00000000 0.6894477 0.04842363
## bathingsoap 0.70596401 -0.243512937 0.53076109 0.68944765 1.0000000 0.13756757
## shampoo 0.11204252 -0.243586279 -0.03320443 0.04842363 0.1375676 1.00000000
## moisturizer 0.66092197 -0.211347581 1.00000000 0.64236980 0.5307611 -0.03320443
## total_units 0.70933492 -0.006309553 0.41259966 0.53497851 0.7452802 0.29747168
## total_profit 0.70933492 -0.006309553 0.41259966 0.53497851 0.7452802 0.29747168
## moisturizer total_units total_profit
## month_number 0.66092197 0.709334918 0.709334918
## facecream -0.21134758 -0.006309553 -0.006309553
## facewash 1.00000000 0.412599658 0.412599658
## toothpaste 0.64236980 0.534978513 0.534978513
## bathingsoap 0.53076109 0.745280238 0.745280238
## shampoo -0.03320443 0.297471682 0.297471682
## moisturizer 1.00000000 0.412599658 0.412599658
## total_units 0.41259966 1.000000000 1.000000000
## total_profit 0.41259966 1.000000000 1.000000000Sin embargo, los cálculos que hemos hecho, no nos indican si la correlación es significativamente diferente de cero. Para ello hacemos:
##
## Pearson's product-moment correlation
##
## data: datos$moisturizer and datos$toothpaste
## t = 2.6505, df = 10, p-value = 0.02429
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.1084485 0.8886605
## sample estimates:
## cor
## 0.64236982.3.2 Correlación de Spearman \(\rho\)
Esta se obtiene al reemplazar las observaciones por su rango y luego se calcula la correlación. La hipótesis nula es la independencia entre las variables.
##
## Spearman's rank correlation rho
##
## data: datos$moisturizer and datos$toothpaste
## S = 112, p-value = 0.04
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
## rho
## 0.6083916Interpretación de la correlación:
- La correlación esta siempre entre -1 y 1. Lo primero que se interpreta es el signo
- Directamente proporcional si es positivo, si es negativo pasa lo contrario
- En segundo lugar se interpreta es la fuerza de la relación. Si esta más cerca de 1, significa que si aumenta una variable, la otra también.
- Números intermedios, reducen la fuerza de la relación.
2.3.3 Bivariado
Veamos un scatterplot más informativo a partir de la tabla 2.8:
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/refs/heads/master/GA/table2_8.csv"
datos <- read.csv(uu, sep=";", header=TRUE)
scatterplot(datos$TOTALEXP, datos$FOODEXP, smooth=F, main="Relación entre el gasto total y gasto en comida",xlab="Gasto total", ylab="Gasto en comida",grid=F)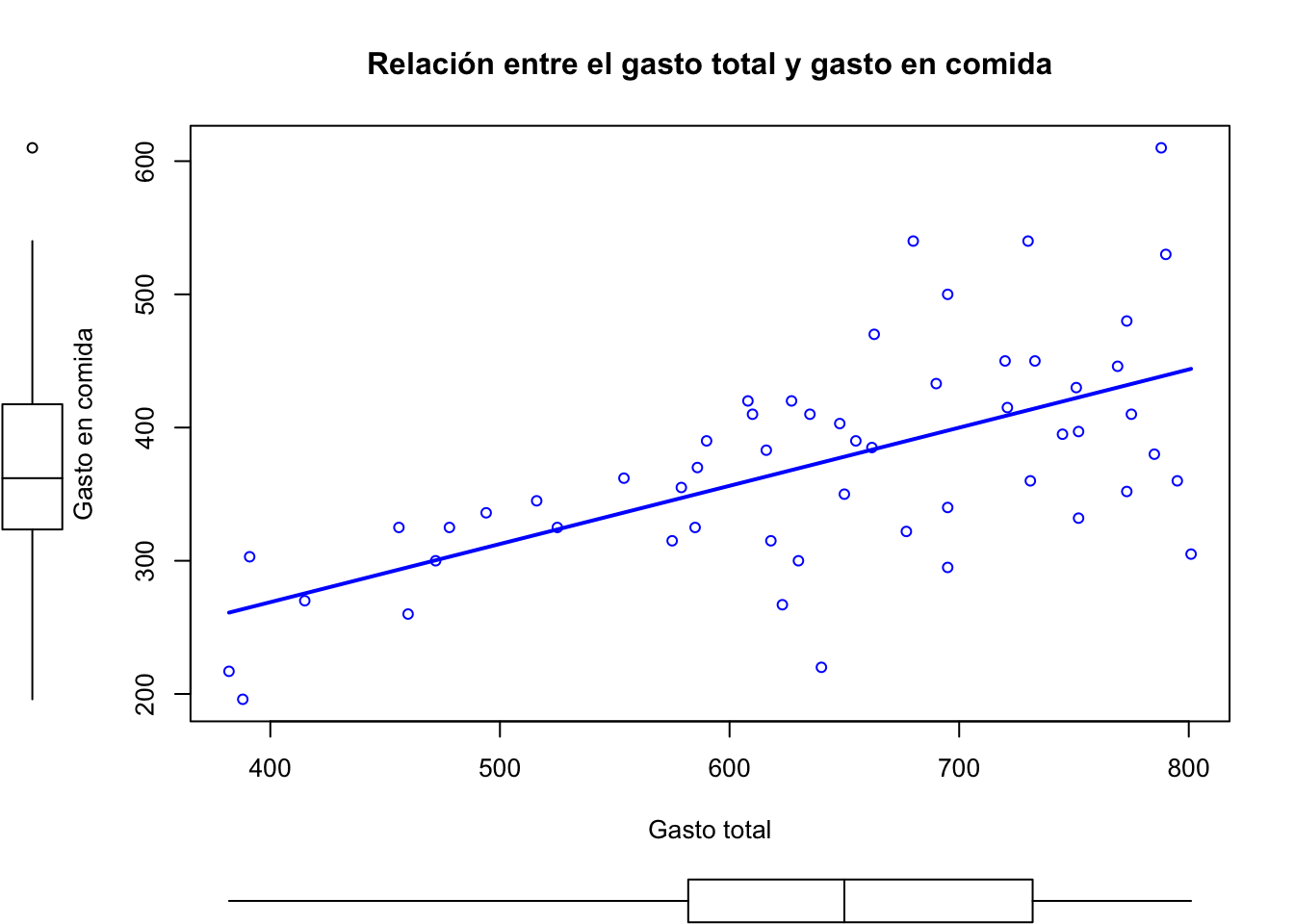
La normalización de datos se lo puede realizar de varias formas, podemos entrar a la ayuda de esta función para más detalle. La estandarización más usada es n1, es decir: (observación-media)/desviación estándar
# install.packages("clusterSim")
normfood <- data.Normalization (datos$FOODEXP,type="n1")
normtot <- data.Normalization (datos$TOTALEXP,type="n1")¿Qué ganamos normalizando los datos?
## [1] 7.266914e-17## [1] 1Veamos los resultados gráficamente:
plot(normtot, normfood, main="Relación entre el gasto total y gasto en comida (estandarizadas)",xlab="Gasto total", ylab="Gasto en comida")
abline(v=0)
abline(h=0)
Interpretación
- Cuadrante 1: gasto total y en comida en comida mayor que el promedio
- Cuadrante 2: gasto total inferior al promedio, pero gastan más que el promedio en comida
- Cuadrante 3: tienen menos gasto total que el promedio y el gasto en comida es menor al promedio
- Cuadrante 4: tiene un gasto total mayor el promedio pero su gasto en comida es menor al promedio
Veamos algunas particularidades de las funciones estadísticas básicas:
## [1] 13493.04## [1] 0.6081313## [1] 1## [1] 0.6081313Ahora veamos:
## [1] 0.6081313Conclusión:La correlación no depende de las unidades en las que estámos midiendo, ¿La varianza?
Una última conclusión:
## [1] 19.97591## [1] 15.97591## [1] 0.6081313Conclusión: La correlación no depende ni de la escala ni del origen