2.2 Estadística inferencial: Intervalos de confianza y pruebas de hipótesis en gestión de riesgos.

2.2.1 ¿Qué es un Intervalo de Confianza?

Un intervalo de confianza (IC) es un rango de valores que se calcula a partir de una muestra de datos y que probablemente contiene el valor verdadero de un parámetro poblacional. Se expresa como:

\[ IC = \bar{x} \pm z_{\alpha/2} \cdot \frac{s}{\sqrt{n}} \]

o, si se desconoce la varianza poblacional, con distribución t:

\[ IC = \bar{x} \pm t_{\alpha/2, df} \cdot \frac{s}{\sqrt{n}} \]

2.2.2 Aplicación en Riesgos

Los IC son útiles para:

Estimar rangos de pérdidas operativas esperadas
Evaluar proporciones de fallas tecnológicas
Estimar márgenes de error para indicadores de ciberseguridad
Respaldar decisiones con fundamentos estadísticos

2.2.3 Elementos del Intervalo de Confianza

Nivel de confianza: 90%, 95%, 99%
Estadístico crítico: z o t
Error estándar: variabilidad de la estimación
Tamaño muestral: cuanto mayor, más preciso el intervalo

2.2.4 Ejemplo: Intervalo para la media de pérdidas

set.seed(123)
perdidas <- rlnorm(50, meanlog = 9, sdlog = 0.5)
media <- mean(perdidas)
error <- sd(perdidas) / sqrt(length(perdidas))
t_crit <- qt(0.975, df = length(perdidas) - 1)
ic_media <- c(media - t_crit * error, media + t_crit * error)
ic_media

## [1]  7892.207 10453.564

2.2.5 Ejemplo: Proporción de eventos tecnológicos con impacto alto

eventos <- c(rep(1, 18), rep(0, 32))  # 1 = impacto alto
prop <- mean(eventos)
n <- length(eventos)
z <- qnorm(0.975)
se <- sqrt(prop * (1 - prop) / n)
ic_prop <- c(prop - z * se, prop + z * se)
ic_prop

## [1] 0.2269532 0.4930468

2.2.6 Visualización del intervalo de confianza para la media

library(ggplot2)
df <- data.frame(
  media = media,
  inf = ic_media[1],
  sup = ic_media[2]
)

ggplot(df) +
  geom_point(aes(x = 1, y = media), size = 3) +
  geom_errorbar(aes(x = 1, ymin = inf, ymax = sup), width = 0.1) +
  labs(title = "Intervalo de confianza para pérdida promedio", y = "Pérdida") +
  theme_minimal()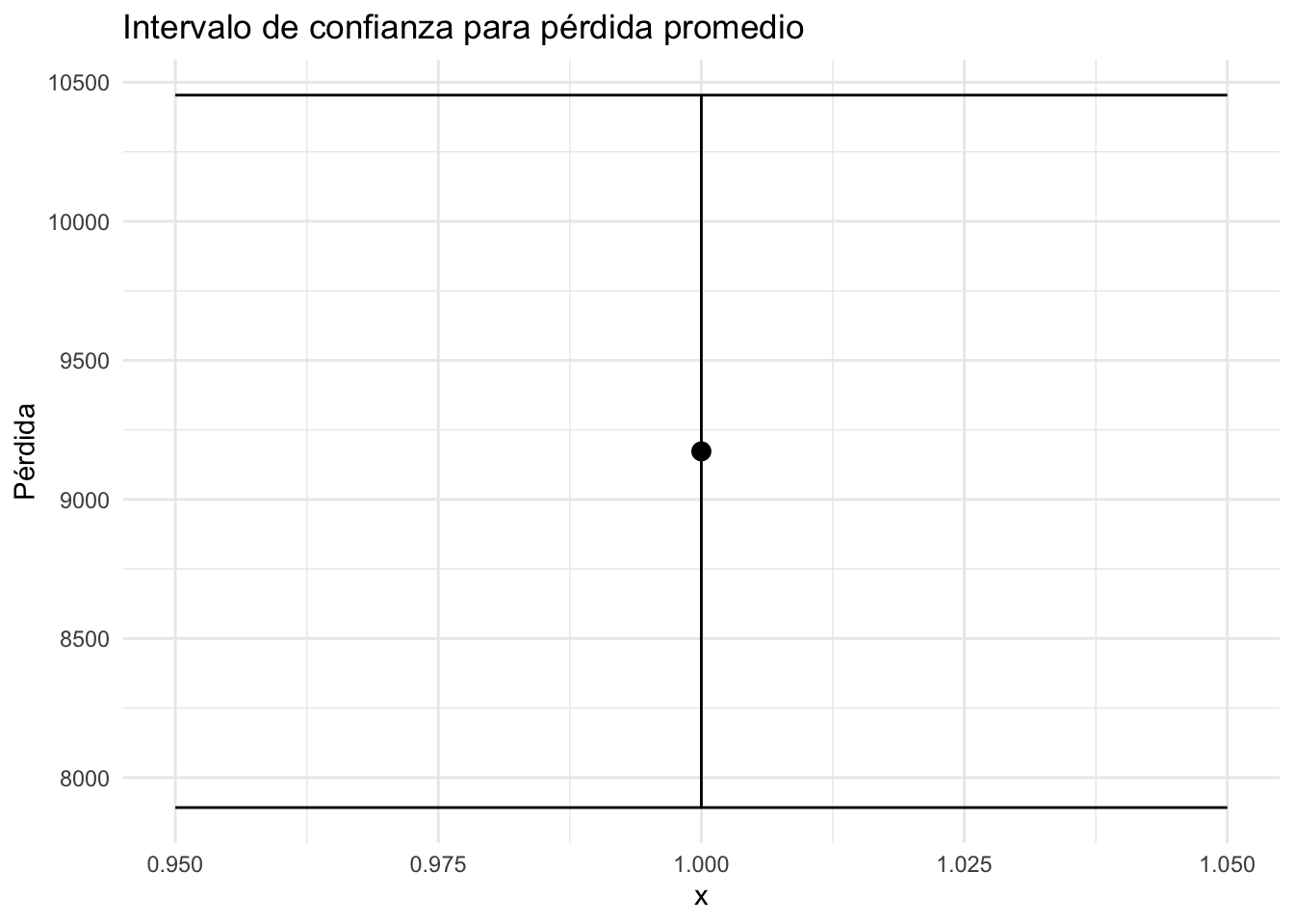

2.2.7 Extensiones

Intervalos para VaR (Valor en Riesgo)
Intervalos por bootstrap

2.2.8 Práctica

2.2.8.1 Estimar IC para media de pérdidas por phishing

set.seed(42)
phishing_losses <- rlnorm(40, meanlog = 8.5, sdlog = 0.7)
mean_p <- mean(phishing_losses)
se_p <- sd(phishing_losses) / sqrt(length(phishing_losses))
tval <- qt(0.975, df = length(phishing_losses) - 1)
ic_phishing <- c(mean_p - tval * se_p, mean_p + tval * se_p)
ic_phishing

## [1] 4863.935 8365.124

2.2.8.2 IC para proporción de eventos tecnológicos detectados a tiempo

eventos_detectados <- c(rep(1, 28), rep(0, 12))  # 1 = detectado a tiempo
prop_d <- mean(eventos_detectados)
n_d <- length(eventos_detectados)
se_d <- sqrt(prop_d * (1 - prop_d) / n_d)
ic_detect <- c(prop_d - z * se_d, prop_d + z * se_d)
ic_detect

## [1] 0.5579871 0.8420129

2.2.8.3 IC para VaR estimado por simulación Monte Carlo

set.seed(99)
sim_perdidas <- rlnorm(1000, meanlog = 9.1, sdlog = 0.6)
VaRs <- replicate(500, quantile(sample(sim_perdidas, 500, replace = TRUE), 0.95))
mean_VaR <- mean(VaRs)
se_VaR <- sd(VaRs) / sqrt(length(VaRs))
ic_VaR <- c(mean_VaR - z * se_VaR, mean_VaR + z * se_VaR)
ic_VaR

## [1] 24181.76 24432.57

2.2.9 Pruebas de hipótesis

En toda prueba de hipótesis, implícita o explícitamente se cubren los siguientes puntos:

2.2.9.1 Planteamiento de las hipótesis

Hipótesis nula (\(H_0\)): Afirmación que se quiere poner a prueba; generalmente representa la ausencia de efecto, diferencia o relación.
Hipótesis alternativa (\(H_1\) o \(H_a\)): Afirmación que se aceptaría si se rechaza \(H_0\); representa la existencia de un efecto, diferencia o relación.

2.2.9.2 Elección del nivel de significancia (\(\alpha\))

Es la probabilidad máxima de cometer un error tipo I (rechazar \(H_0\) cuando es verdadera).
Comúnmente se usa \(\alpha = 0.05\), aunque puede variar según el contexto (por ejemplo, \(\alpha = 0.01\) en estudios médicos).

2.2.9.3 Selección del estadístico de prueba

Depende del tipo de variable y del contraste planteado:

\(t\)-student para medias (cuando la varianza poblacional es desconocida).
\(z\) para proporciones o medias (cuando la varianza es conocida).
\(\chi^2\) para variables categóricas (pruebas de independencia o bondad de ajuste).
\(F\) para comparar varianzas o modelos (ANOVA, regresión).

2.2.9.4 Distribución del estadístico bajo \(H_0\)

Determina cómo se comporta el estadístico si la hipótesis nula es verdadera.
Se utiliza para obtener el valor crítico o el p-valor.

2.2.9.5 Criterio de decisión

Valor crítico: Se compara el estadístico con un umbral derivado de la distribución teórica.
P-valor: Probabilidad de obtener un resultado tan extremo como el observado, bajo \(H_0\).
- Si \(\text{p-valor} < \alpha\), se rechaza \(H_0\).
- Si \(\text{p-valor} \geq \alpha\), no se rechaza \(H_0\).

2.2.9.6 Conclusión

La conclusión debe estar formulada en el contexto del problema.
Nunca se dice que \(H_0\) es “verdadera”, sino que no hay suficiente evidencia para rechazarla.

2.2.10 Errores posibles

Error tipo I (\(\alpha\)): Rechazar \(H_0\) siendo verdadera.
Error tipo II (\(\beta\)): No rechazar \(H_0\) siendo falsa.
Poder de la prueba: \(1 - \beta\), probabilidad de detectar un efecto si realmente existe.

Matriz de confusión adaptada a pruebas de hipótesis

	Realidad: \(H_0\) verdadera	Realidad: \(H_0\) falsa
Decisión: No rechazar \(H_0\)	Verdadero negativo (decisión correcta)	Error tipo II (falso negativo)
Decisión: Rechazar \(H_0\)	Error tipo I (falso positivo)	Verdadero positivo (decisión correcta)

Interpretación de cada celda

Término	Significado
Error tipo I	Rechazar \(H_0\) cuando en realidad es cierta.
Error tipo II	No rechazar \(H_0\) cuando en realidad es falsa.
Verdadero negativo	Decidir no rechazar \(H_0\) y que efectivamente \(H_0\) sea verdadera.
Verdadero positivo	Rechazar \(H_0\) y que efectivamente \(H_0\) sea falsa.

2.2.11 Test sobre una y dos muestras

Se introducen dos funciones: t.test y wilcox.test para el test t y el test de Wilcoxon respectivamente. Ambos pueden ser usados para una muestra o dos muestras así como para datos pareados. Note que el test de Wilcoxon para dos muestras es lo mismo que el test de Mann–Whitney.

2.2.11.1 El test t

Este test se basa en el supuesto de normalidad de los datos. Es decir que los datos \(x_1 \ldots, x_n\) se asumen como realizaciones independientes de variables aleatorias con media \(\mu\) y media \(\sigma^2\), \(N(\mu,\sigma^2)\). Se tiene que la hipótesis nula es que \(\mu = \mu_0\).

Se puede estimar los parámetros \(\mu\) y \(\sigma\) por la media \(\bar{x}\) y la desviación estándar \(\sigma\), aunque recuerde que solo son estimaciones del valor real.

Veamos un ejemplo del consumo diario de calorías de \(11\) mujeres:

daily.intake <- c(5260,5470,5640,6180,6390,6515,
                  6805,7515,7515,8230,8770)

Veamos algunas estadísticas de resumen:

mean(daily.intake)

## [1] 6753.636

sd(daily.intake)

## [1] 1142.123

quantile(daily.intake)

##   0%  25%  50%  75% 100% 
## 5260 5910 6515 7515 8770

Se podría querer saber si el consumo de energía de las mujeres se desvía de una valor recomendado de \(7725\). Asumiendo que los datos vienen de una distribución normal, el objetivo es hacer una prueba para saber si la media de la distribución es \(\mu = 7725\).

t.test(daily.intake,mu=7725)

## 
##  One Sample t-test
## 
## data:  daily.intake
## t = -2.8208, df = 10, p-value = 0.01814
## alternative hypothesis: true mean is not equal to 7725
## 95 percent confidence interval:
##  5986.348 7520.925
## sample estimates:
## mean of x 
##  6753.636

Analicemos el resultado como Jack el Destripador (por partes).

One Sample t-test: Muestra el tipo de test.
data: daily.intake: Indica los datos usados para el test
t = -2.8208, df = 10, p-value = 0.01814: Aquí se empieza a poner interesante. Arroja el valor del estadístico t, los grados de libertad y el valor p. Como tenemos el valor p, no es necesario ir a la tabla de valores de la distribución t. Con un nivel de significancia de \(5\%\), en este caso se rechaza la hipótesis nula.
alternative hypothesis: true mean is not equal to 7725. Esto contiene dos pedazos de información importante: + El valor puntual sobre el que realizamos el test. + Que el test es de dos colas (not equal to).
95 percent confidence interval: es el intervalo de confianza de la media verdadera.
sample estimates: es la estimación puntual de la media verdadera.

2.2.11.2 Prueba de los rangos con signo de Wilcoxon

Si se desea evitar el supuesto de normalidad de los datos, los métodos de distribución libre son una alternativa. Estos generalmente se obtienen reemplazando los datos con estadísticos de orden.

wilcox.test(daily.intake, mu=7725)

## Warning in wilcox.test.default(daily.intake, mu = 7725): cannot compute exact p-value with
## ties

## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  daily.intake
## V = 8, p-value = 0.0293
## alternative hypothesis: true location is not equal to 7725

Se ve que no se tiene tantos resultados como en el test t. Esto es porque no se tiene la estimación de un parámetro por lo que no hay intervalos de confianza, etc. Para efectos prácticos, cuando se trata de una muestra, el test t y el de Wilcoxon suelen arrojar resultados muy similares.

2.2.11.3 Test t para dos muestras

Se usa esta prueba con la hipótesis nula de que dos muestras provengan de distribuciones normales con la misma media.

Se puede tener dos enfoques, que las muestras tengan la misma varianza (enfoque clásico) o difieran en varianza.

uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/refs/heads/master/energy.csv"
energy <- read.csv(uu)
t.test(energy$expend~energy$stature)

## 
##  Welch Two Sample t-test
## 
## data:  energy$expend by energy$stature
## t = -3.8555, df = 15.919, p-value = 0.001411
## alternative hypothesis: true difference in means between group lean and group obese is not equal to 0
## 95 percent confidence interval:
##  -3.459167 -1.004081
## sample estimates:
##  mean in group lean mean in group obese 
##            8.066154           10.297778

El intervalo de confianza es para las diferencias entre las medias (note que no contiene a 0). Por defecto se calcula el test asumiendo que se tiene varianzas diferentes en las muestras. Si se desea especificar que las varianzas con iguales se tiene:

t.test(energy$expend~energy$stature, var.equal=T)

## 
##  Two Sample t-test
## 
## data:  energy$expend by energy$stature
## t = -3.9456, df = 20, p-value = 0.000799
## alternative hypothesis: true difference in means between group lean and group obese is not equal to 0
## 95 percent confidence interval:
##  -3.411451 -1.051796
## sample estimates:
##  mean in group lean mean in group obese 
##            8.066154           10.297778

Note que ahora los grados de libertad ahora son \(13+9-2 = 20\)

2.2.11.4 Comparación de varianzas

Aún cuando en R se puede hacer la prueba sobre dos muestras sin el supuesto de igualdad en las varianzas, podrías estar interesado en hacer una prueba exclusiva de este supuesto.

var.test(energy$expend~energy$stature)

## 
##  F test to compare two variances
## 
## data:  energy$expend by energy$stature
## F = 0.78445, num df = 12, denom df = 8, p-value = 0.6797
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  0.1867876 2.7547991
## sample estimates:
## ratio of variances 
##           0.784446

Note que este test asume que los grupos son independientes, no se debe aplicar el test cuando los datos son dependientes.

2.2.11.5 Test de Wilcoxon para dos muestras.

wilcox.test(energy$expend~energy$stature)

## Warning in wilcox.test.default(x = DATA[[1L]], y = DATA[[2L]], ...): cannot compute exact
## p-value with ties

## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  energy$expend by energy$stature
## W = 12, p-value = 0.002122
## alternative hypothesis: true location shift is not equal to 0