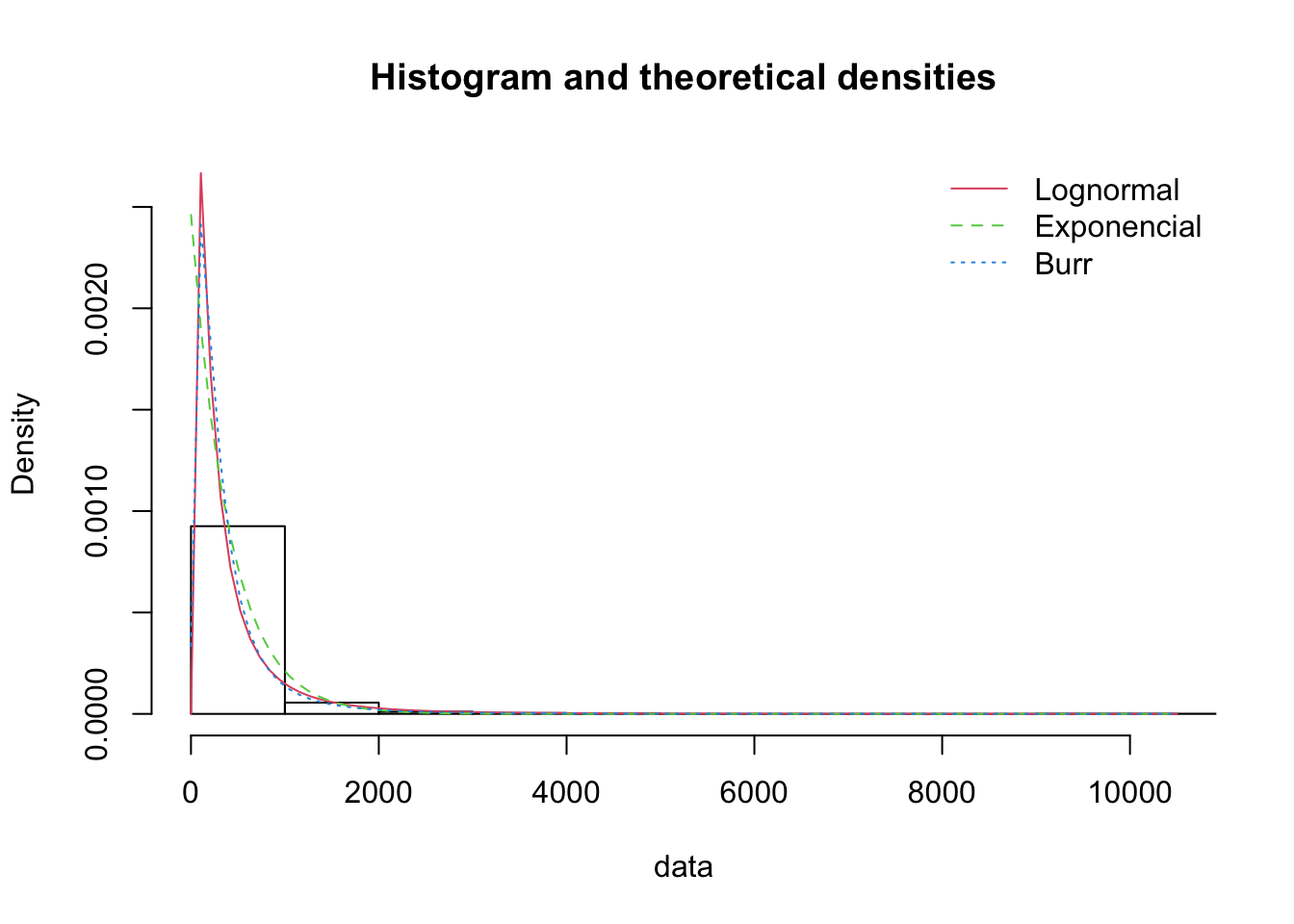
3.6 Ajuste de distribuciones a datos históricos de pérdidas
Cuando ajustamos una distribución a un conjunto de datos, es importante evaluar qué tan bien se ajusta el modelo. Los paquetes como fitdistrplus en R permiten realizar esta tarea y proporcionan estadísticos de bondad de ajuste, entre los más comunes:
- Kolmogorov-Smirnov (KS)
- Cramér-von Mises (CvM)
- Anderson-Darling (AD)
Estas pruebas comparan la distribución empírica (la que proviene de los datos) con la distribución teórica (la que ajustamos), pero cada una tiene distintos enfoques.
3.6.1 Kolmogorov-Smirnov (KS)
El estadístico KS se define como:
\[ D_n = \sup_x | F_n(x) - F(x) | \]
Donde:
- \(F_n(x)\) es la función de distribución empírica (EDF)
- \(F(x)\) es la función de distribución acumulada teórica (CDF)
- \(\sup\) indica el máximo absoluto en todo el dominio de los datos
Es decir, mide la máxima diferencia entre las curvas de distribución empírica y teórica.
## Cargar librerías
library(fitdistrplus)
# Simular datos y ajustar una normal
set.seed(123)
# x <- rweibull(100, shape = 2, scale = 1)
# x <- rnorm(100)
x <- stats::rexp(500,rate = 1/3)
ajuste <- fitdist(x, "norm")
# Funciones útiles
Fn <- ecdf(x)
F_theo <- function(t) pnorm(t, mean = ajuste$estimate["mean"], sd = ajuste$estimate["sd"])
x_vals <- sort(x)
n <- length(x_vals)
## Kolmogorov-Smirnov
ks_stat <- max(abs(Fn(x_vals) - F_theo(x_vals)))
## Mostrar valores
cat("Estadísticos calculados:\n")## Estadísticos calculados:## Kolmogorov-Smirnov (KS): 0.14131## Gráfica de Kolmogorov-Smirnov
plot(Fn, verticals = TRUE, col = "blue", main = "Kolmogorov-Smirnov: Máxima diferencia", xlab = "x", ylab = "Distribución acumulada")
lines(x_vals, F_theo(x_vals), col = "red", lwd = 2)
x_max <- x_vals[which.max(abs(Fn(x_vals) - F_theo(x_vals)))]
segments(x_max, Fn(x_max), x_max, F_theo(x_max), col = "darkgreen", lwd = 2, lty = 2)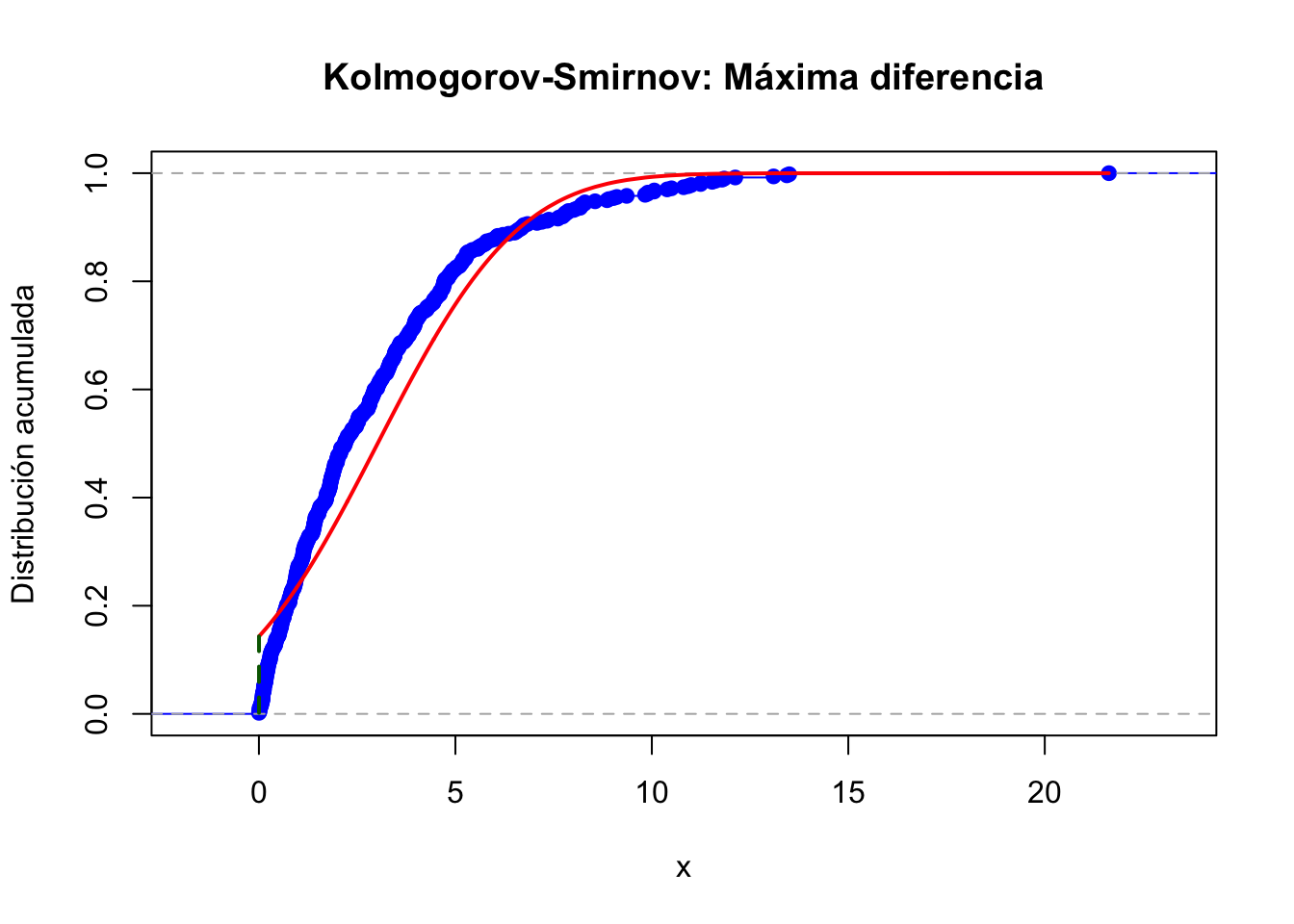
3.6.2 Cramér-von Mises (CvM)
El estadístico CvM es una medida integrada (área) de discrepancia entre las dos distribuciones:
\[ W^2 = n \int_{-\infty}^{\infty} \left[F_n(x) - F(x)\right]^2 dF(x) \]
Una versión computacional, usando los valores ordenados \(x_{(i)}\), es:
\[ W^2 = \frac{1}{12n} + \sum_{i=1}^{n} \left( F(x_{(i)}) - \frac{2i - 1}{2n} \right)^2 \]
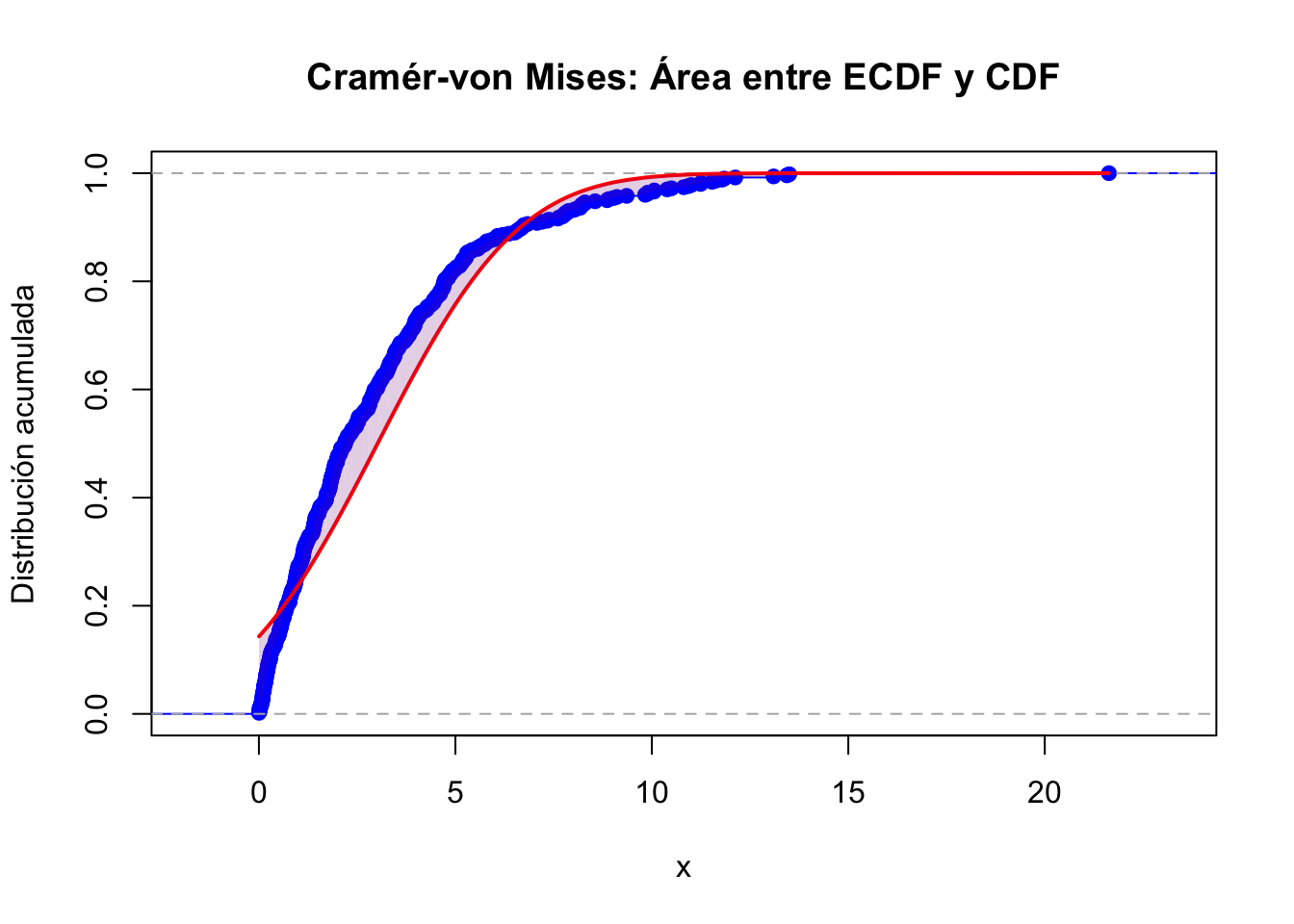
A diferencia del KS, considera toda la curva, no solo el punto de mayor discrepancia.
## Cramér-von Mises
u_i <- (2 * (1:n) - 1) / (2 * n)
F_vals <- F_theo(x_vals)
cvm_stat <- (1 / (12 * n)) + sum((F_vals - u_i)^2)
## Mostrar valores
cat("Estadísticos calculados:\n")## Estadísticos calculados:## Cramér-von Mises (CvM): 3.00253## Gráfica de Cramér-von Mises (área entre curvas)
plot(Fn, verticals = TRUE, col = "blue", main = "Cramér-von Mises: Área entre ECDF y CDF", xlab = "x", ylab = "Distribución acumulada")
lines(x_vals, F_theo(x_vals), col = "red", lwd = 2)
for (i in seq_along(x_vals[-1])) {
x0 <- x_vals[i]
x1 <- x_vals[i + 1]
polygon(c(x0, x0, x1, x1), c(Fn(x0), F_theo(x0), F_theo(x1), Fn(x1)),
col = rgb(0.5, 0, 0.5, alpha = 0.2), border = NA)
}
3.6.3 Anderson-Darling (AD)
El estadístico AD también mide la diferencia global, pero da mayor peso a los extremos (colas):
\[ A^2 = -n - \frac{1}{n} \sum_{i=1}^{n} \left[ (2i - 1) \left( \log F(x_{(i)}) + \log(1 - F(x_{(n+1-i)})) \right) \right] \]
Esto es útil cuando queremos detectar desviaciones en las colas (muy altas o muy bajas).
## Anderson-Darling
log_terms <- log(F_vals) + log(1 - rev(F_vals))
ad_stat <- -n - (1/n) * sum((2 * (1:n) - 1) * log_terms)
## Mostrar valores
cat("Estadísticos calculados:\n")## Estadísticos calculados:## Anderson-Darling (AD): 18.73001## Gráfica de pesos en AD
# Recalcular para seguridad
F_vals <- F_theo(x_vals)
weights_ad <- 1 / (F_vals * (1 - F_vals))
diffs_ad <- abs(F_vals - Fn(x_vals))
# Normalizar pesos a [0, 1] para visualización
scaled_weights <- (weights_ad - min(weights_ad)) / (max(weights_ad) - min(weights_ad))
# Gráfico base
plot(Fn, verticals = TRUE, col = "blue", pch = 19, cex = 0.5,
main = "Anderson-Darling: Diferencias ponderadas por peso",
xlab = "x", ylab = "Distribución acumulada", xlim = range(x_vals))
lines(x_vals, F_vals, col = "red", lwd = 2)
# Dibujar líneas verticales con grosor y color según el peso
for (i in seq_along(x_vals)) {
x0 <- x_vals[i]
y_emp <- Fn(x0)
y_teo <- F_vals[i]
w <- scaled_weights[i]
col_opacity <- rgb(0.5, 0, 0.5, alpha = 0.3 + 0.7*w) # más opaco si mayor peso
segments(x0, y_emp, x0, y_teo, col = col_opacity, lwd = 2 + 10*w)
}
# Añadir puntos para marcar ECDF y CDF
# points(x_vals, Fn(x_vals), pch = 1, col = "blue", cex = 0.6)
# points(x_vals, F_vals, pch = 3, col = "red", cex = 0.6)
legend("bottomright",
legend = c("ECDF", "CDF Teórica", "Diferencias ponderadas"),
col = c("blue", "red", rgb(0.5, 0, 0.5)),
lty = c(NA, NA, 1), pch = c(1, 3, NA), lwd = c(NA, NA, 3),
pt.cex = c(0.8, 0.8, NA))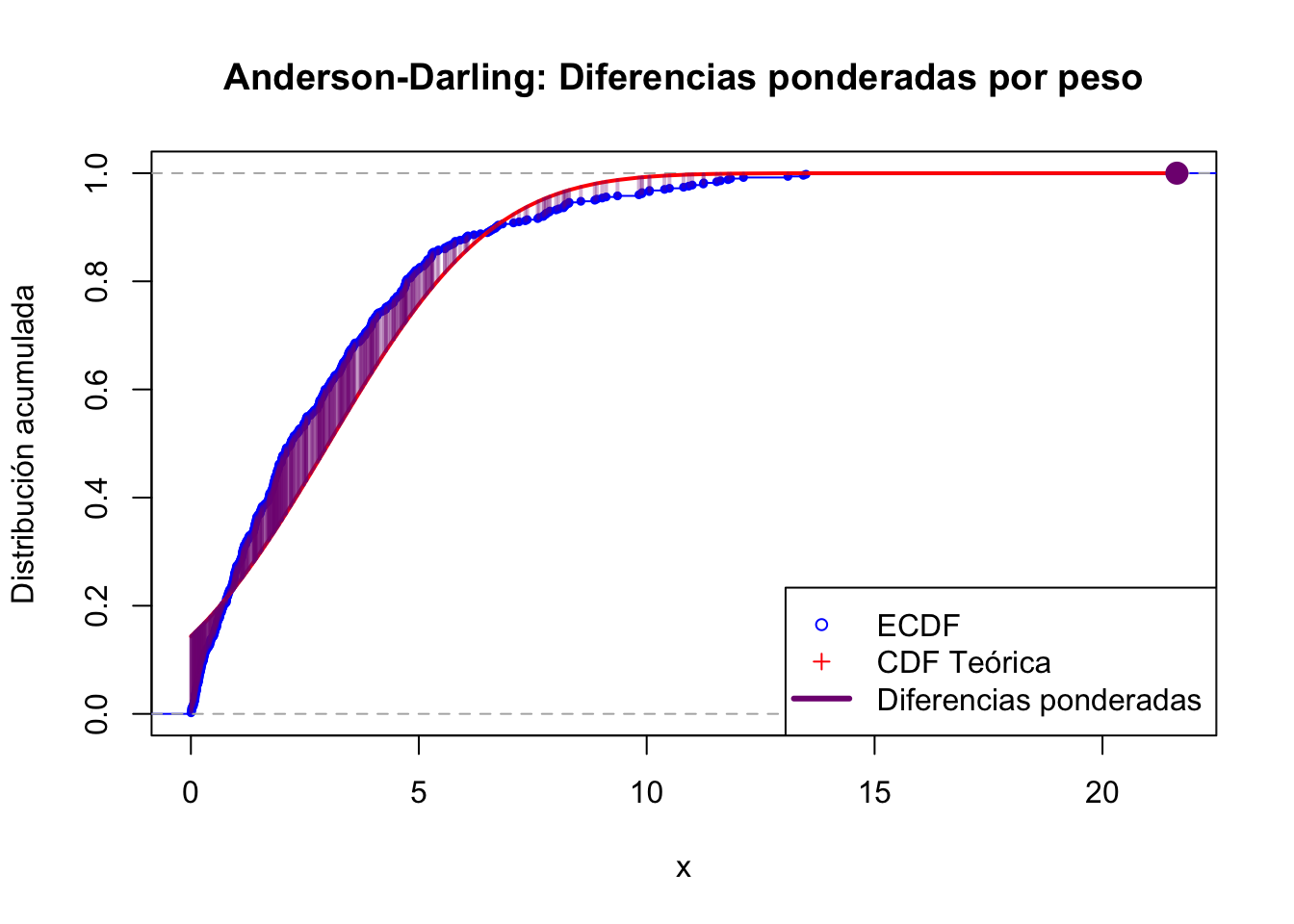
3.6.6 Bondad de ajuste
## Goodness-of-fit statistics
## 1-mle-lnorm 2-mle-exp 3-mle-burr
## Kolmogorov-Smirnov statistic 0.03546962 0.0734378 0.01511828
## Cramer-von Mises statistic 0.36876808 2.0731848 0.03504477
## Anderson-Darling statistic 2.50198990 11.3420563 0.22644142
##
## Goodness-of-fit criteria
## 1-mle-lnorm 2-mle-exp 3-mle-burr
## Akaike's Information Criterion 15545.53 15640.53 15490.52
## Bayesian Information Criterion 15555.57 15645.55 15505.57Interpretación
- La lognormal capta adecuadamente la masa central de los datos
- La exponencial subestima eventos extremos
- La Burr puede sobreajustar colas si hay pocos extremos
Conclusiones
- Modelar adecuadamente la severidad permite estimar correctamente medidas como Expected Loss o Value-at-Risk
- Las distribuciones deben seleccionarse con base en evidencia empírica y criterios de validación (AIC, gráficos, ajuste visual)
- El uso de distribuciones con colas pesadas es esencial en entornos con posibles eventos extremos
Referencias
- Basel Committee on Banking Supervision (2006). International Convergence of Capital Measurement and Capital Standards – A Revised Framework (Comprehensive Version). BCBS 128.
- Klugman, S. A., Panjer, H. H., & Willmot, G. E. (2012). Loss Models: From Data to Decisions. Wiley.
- McNeil, A. J., Frey, R., & Embrechts, P. (2015). Quantitative Risk Management. Princeton University Press.
- Embrechts, P., Klüppelberg, C., & Mikosch, T. (1997). Modelling Extremal Events for Insurance and Finance. Springer.