3.4 Distribuciones aplicadas a la severidad de pérdidas

3.4.1 Normal

Fórmula densidad:

\[ f(x; \mu, \sigma) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x - \mu)^2}{2\sigma^2}} \]

Parámetros:

  • \(\mu\): media

  • \(\sigma\): desviación estándar

Uso: sólo en casos donde las pérdidas son simétricas o para fines pedagógicos. No se usa típicamente en riesgo operacional porque permite valores negativos.

Ejemplo:

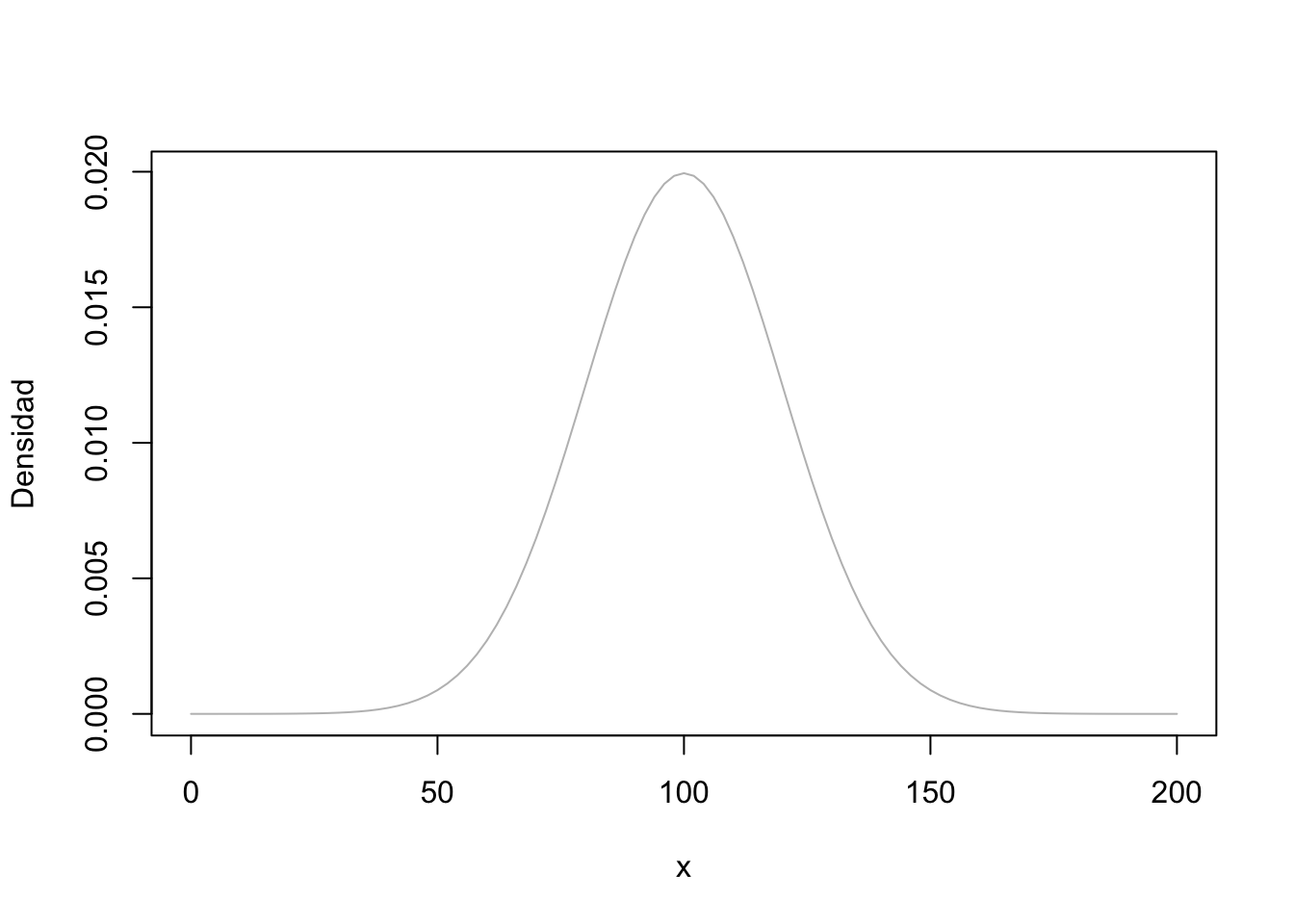
curve(dnorm(x, mean = 100, sd = 20), from = 0, to = 200, col = "gray", ylab = "Densidad")

3.4.2 Lognormal

Fórmula densidad: \[ f(x; \mu, \sigma) = \frac{1}{x\sigma\sqrt{2\pi}} e^{-\frac{(\ln x - \mu)^2}{2\sigma^2}} \]

Parámetros:

  • \(\mu\): media de \(\ln(X)\)

  • \(\sigma\): desviación estándar de \(\ln(X)\)

Uso: ideal para modelar pérdidas con alta asimetría positiva. Muy usada en riesgo operacional y de seguros.

Ejemplo:

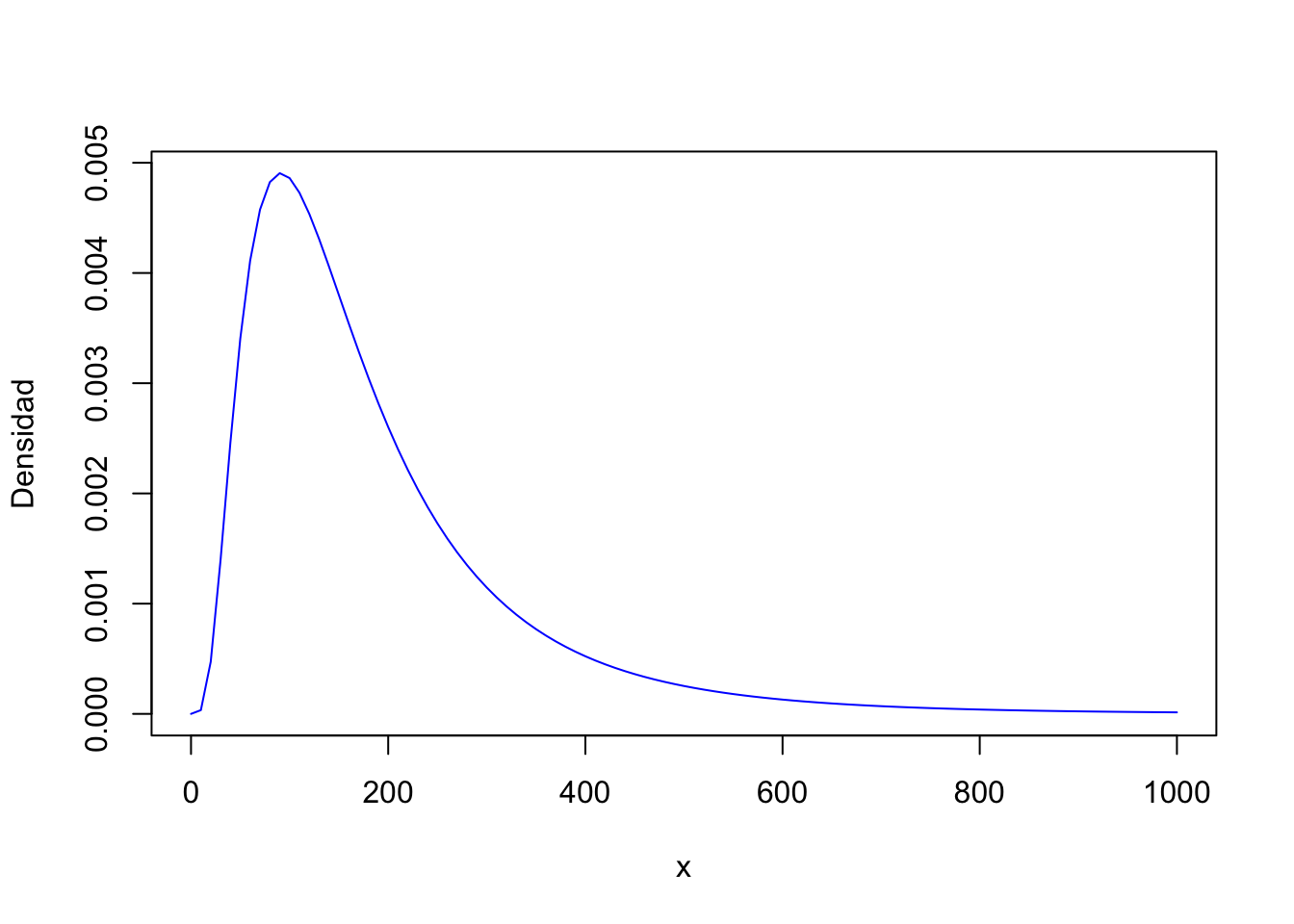
curve(dlnorm(x, meanlog = 5, sdlog = 0.7), from = 0, to = 1000, col = "blue", ylab = "Densidad")

3.4.3 Exponencial

Fórmula densidad:

\[ f(x; \lambda) = \lambda e^{-\lambda x} \]

Parámetros:

  • \(\lambda\): tasa de decaimiento

Uso: útil para pérdidas pequeñas frecuentes. No adecuada para colas pesadas.

Ejemplo:

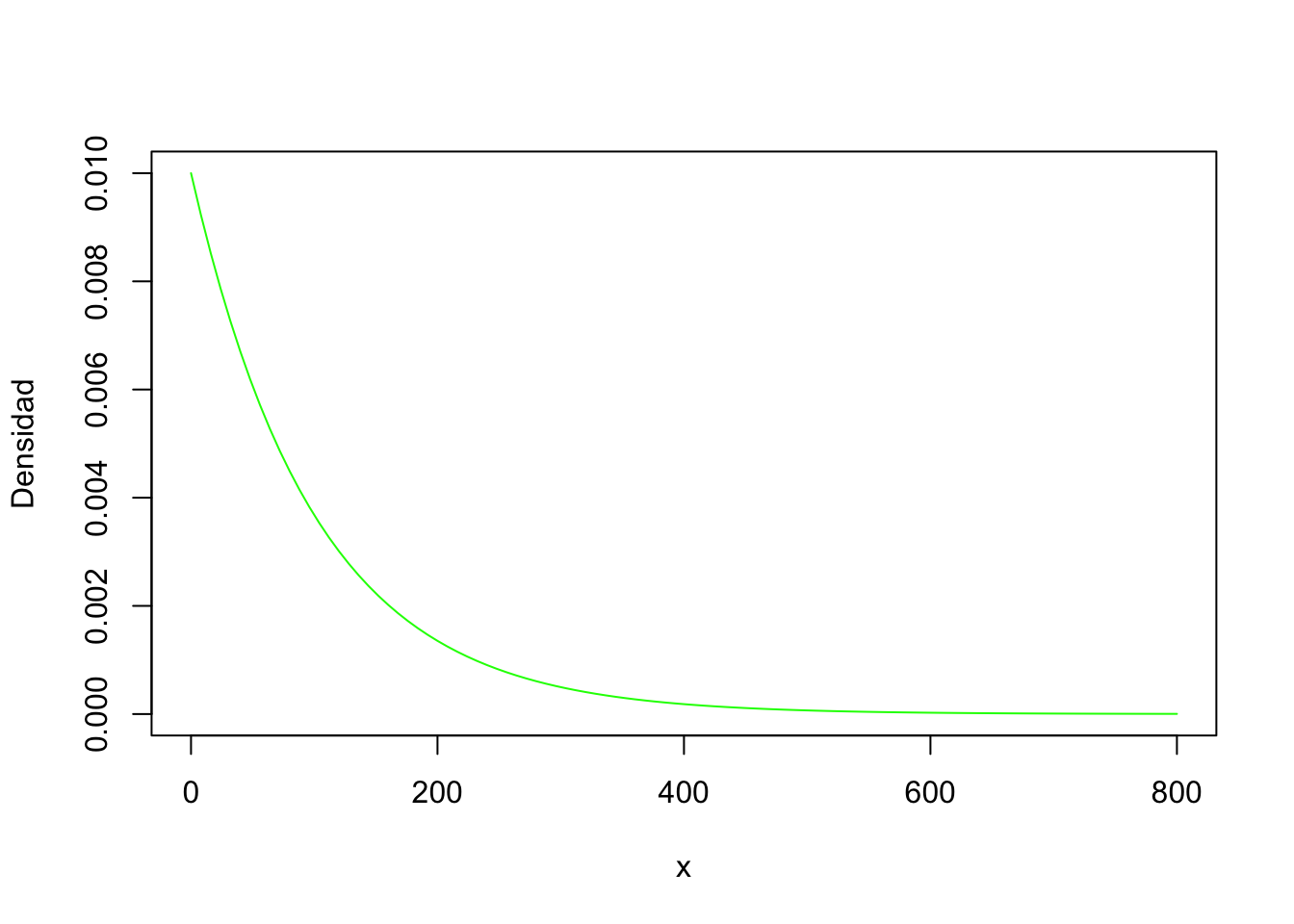
curve(dexp(x, rate = 1/100), from = 0, to = 800, col = "green", ylab = "Densidad")

3.4.4 Burr (Tipo XII)

Fórmula densidad: \[ f(x; c, k) = \frac{ckx^{c-1}}{(1 + x^c)^{k+1}} \]

Parámetros:

  • \(c\): parámetro de forma

  • \(k\): parámetro de cola

  • A menudo usada con escala \(\theta\) como \(f(x/\theta) / \theta\)

Uso: muy flexible para modelar pérdidas con colas pesadas y extremos.

Ejemplo:

curve(dburr(x, shape1 = 2, shape2 = 3, rate = 1/800), from = 0, to = 3000, col = "purple", ylab = "Densidad")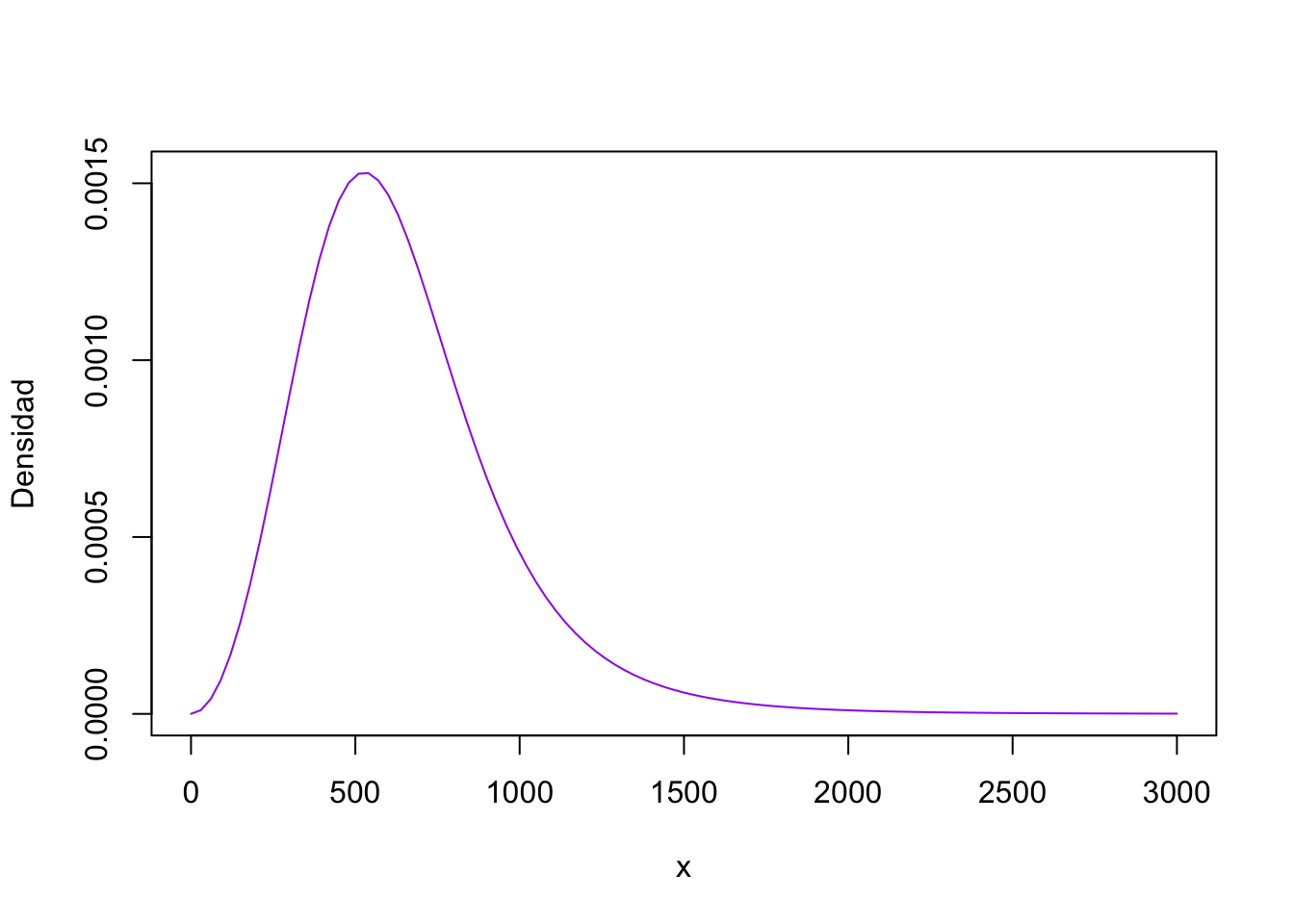

3.4.5 Comparación de propiedades estadísticas

Distribución Soporte Asimetría Cola pesada Valores negativos Uso en riesgo operacional
Normal \(\mathbb{R}\) Baja No Sí No recomendada
Lognormal \((0, \infty)\) Alta Moderada No Muy usada
Exponencial \((0, \infty)\) Media Ligera No Aceptable en ciertos casos
Burr XII \((0, \infty)\) Alta Alta No Muy útil para extremos

3.4.6 Ejercicios

  1. Calcular la media y varianza de una variable con distribución lognormal(\(\mu = 8, \sigma = 1\)) usando las fórmulas teóricas.
  2. Simular 1.000 observaciones de cada distribución y comparar sus histogramas.
  3. Ajustar una distribución Burr a un subconjunto de losses y comparar con la lognormal.
  4. Discutir: ¿cuál distribución usaría en un escenario con alto riesgo cibernético?

Puedes usar rlnorm, rexp y rburr para simular datos y fitdist() para ajustar modelos.